Consider the function [[$ f (x) = x + 3 $]]. The function is a first-degree polynomial function that creates the graph [[$ y = x + 3 $]]. Do you still remember how to draw a line using the solved form of the equation?

The constant term [[$ b $]] indicates the point at which the line intersects the [[$ y $]]-axis. Therefore, it is the [[$ y $]]-coordinate of the intersection point between the line and the [[$ y $]]-axis. The second point through which the line passes can be determined by using the line's slope. The slope of a line tells you how much the [[$ y $]]-coordinate changes (increases or decreases) as the [[$ x $]]-coordinate increases by one. In the coordinate system, move from the intersection of the [[$ y $]]-axis to the number indicated by slope's denominator along the [[$ x $]]-axis and to the number indicated by the slope's numerator along the [[$ y $]]-axis.

Correspondingly, the equation of the line and the function it describes can be determined on the basis of a linear graph. The constant term of the equation of the line [[$ y = kx + b $]] is seen from the intersection of the graph and the [[$ y $]]-axis. The slope can be calculated by using two points on the line. Its value is independent of the selected points.

The graph of a first-degree polynomial function is always an ascending or descending line. Because of this, first-degree functions are called linear functions. The higher the absolute value of the slope, the bigger the decrease and decrease of the function.

If the slope is zero, [[$ x $]] disappears completely from the function equation. When this happens, the value of the function does not depend in any way on the value of the variable [[$ x $]]. Such a function is called a zero-degree polynomial function or a constant function.

Example 1

Draw a graph for the function [[$ f(x) = -2x + 3 $]]​.

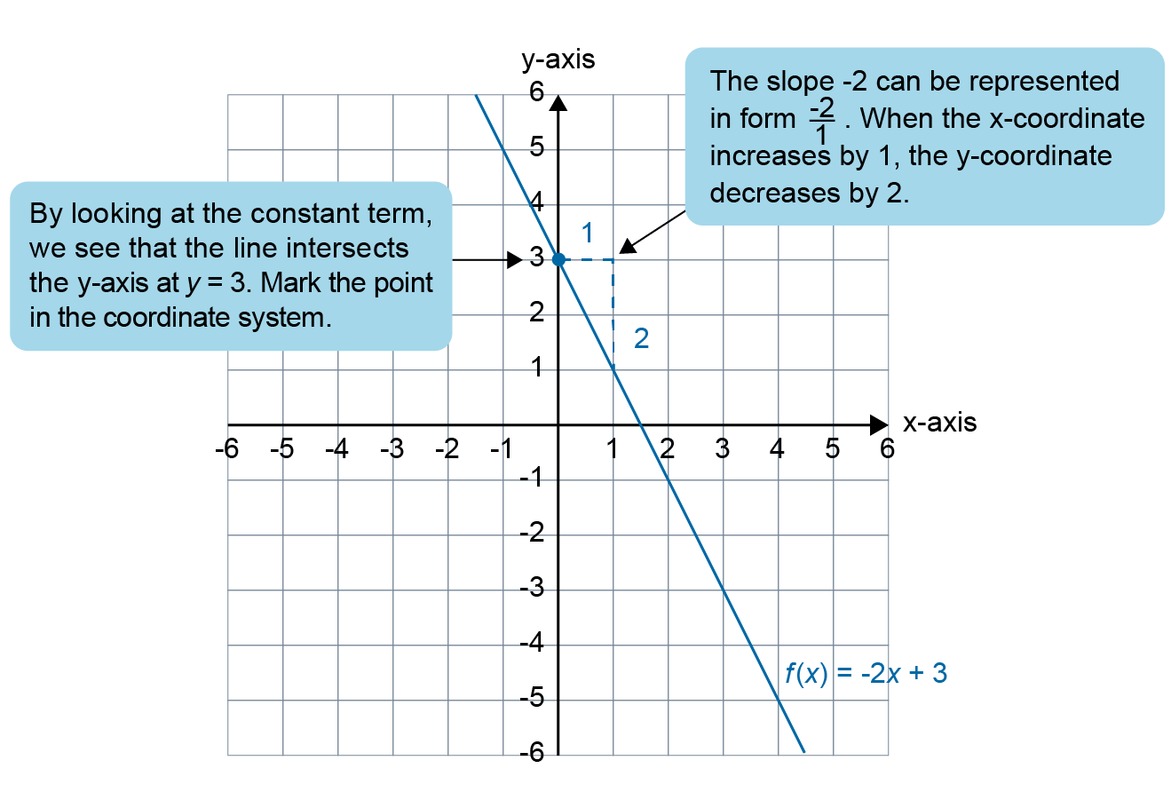
Example 2

Form a function that describes the price charged for the work at a car repair shop in relation to time spent. Use the function to calculate how much a five-hour repair job costs.

Mark the time with [[$ x $]] and the price with [[$ y $]]. The equation of the line is of the form [[$ y = kx + b $]]. In order to form an equation corresponding to the graph, we need to solve and place the slope and the constant term in the equation of the line.

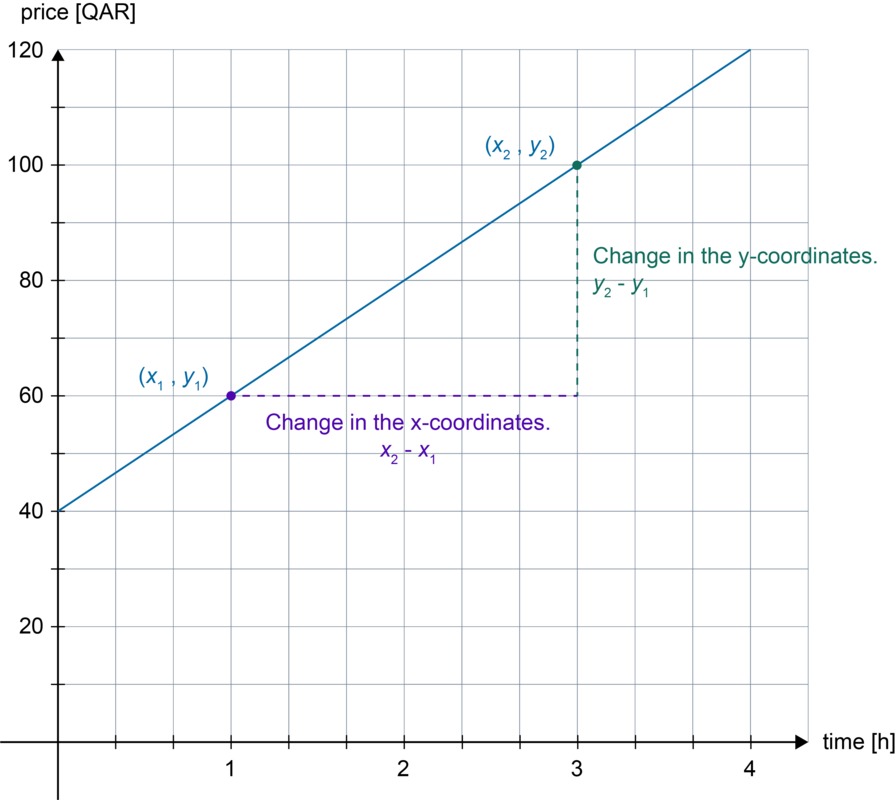
The constant [[$ b $]] is obtained from the intersection of the line and the [[$ y $]]-axis, i.e. [[$ b = 40 $]].

Select [[$ (x_1, y_1) = (1, 60) $]] and [[$ (x_2, y_2) = (3, 100) $]] as the viewpoints from which the slope is calculated. 

[[$ k = \displaystyle\frac {y_2 - y_1} {x_2 - x_1} = \displaystyle\frac {100 - 60} {3 - 1} = \displaystyle\frac {40} {2} = 20 $]]​

Place the slope and the constant in the line equation to obtain [[$ y = 20x + 40 $]]. This means that the price function is [[$ f (x) = 20x + 40 $]].

The value of the function when [[$ x $]]'s value is [[$ 5 $]] can be calculated as [[$ f (5) = 20 \cdot 5 + 40 = 140 $]].

Answer: The price is determined from the function [[$ f (x) = 20x + 40 $]], where [[$ x $]] is the working time in hours. The price of a five-hour repair job is therefore [[$ 140 $]] QAR.