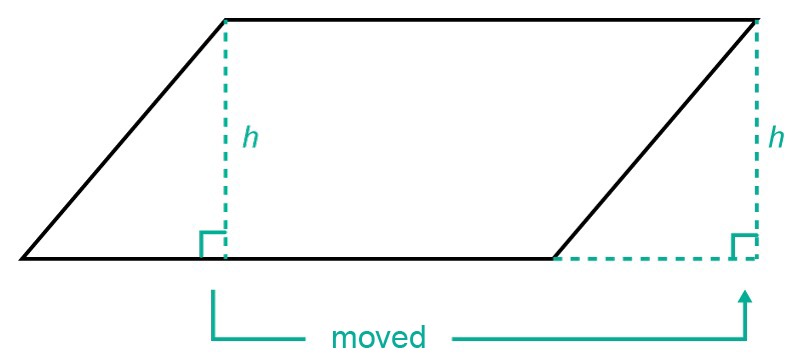
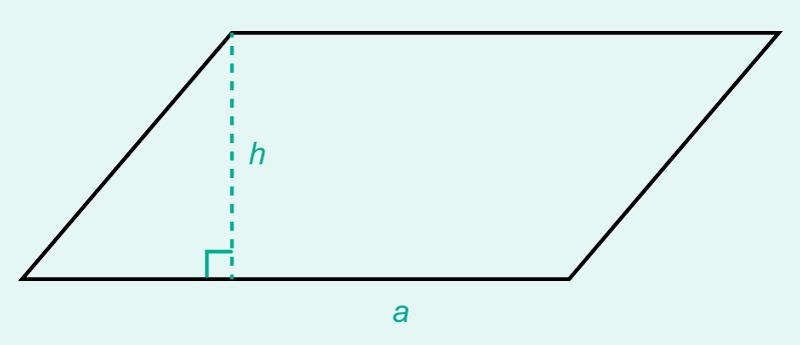
A parallelogram can be formed from a rectangle by cutting a rectangular triangle off the edge of the rectangle and moving it to the opposite edge of the rectangle. Thus, the rectangle and the parallelogram are formed from the same parts. This means that they also must have the same area.

The area of a parallelogram is the product of its base and its altitude:

[[$ A = a \cdot h $]]

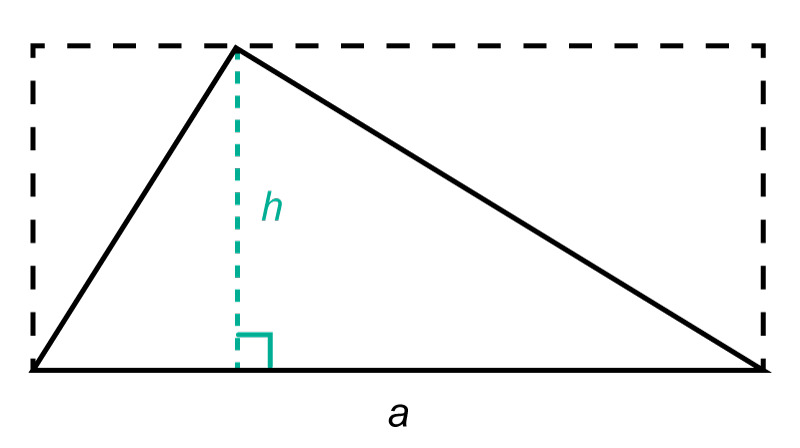
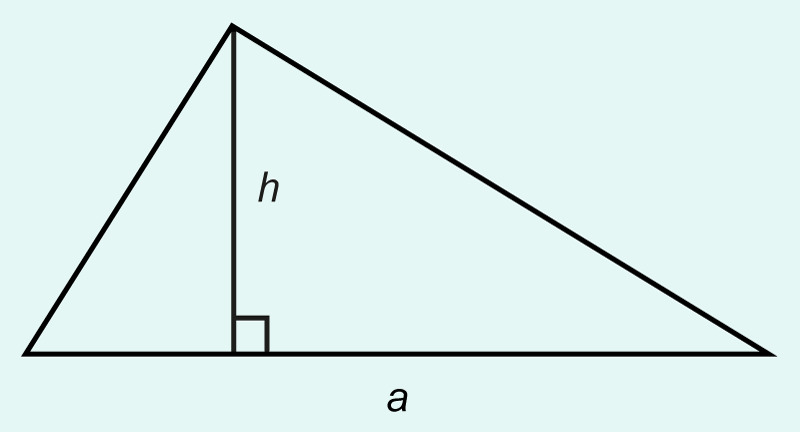
A triangle can be completed into a rectangle according to the dotted lines displayed in the adjacent image. When converting a triangle into the rectangle, the added triangles form an area that is equal in size with the original triangle. Therefore, the area of a triangle is obtained by calculating the area of a rectangle and dividing it by two.

The area of a triangle is the product of its base and its altitude divided by two:

[[$ A = \dfrac{a \cdot h}{2}$]]

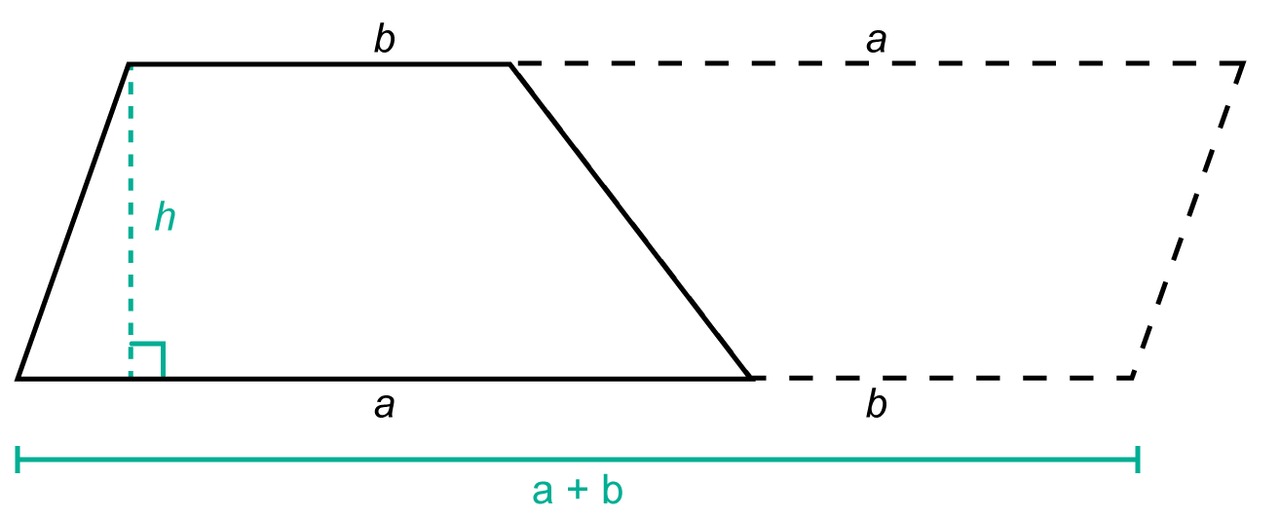
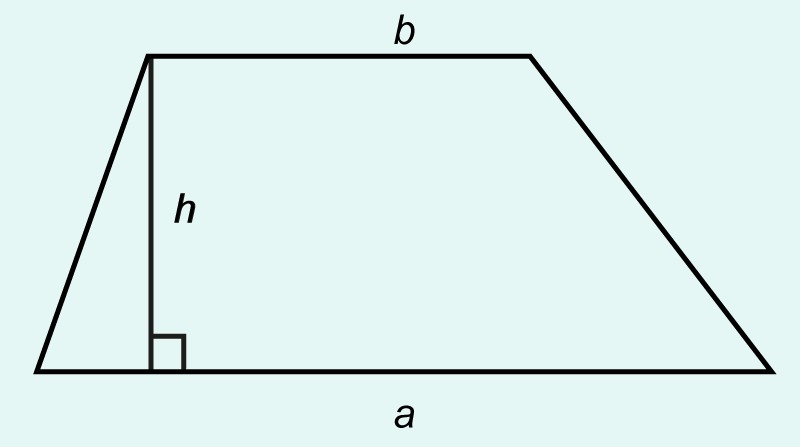
A parallelogram can be formed from two trapeziums of the same size. The height of the parallelogram is the height h of the trapezium, and the sum of the bases of the trapezium is [[$ a + b $]].

The area of the trapezium is obtained by dividing the area of the formed parallelogram by two.

The area of a trapezium is the product of the mean of its bases and its altitude:

[[$ A = \dfrac{a+b}{2} \cdot h $]]

The areas of all other polygons can be calculated by dividing the polygon into triangles or quadrilaterals and adding their areas together. In all area calculations, care must be taken to ensure that each dimension is placed in the calculation formula in the same unit.

Examples

Example 1

Calculate the area of the parallelogram.

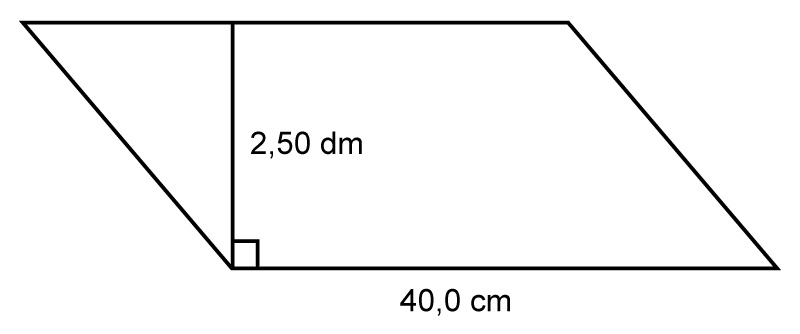Before placing the dimensions in the formula, they must be converted into the same unit. The decimeters must therefore be converted into centimeters.

[[$ \text{2.50 dm} = \text{25.0 cm}$]].

[[$ A = a \cdot h = \text{40.0 cm} \cdot \text{25.0 cm} = 1 000 \text{ cm}^2 $]]

Answer: The area of the parallelogram is [[$ 1 000 \text{ cm}^2$]].

Example 2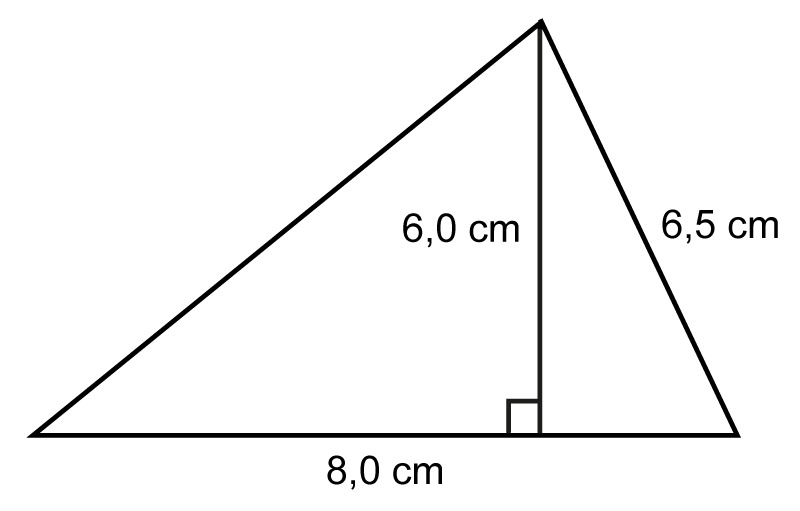

Calculate the area of the triangle.

The length of the triangle's side is given in the problem, but it is not needed to calculate the area.

[[$ A = \dfrac{a \cdot h}{2} = \dfrac{\text{8.0 cm} \cdot \text{6.0 cm}}{2} = \dfrac{48 \text{ cm}^2}{2} = 24 \text{ cm}^2 $]]

Answer: The area of the triangle is [[$ 24 \text{ cm}^2$]].

Note! In parallelograms, triangles and trapeziums, the altitude of the figure is different from its side lengths. Because of this, the side lengths cannot be used to calculate the areas of these figures.

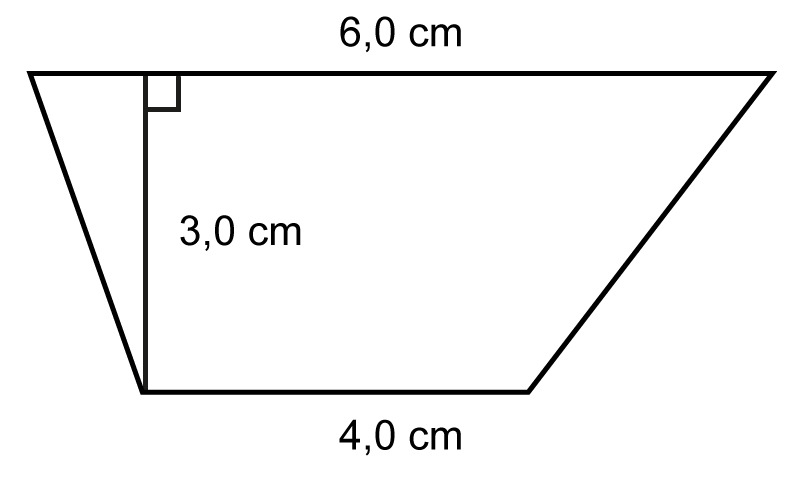
Example 3

Calculate the area of the trapezium when its bases are [[$\text{4,0}$]] cm and [[$\text{6.0}$]] cm long and the distance between them is [[$\text{3.0}$]] cm.

It is a good idea to start solving the verbal problems of geometry by drawing a picture of the situation, marking all the given dimensions.

Place the values in the trapezium area formula:

[[$ A = \dfrac{a + b}{2} \cdot h = \dfrac{\text{4.0 cm} + \text{6.0 cm}}{2} \cdot \text{3.0 cm}= \dfrac{\text{ 10.0 cm}}{2} \cdot \text{3.0 cm} = 5 \text{ cm} \cdot \text{3.0 cm} = \text{15 cm}^2$]]

Answer: The trapezium has an area of [[$ 15 \text{ cm}^2$]].