12. Solving a pair of inequalities*
Solving a pair of inequalities
Inequalities can also be viewed in pairs. In a pair of inequalities, attention should be paid to whether both inequalities must be valid simultaneously, or whether it is sufficient that even one of the inequalities holds.
Solving a pair of inequalities
Pairs of inequalities are solved by first solving both inequalities separately. The Boolean operator that occurs in the pair of inequalities determines how their solutions must be combined.If the word
- "and" appears in a pair of inequalities, both inequalities must be true simultaneously
- "or" appears in a pair of inequalities, it is sufficient that one of the inequalities is true.
Example 1
Which values of [[$ x $]] implement the pairs of inequalities?
a)
[[$ \begin{equation} \left \{ \begin{aligned} x + 5\! &≥ 7 \\ \text {and} \\ 2x - 1\! &< 13 \\ \end{aligned} \right. \end{equation} $]]Initially, both inequalities are solved separately.
[[$ \begin{align*}
x + 5\! &≥ 7 \\
x \!&≥ 7 - 5 \\
x\! &≥ 2 \\
\end{align*} $]]
[[$ \begin{align*} 2x - 1 \! &< 13 \\ 2x \! &< 13 + 1 \; \; \; \; \; \; || \; :2 \\ x \! &< \displaystyle\frac {14} {2} \\ x \! &< 7 \\ \end{align*} $]]
Let us use a number line to find the area where both inequalities are true.

Answer: [[$ 2 ≤ x < 7 $]]
b)
[[$ \begin{equation}
\left \{
\begin{aligned}
3 - x\! &> 0 \\
\text {or} \\
x + 3\! &≥ 9 \\
\end{aligned} \right.
\end{equation}
$]]
Initially, both inequalities are solved separately.
[[$ \begin{align*} 3 - x \! &> 0 \\ -x \!&> - 3 \;\;\;\;\;\; || \; :(-1) \\ x\! &< 3 \;\;\;\;\;\;\;\; {\color {blue} {\text {The direction of the inequality sign changes!}}} \\ \end{align*} $]]
or[[$ \begin{align*} x + 3 \! &≥ 9 \\ x \! &≥ 9 - 3 \\ x \! &≥ 6 \\ \end{align*} $]]
Let us use a number line to find the area where even one of the inequalities is true.
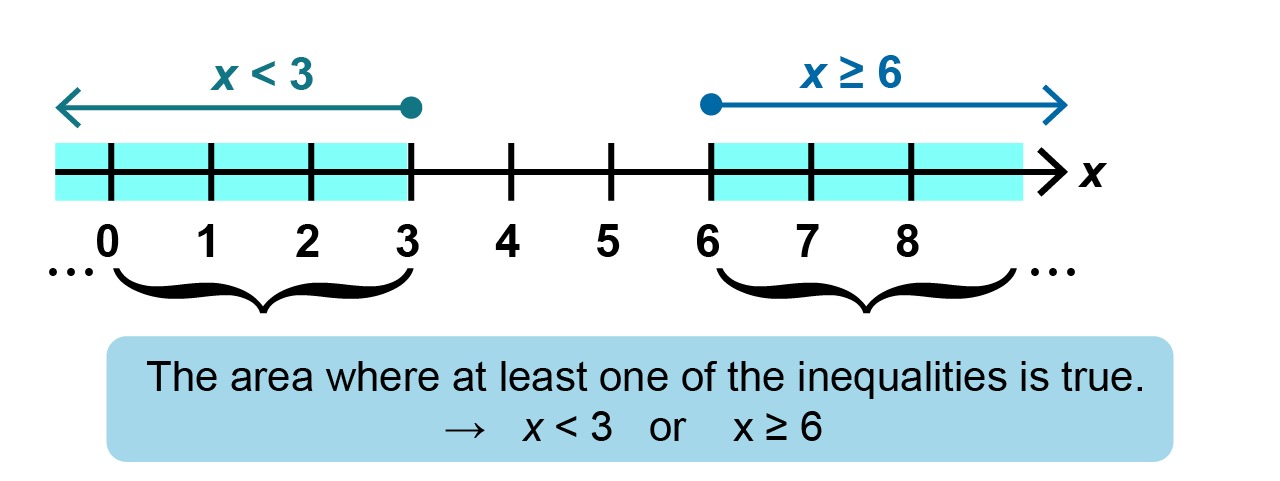
Answer: [[$ x < 3 $]] or [[$ x ≥ 6 $]]
Note! The notation [[$ 2 ≤ x <7 $]] is called a double inequality, because it contains two inequality signs. If two inequalities have to be realized at the same time, the pair of inequalities is usually written as a double inequality.
Inequalities with only one variable are easiest to illustrate with a number line. However, the inequalities of the two variables can also be examined in the coordinate system. Let's look the areas into which the line [[$ y = x $]] divides the [[$ xy $]] coordinate system.
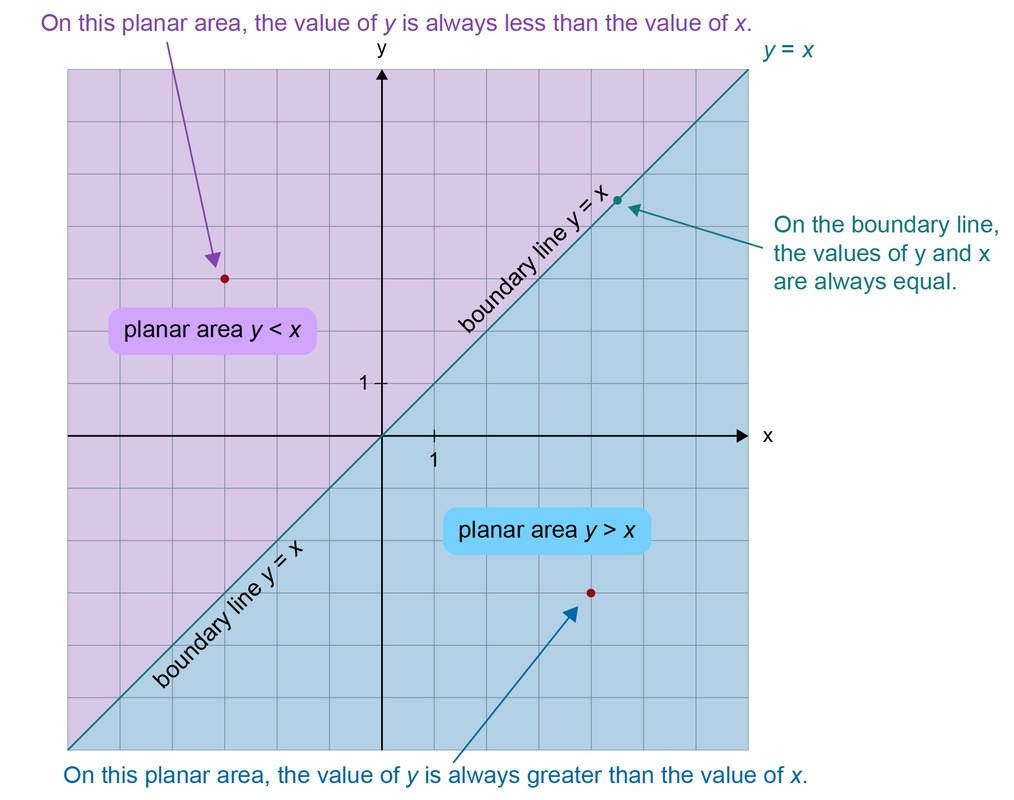
The easiest way to find planar areas formed by more than one boundary line is to experiment. In this case, an observation point is selected from each planar area. It is then examined which of the points satisfies both inequalities.
Example 2
In which planar area are the points that satisfy the inequalities [[$ y> 2x - 4 $]] and [[$ x ≥ 1 $]] located?
Solution:
The boundary lines of the coordinate system are [[$ y = 2x - 4 $]] and [[$ x = 1 $]], which divide the [[$ xy $]] plane into four planar areas. The boundary line [[$ y = 2x - 4 $]] is drawn with dashed lines, because its points no longer meet the required inequality. Select observation points from each planar area and place them in both inequalities. By doing so, you can examine which of the points satisfies both inequalities.
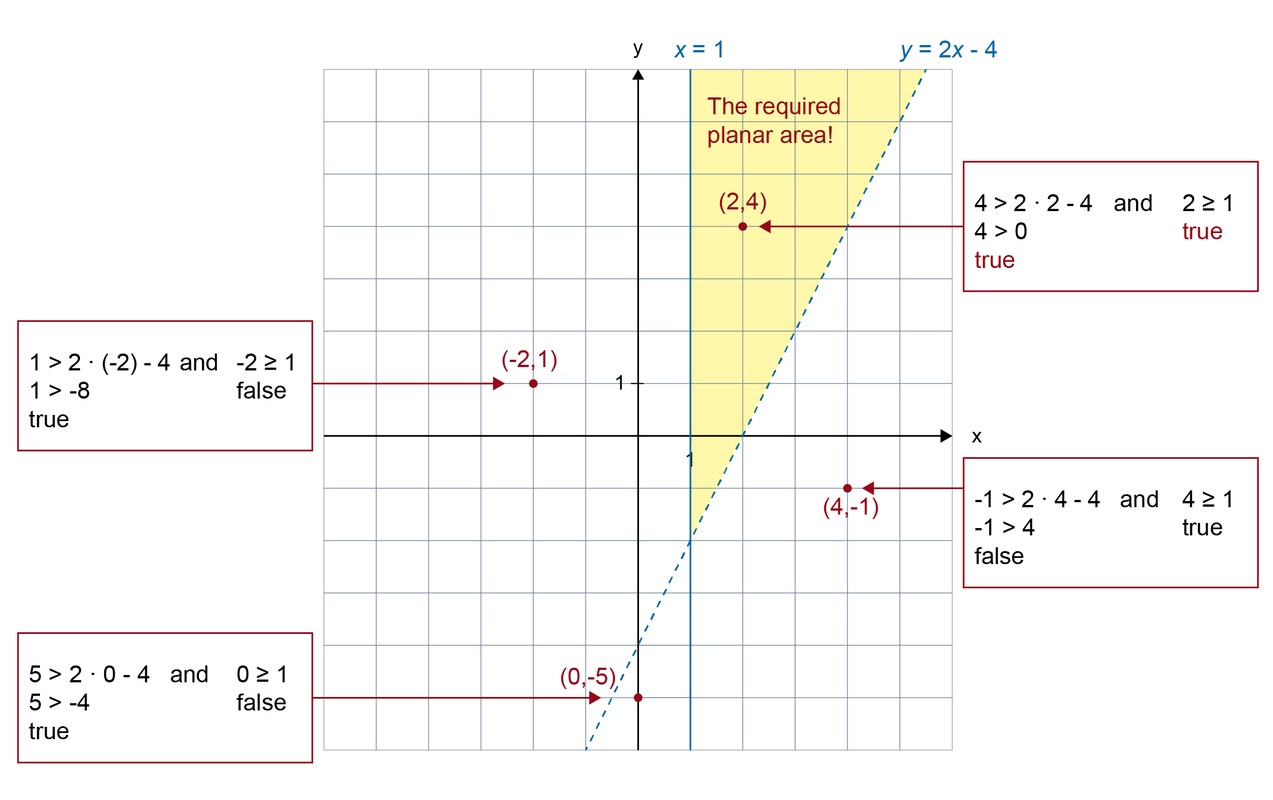
The viewpoint [[$ (2, 4) $]] implements both inequalities, which means that the requested planar area is where this point is located.
Note! Considerations of the realization of inequalities could have been stopped after the point [[$ (2, 4) $]], because there can be only one level range that implements both inequalities simultaneously. However, it is a good idea to examine all review points to detect a possible error.
Exercises
Basic exercises
1/15. Exercise 15.01
1/15. Exercise 15.02
1/15. Exercise 15.03
1/15. Exercise 15.04
1/15. Exercise 15.05
1/15. Exercise 15.06
1/15. Exercise 15.07
1/15. Exercise 15.08
1/15. Exercise 15.09
1/15. Exercise 15.10
1/15 Exercise 15.11
1/15. Exercise 15.12
1/15. Exercise 15.13
1/15. Exercise 15.14
1/15. Exercise 15.15
1/15. Exercise 15.16
1/15. Exercise 15.17
1/15. Exercise 15.18
1/15. Exercise 15.19
1/15. Exercise 15.20
1/15. Submission folder for answers
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.