20. Inverse proportion

Inverse proportionality

Walking a complete lap around a fitness trail at a speed of [[$ 5 $]] km/h takes [[$ 30 $]] minutes. However, running through the same trail at a speed of [[$ 10 $]] km/h takes [[$ 15 $]] minutes. When the speed doubles, the time is halved. This is an example of inverse proportionality. Two quantities are inversely proportional, when their values change in the same proportion but in different directions.

Inverse proportionality

If the quantities [[$ x $]] and [[$ y $]] are inversely proportional, their number pairs [[$ (a, b) $]] and [[$ (c, d) $]] implement the following equation: [[$$ ab = cd $$]]

This can also be written in a different form, as follows:
[[$$ \displaystyle\frac {a} {c} = \displaystyle\frac {d} {b} $$]]

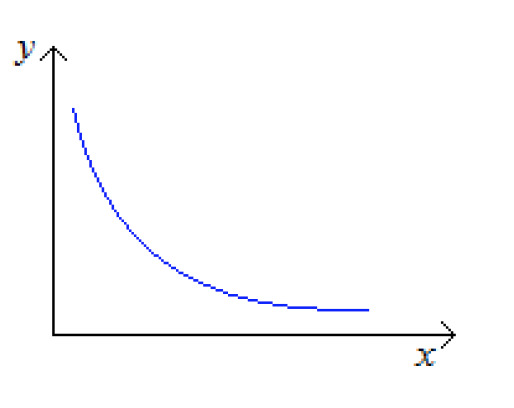
When the dependence of inversely proportional quantities is described in the coordinate system, the points lie on a curve called a hyperbel, as seen below.

Example 1

If a job takes four workers [[$ 6 $]] hours to finish, how much time does it take for three workers to finish the same job?

Solution:

Like direct proportionalities, inverse proportionalities can be utilized when solving proportional quantities. Mark the time it takes three workers to finish the job with [[$ x $]], and compile the set of numbers and times shown below.

The direction in which the amount of time it takes to finish the job increases must be deduced. Logically, the fewer workers there are to complete the job, the longer it will take them to finish it. Arrows that point in opposite directions indicate inversely proportional quantities. This layout can be turned into a proportion equation by “turning” the arrows so that they point in the same direction.
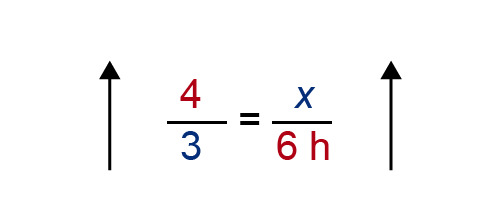By cross multiplying, we arrive at the following equation:

[[$ \quad \begin{align} 3 · x &= 4 · 6 \text{ h} \space ||:3 \ \\ x &= \dfrac{4 · 6 \text{ h}}{3} \ \\ x &= 8 \text{ h} \end{align} $]]

Answer: It takes [[$ 8 $]] h for three workers to finish the job.

Example 2

The speed of a plane was [[$ 600 $]] km/h on its first trip, which took [[$ 2.5 $]] hours. Due to headwinds, the plane travelled at a speed of [[$ 500 $]] km/h on the return trip. How long did the return trip take?

Solution:

Mark the time taken for the return journey with [[$ x $]] and set up a table of speeds and times.

Once again, as the quantities are inversely proportional, the direction of the arrows must be changed so that they point in the same direction.

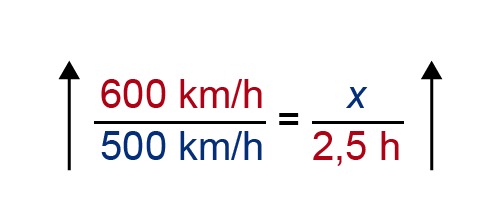
By cross multiplying, we arrive at the following equation:

[[$ \quad \require{cancel} \begin{align} 500 \text{ km/h} · x &= 600 \text{ km/h} · 2,5 \text{ h} \space ||:500 \text{ km/h} \ \\ x &= \dfrac{600 \cancel{\text{ km/h}} · 2,5 \text{ h}}{500 \cancel{\text{ km/h}}} \ \\ x &= 3 \text{ h} \end{align} $]]

Answer: The return trip took [[$ 3 $]] h.