At which value of [[$ x $]] does the function get a value of zero? At what point does the graph of the function intersect the [[$ x $]]-axis? Both of these questions are trying to find out the same thing, which is the x-intercept of a function. The x-intercept can be determined approximately by drawing. It is also easy to calculate.

Thus, the x-intercept of a function is determined by marking the expression of the function as equal to zero and solving this equation.

If the graph of the function is a line, it is said that the quantities [[$ x $]] and [[$ y $]] are linearly dependent on one another. Linear dependence describes a steady change in which the change per unit is equal during each step. A positive change means a linear increase, whereas a negative change means a linear decrease. If it is known that a phenomenon follows a linear model, and if two viewpoints are known, an equation of the model can be formed from the data.

Example 1

Solve the x-intercept of the function [[$ f (x) = x + 3 $]] a) by drawing and b) by calculating.

Solution:

a) [[$ f (x) = x + 3 $]] is a first-order polynomial function with a graph [[$ y = x + 3 $]]. Let's draw this in the coordinate system.

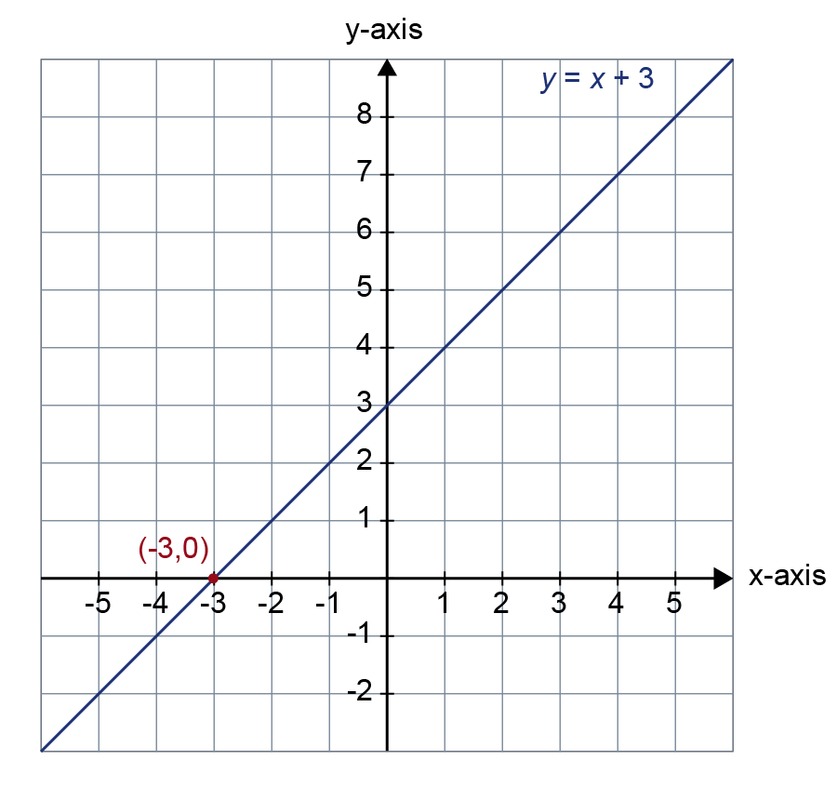
The zero is found at the intersection of the function graph and the [[$ x $]]-axis. It is [[$ x = -3 $]].

b) The x-intercept of the function satisfies the condition [[$ f (x) = 0 $]]. We can now solve the equation:

[[$ \begin{align*}x + 3 &= 0 \\x &= -3\end{align*} $]]​

Answer: [[$ x = -3 $]]​

Example 2

The base fare for a taxi is [[$ 4 $]] QAR. Each kilometer costs an extra [[$ 1,02 $]] QAR / km. Construct a function that represents the cost of a taxi ride as a function of the distance traveled, and plot it. What is the relationship between the distance and the price of a taxi ride?

Solution:

Enter the distance traveled with [[$ x $]] (in km). By doing so, the price function becomes:


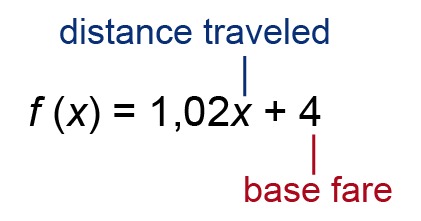
The function is a polynomial function of the first degree. It creates the following linear graph: 

Because the graph of the function is a line that does not pass through the origin, there is a linear relationship between the distance traveled and the price of the ride. This could also have been deduced directly from the equation of the function without plotting.

The degree of the function [[$ f (x) = 1,02x + 4 $]] is one. The graph of a first-order polynomial function is always a straight line. Thus, there is a linear relationship between the distance traveled and the price of a taxi ride.