2. The definition of a function
The definition of a function
A function [[$ f $]] from a set [[$ A $]] to a set [[$ B $]] is a rule that assosiates each [[$ x $]] of set [[$ A $]] to exactly one [[$ y $]] of set [[$ B $]].
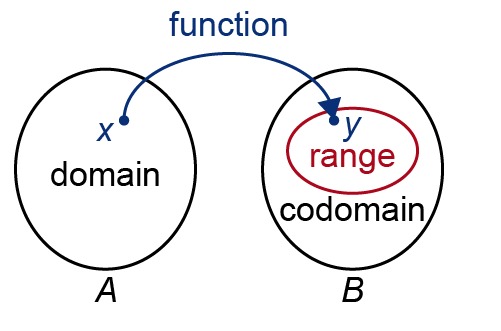 If [[$ y $]] is a function of [[$ x $]], then all the possible values of [[$ x $]] form a domain or an output set, and all the possible values of [[$ y $]] are form a codomain. The function's range or set of values is obtained from the codomain by using different values of [[$ x $]]. The range is a subset of the codomain. In mathematical examples, the domains usually consist of numbers. However, in tasks that describe real-world phenomena, the domains can be made up of anything, such as animals.
If [[$ y $]] is a function of [[$ x $]], then all the possible values of [[$ x $]] form a domain or an output set, and all the possible values of [[$ y $]] are form a codomain. The function's range or set of values is obtained from the codomain by using different values of [[$ x $]]. The range is a subset of the codomain. In mathematical examples, the domains usually consist of numbers. However, in tasks that describe real-world phenomena, the domains can be made up of anything, such as animals.
The expression of a function is often denoted by [[$ f (x) $]] instead of [[$ y $]]. Thus, the function's variable is [[$ x $]]. The values of the function are determined by using the values of [[$ x $]] according to a certain rule. Depending on the context, the function and variable can also be denoted by other letters. For example, if speed is a function of time, it is usually denoted by [[$ v (t) $]].
Example 1
What are the domain, codomain and range of the expression [[$ x \rightarrow 2x + 1 $]] ?
Solution:
The function machine works as follows: “It can only accept the numbers [[$ 0 $]], [[$ 1 $]], [[$ 2 $]], [[$ 3 $]] and [[$ 4 $]]. Any number from zero to nine can come out. ”
The domain of the description consists of all the elements (in this case numbers) that can be entered into the machine. These numbers are [[$ 0 $]], [[$ 1 $]], [[$ 2 $]], [[$ 3 $]] and [[$ 4 $]]. The codomain consists of all the possible outputs, which are the numbers [[$ 0 $]], [[$ 1 $]], [[$ 2 $]], [[$ 3 $]] and [[$ 4 $]], [[$ 5 $]], [[$ 6 $]], [[$ 7 $]], [[$ 8 $]], [[$ 9 $]]. Note that this does not necessarily mean that all these numbers also come out of the machine. The numbers that are actually obtained from the machine are [[$1$]], [[$3$]], [[$5$]], [[$7$]] and [[$9$]]. These form the function machine's range. The range always consists of codomain elements. It can contain all the elements of the codomain or, as is the case in this example, part of them.
Answer: The domain of the expression [[$ x \rightarrow 2x + 1 $]] is {[[$ 0 $]], [[$ 1 $]], [[$ 2 $]], [[$ 3 $]], [[$ 4 $]]}. The codomain of the expression is {[[$ 0 $]], [[$ 1 $]], [[$ 2 $]], [[$ 3 $]] and [[$ 4 $]], [[$ 5 $]], [[$ 6 $]], [[$ 7 $]], [[$ 8 $]], [[$ 9 $]]}. The range of the expression is {[[$ 1 $]], [[$ 3 $]], [[$ 5 $]], [[$ 7 $]], [[$ 9 $]]}.
Example 2
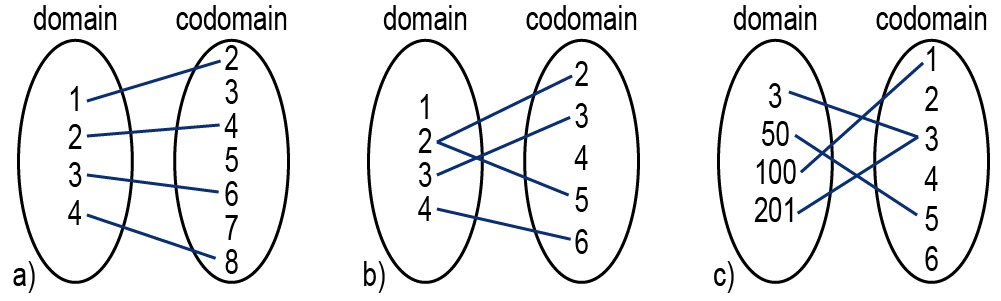
Which of the following images describe functions?
Solution:
a) This is a function, because each number in the domain corresponds to exactly one number in the codomain. The range value is obtained by multiplying the domain value by two.
b) This is not a function. The domain number [[$ 2 $]] is mapped to two different values. The function must always give a value according to the same rules. In addition, the domain value [[$ 1 $]] is not mapped to anything.
c) This is a function. The function maps domain values as numbers that are the sum of the numbers in the range of numbers.
Note! A domain element cannot be described as two different codomain elements. However, two different domain elements can be described as the same codomain element.
Example 3
The values of the function [[$ f $]] are calculated by the rule “Subtract one from the number and multiply the difference by [[$ 3 $]]”.
a) Form the expression of the function.
Let the number be denoted by the letter [[$ x $]], where [[$ f(x) = (x - 3) \cdot 3 = 3x - 3 $]].
b) Calculate the value of the function at [[$ 6 $]].
Place the number [[$ 6 $]] in place of [[$ x $]] in the previous function:
[[$ f(6) = 3 \cdot 6 - 3 = 15 $]].
Exercises
Basic exercises
Applied exercises
Challenging exercises
1/02. Submission folder for answers
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.