Tehtävät
Teksti
370
)
%2BP%5Cleft(1%5C%20oikein%5Cright)%2BP%5Cleft(2%5C%20oikein%5Cright)%2BP%5Cleft(3%5C%20oikein%5Cright)%2BP%5Cleft(4%5C%20oikein%5Cright))
%5E%7B15%7D%2B%5Cbinom%7B15%7D%7B1%7D%5Ccdot%5C%20%5Cleft(1-%5Cfrac%7B1%7D%7B2%7D%5Cright)%5E%7B15-1%7D%2B%5Cbinom%7B15%7D%7B2%7D%5Ccdot%5Cleft(%5Cfrac%7B1%7D%7B2%7D%5Cright)%5E2%5Ccdot%5Cleft(1-%5Cfrac%7B1%7D%7B2%7D%5Cright)%5E%7B15-2%7D%2B%5Cbinom%7B15%7D%7B3%7D%5Ccdot%5Cleft(%5Cfrac%7B1%7D%7B2%7D%5Cright)%5E3%5Ccdot%5Cleft(1-%5Cfrac%7B1%7D%7B2%7D%5Cright)%5E%7B15-5%7D%2B%5Cbinom%7B15%7D%7B4%7D%5Ccdot%5Cleft(%5Cfrac%7B1%7D%7B2%7D%5Cright)%5E4%5Ccdot%5Cleft(1-%5Cfrac%7B1%7D%7B2%7D%5Cright)%5E%7B15-4%7D)
 Siis todennäköisyys, että opiskelija läpäisee testin, on 1-P(korkeintaan 4 arvausta oikein)=1-0,05892...=0,9410...≈0,94.
Siis todennäköisyys, että opiskelija läpäisee testin, on 1-P(korkeintaan 4 arvausta oikein)=1-0,05892...=0,9410...≈0,94.
371
a)
383%3DP%5Cleft(ei%5C%20yht%C3%A4%C3%A4n%5Cright)%2BP%5Cleft(yksi%5Cright))
%5En%2B%5Cbinom%7Bn%7D%7B1%7D%5Ccdot0%7B%2C%7D7%5E1%5Ccdot%5Cleft(1-0%7B%2C%7D7%5Cright)%5E%7Bn-1%7D)

Läpipääsyyn vaaditaan 15 oikeaa vastausta, ja opiskelija tietää 10 vastausta, joten hän pääsee läpi arvaamalla oikein 5 vastausta lopuista 15:sta.
Koska opiskelija arvaa vastauksen 15 tehtävään, joissa vastausvaihtoehtoja on kaksi, tilannetta voidaan ajatella 15 yrityksen toistokokeena, jossa onnistumistodennäköisyys on jokaisella toistolla 1/2.
Opiskelija tarvitsee läpipääsyyn tietämiensä 10 vastauksen lisäksi vähintään 5 oikein arvattua vastausta eli 5, 6, … tai 10 oikeaa arvausta. Lasketaan vastatapahtuman "korkeintaan 4 oikeaa arvausta" eli "0, 1, 2, 3 tai 4 oikeaa arvausta" todennäköisyys. Tapahtumat ovat erilliset oikeiden vastausten eri lukumäärille, joten yhteenlaskusäännöllä saadaan
371
a)
Ajatellaan tilannetta toistokokeena, jossa onnistumisen todennäköisyys on P(O) = 0,33 ja toistoja on 12. Tapahtuman "enintään 9 O:ta" vastatapahtuma on "vähintään 10 O:ta" eli "10, 11 tai 12 O:ta". Erillisten tapahtumien yhteenlaskusäännöllä saadaan
)
%2BP%5Cleft(11%5C%20O%3Ata%5Cright)%2BP%5Cleft(12%5C%20O%3Ata%5Cright))
%5E%7B12-10%7D%2B%5Cbinom%7B12%7D%7B11%7D%5Ccdot0%7B%2C%7D33%5E%7B11%7D%5Ccdot%5Cleft(1-0%7B%2C%7D33%5Cright)%5E%7B12-11%7D%2B0%7B%2C%7D33%5E%7B12%7D)

)
)



)
%2BP%5Cleft(4%5C%20B%3At%C3%A4%5Cright))
%5E%7B12-3%7D%2B%5Cbinom%7B12%7D%7B4%7D%5Ccdot0%7B%2C%7D17%5E4%5Ccdot%5Cleft(1-0%7B%2C%7D17%5Cright)%5E%7B12-4%7D)


Siispä
b)
Nyt toistokokeen onnistumistodennäköisyys on P(B) = 0,17. Tapahtumat "joukossa on kolme B:tä" ja "joukossa on "neljä B:tä" ovat erilliset, joten yhteenlaskusäännöllä saadaan
383
Tapahtuman "ainakin kaksi itää" vastatapahtuma on "korkeintaan yksi itää" eli "ei yhtään tai yksi itää". Lasketaan vastatapahtuman todennäköisyys.
Ajatellaan tilannetta toistokokeena, jossa onnistumisen todennäköisyys on P(sipuli itää) = 0,7.
Siis
%3D1-%5Cleft(0%7B%2C%7D3%5En%2Bn%5Ccdot0%7B%2C%7D7%5Ccdot0%7B%2C%7D3%5E%7Bn-1%7D%5Cright))
Etsitään siis pienin luonnollinen luku n, jolle %5Cge0%7B%2C%7D99) eli
eli%5Cge0%7B%2C%7D99)
Etsitään luku n ratkaisemalla ensin yhtälö %3D0%7B%2C%7D99) symbolisen laskennan ohjelmalla
symbolisen laskennan ohjelmalla
Saadaan n=6,05...
Saadaan n = 6,05… Mitä enemmän sipuleita istutetaan, sitä suurempi on todennäköisyys, että vähintään haluttu määrä sipuleita itää. Sipuleita on siis istutettava vähintään 7.
Teksti
4.4 Normaalijakauma



%3DP%5Cleft(-0%7B%2C%7D86%5Cle%20Z%5Cle0%7B%2C%7D38%5Cright))
-P%5Cleft(Z%5Cle-0%7B%2C%7D86%5Cright)%3D%5CPhi%5Cleft(0%7B%2C%7D38%5Cright)-%5CPhi%5Cleft(-0%7B%2C%7D86%5Cright))
-%5Cleft(1-%5CPhi%5Cleft(0%7B%2C%7D86%5Cright)%5Cright))
-1%2B%5CPhi%5Cleft(0%7B%2C%7D86%5Cright))


Esimerkki. Mailan kestoikä noudattaa normaalijakaumaa.Kestoiän odotusarvo on 960 peliminuutttia ja keskihajonta 105 min. Millä todennäköisyydellä maila hajoaa 870 ja 1000 min välillä?
Ratkaisu
Tapa1:
X= Mailan kestoikä (min)
X~N(960,105)
P(870 ≤ X ≤1000)
Normitetaan satunaismuuttuja X.
Kun X=1000, niin
Kun X=870
Tapa 2:
Todennäköisyyslaskurilla saadaan kysytyksi todennäköisyydeksi 0,4527 eli noin 45%
481
X= betonisäkin massa (kg)
X~N(µ; 0,9)
Mikä on odotusarvo µ, kun P(X>25)= 0,95 eli P(X≤25)=0,05?
Ratkaistaan geogebran CAS-laskimella
µ≈26,48
463
a) 0,1587 ≈ 16%
b) 0,1587 ≈ 16%
c) 0,6827 ≈ 67%
466
a) 16973,8 ≈ 17000
b) 14695,9 ≈ 14700
c) 17464,4 ≈ 17500
468
a) C 0,1587
b) A 0,2266
c) B 0,1587
d) D 0,0668
469
471
475
477
483
Teksti
442
a) Funktio f ei ole tiheysfunktio, koska sen kuvaajan ja x-akselin väliin
jäävän alueen pinta-ala ei ole 1 (vaan 2).
Funktio g ei ole tiheysfunktio, koska sen kuvaajan ja x-akselin väliin
jäävän alueen pinta-ala ei ole 1 (vaan suurempi).
Funktio h ei ole tiheysfunktio, koska se saa negatiivisia arvoja.
b) Funktio k on tiheysfunktio, koska se ei saa missään negatiivisia arvoja
ja lisäksi sen kuvaajan ja x-akselin väliin jäävän alueen pinta-ala on 1.
444
a)
%3DP%5Cleft(X%5Cle%20a%5Cright)-P%5Cleft(X%3Da%5Cright))
) tarkoittaa funktion kuvaajan ja x-akselin väliin jäävä pinta-ala kohdassa x=a eli janan pinta-alaa. Janan pinta-ala on nolla eli jakautuneen satunnaismuuttujan yksittäisen arvon todennäköisyys on nolla eli
tarkoittaa funktion kuvaajan ja x-akselin väliin jäävä pinta-ala kohdassa x=a eli janan pinta-alaa. Janan pinta-ala on nolla eli jakautuneen satunnaismuuttujan yksittäisen arvon todennäköisyys on nolla eli
%3D0) . Siten
. Siten%3DP%5Cleft(X%3Ca%5Cright)%3D0%7B%2C%7D37) .
.
b)
c)Tapahtumat X > a ja X ≤ a ovat oistensa vastatapahtumia, joten
d)Tapahtumat X ≥ b ja X < b ovatvastatapahtumia, joten
445
Kuvassa A on funktion f kuvaajan ja x-akselin väliin välillä a ≤ x ≤ b
jäävän alueen pinta-ala. Kun f on satunnaismuuttujan X tiheysfunktio,
tämä pinta-ala on sama kuin todennäköisyys P(a ≤ X ≤ b), joka on sama
kuin P(a < X ≤ b). Siis kuvaan A sopivat merkinnät II ja VI.
Kuvassa B on funktion f kuvaajan ja x-akselin väliin välillä x > b jäävän
alueen pinta-ala, joka on sama kuin todennäköisyys P(X > b) eli merkintä V.
Kuvassa C on funktion f kuvaajan ja x-akselin väliin välillä x < b jäävän
alueen pinta-ala, joka on sama kuin todennäköisyys P(X ≤ b) eli merkintä I.
Kuvassa D on funktion f kuvaajan ja x-akselin väliin väleillä x < a ja x > b
jäävän kaksiosaisen alueen pinta-ala, joka on sama kuin todennäköisyys
P(X < a tai X > b). Tapahtuman "X < a tai X > b" vastatapahtuma on
tapahtuma a ≤ X ≤ b, jonka todennäköisyys näkyy kuvassa valkoisen
alueen pinta-alana. Siis kuvaan merkittyä (väritettyä) pinta-alaa vastaa
todennäköisyys P(X < a tai X > b) = 1 − P(a ≤ X ≤ b) eli merkintä III.
Kuvassa A on funktion f kuvaajan ja x-akselin väliin välillä a ≤ x ≤ b
jäävän alueen pinta-ala. Kun f on satunnaismuuttujan X tiheysfunktio,
tämä pinta-ala on sama kuin todennäköisyys P(a ≤ X ≤ b), joka on sama
kuin P(a < X ≤ b). Siis kuvaan A sopivat merkinnät II ja VI.
Kuvassa B on funktion f kuvaajan ja x-akselin väliin välillä x > b jäävän
alueen pinta-ala, joka on sama kuin todennäköisyys P(X > b) eli merkintä V.
Kuvassa C on funktion f kuvaajan ja x-akselin väliin välillä x < b jäävän
alueen pinta-ala, joka on sama kuin todennäköisyys P(X ≤ b) eli merkintä I.
Kuvassa D on funktion f kuvaajan ja x-akselin väliin väleillä x < a ja x > b
jäävän kaksiosaisen alueen pinta-ala, joka on sama kuin todennäköisyys
P(X < a tai X > b). Tapahtuman "X < a tai X > b" vastatapahtuma on
tapahtuma a ≤ X ≤ b, jonka todennäköisyys näkyy kuvassa valkoisen
alueen pinta-alana. Siis kuvaan merkittyä (väritettyä) pinta-alaa vastaa
todennäköisyys P(X < a tai X > b) = 1 − P(a ≤ X ≤ b) eli merkintä III.
Teksti
422
%3D%5Cfrac%7B3%7D%7B8%7D)
%3D%5Cfrac%7B1%7D%7B4%7D)
%3D%5Cfrac%7B1%7D%7B8%7D)
%3D%5Cfrac%7B1%7D%7B4%7D)
%3D%5Cfrac%7B3%7D%7B8%7D%5Ccdot0%2B%5Cfrac%7B1%7D%7B4%7D%5Ccdot1%2B%5Cfrac%7B1%7D%7B8%7D%5Ccdot2%2B%5Cfrac%7B1%7D%7B4%7D%5Ccdot3%3D1%7B%2C%7D25)
![D\left(X\right)=\sqrt[]{\frac{3}{8}\left(0-2{,}25\right)^2+\frac{1}{4}\left(1-2{,}25\right)^2+\frac{1}{8}\left(2-2{,}25\right)^2+\frac{1}{4}\left(4-2{,}25\right)^2}=1{,}198...\approx1{,}20](https://math-demo.abitti.fi/math.svg?latex=D%5Cleft(X%5Cright)%3D%5Csqrt%5B%5D%7B%5Cfrac%7B3%7D%7B8%7D%5Cleft(0-2%7B%2C%7D25%5Cright)%5E2%2B%5Cfrac%7B1%7D%7B4%7D%5Cleft(1-2%7B%2C%7D25%5Cright)%5E2%2B%5Cfrac%7B1%7D%7B8%7D%5Cleft(2-2%7B%2C%7D25%5Cright)%5E2%2B%5Cfrac%7B1%7D%7B4%7D%5Cleft(4-2%7B%2C%7D25%5Cright)%5E2%7D%3D1%7B%2C%7D198...%5Capprox1%7B%2C%7D20)


%3DP%5Cleft(2%5C%20klaavaa%5Cright)%3D%5Cfrac%7B1%7D%7B4%7D)
%3DP%5Cleft(1%5C%20kruuna%5Cright)%3D%5Cfrac%7B1%7D%7B2%7D)
%3DP%5Cleft(2%5C%20kruunaa%5Cright)%3D%5Cfrac%7B1%7D%7B4%7D)
%3D0%5Ccdot%5Cfrac%7B1%7D%7B4%7D%2B%5Cleft(-1%5Cright)%5Ccdot%5Cfrac%7B1%7D%7B2%7D%2B%5Ccdot2%5Ccdot%5Cfrac%7B1%7D%7B4%7D%3D0)


%3D%5Cfrac%7B50%7D%7B3%5C%20000%5C%20000%7D%5Ccdot999%2B%5Cfrac%7B100%7D%7B3%5C%20000%5C%20000%7D%5Ccdot99%2B%5Cfrac%7B30%5C%20000%7D%7B3%5C%20000%5C%20000%7D%5Ccdot19%2B%5Cfrac%7B300%5C%20000%7D%7B3%5C%20000%5C%20000%7D%5Ccdot1%2B%5Cfrac%7B420%5C%20000%7D%7B3%5C%20000%5C%20000%7D%5Ccdot0%2B%5Cfrac%7B2%5C%20249%5C%20850%7D%7B3%5C%20000%5C%20000%7D%5Ccdot-1%3D-0%7B%2C%7D44)

%5C%5C%0A%5Chline%0A2%26%5Cfrac%7B1%7D%7B24%7D%5C%5C%0A3%26%5Cfrac%7B1%7D%7B12%7D%5C%5C%0A4%26%5Cfrac%7B1%7D%7B8%7D%5C%5C%0A5%26%5Cfrac%7B1%7D%7B6%7D%5C%5C%0A6%26%5Cfrac%7B1%7D%7B6%7D%5C%5C%0A7%26%5Cfrac%7B1%7D%7B6%7D%5C%5C%0A8%26%5Cfrac%7B1%7D%7B8%7D%5C%5C%0A9%26%5Cfrac%7B1%7D%7B12%7D%5C%5C%0A10%26%5Cfrac%7B1%7D%7B24%7D%0A%5Cend%7Barray%7D)
%3D2%5Ccdot%5Cfrac%7B1%7D%7B24%7D%2B3%5Ccdot%5Cfrac%7B1%7D%7B12%7D%2B4%5Ccdot%5Cfrac%7B1%7D%7B8%7D%2B5%5Ccdot%5Cfrac%7B1%7D%7B6%7D%2B6%5Ccdot%5Cfrac%7B1%7D%7B6%7D%2B7%5Ccdot%5Cfrac%7B1%7D%7B6%7D%2B8%5Ccdot%5Cfrac%7B1%7D%7B8%7D%2B9%5Ccdot%5Cfrac%7B1%7D%7B12%7D%2B10%5Ccdot%5Cfrac%7B1%7D%7B24%7D%3D6)




 Siten
Siten


%3D1%5Ccdot0%7B%2C%7D65%2B1%5Ccdot0%7B%2C%7D75%2B1%5Ccdot0%7B%2C%7D54%3D1%7B%2C%7D94)


%5C%5C%0A%5Chline%0A5%260%7B%2C%7D361%5C%5C%0A1%260%7B%2C%7D185%5C%5C%0A-5%260%7B%2C%7D111%0A%5Cend%7Barray%7D) e
e
%3DP%5Cleft(punainen%5C%20JA%5C%20punainen%5C%20TAI%5C%20vihre%C3%A4%5C%20JA%5C%20vihre%C3%A4%5Cright))

%3DP%5Cleft(punainen%5C%20JA%5C%20Vihre%C3%A4%5Cright)%3D%5Cfrac%7B5%7D%7B9%7D%5Ccdot%5Cfrac%7B1%7D%7B3%7D%3D0%7B%2C%7D1851...%5Capprox0%7B%2C%7D185)
%3D%5Cfrac%7B1%7D%7B9%7D%3D0%7B%2C%7D1111...%5Capprox0%7B%2C%7D111)
%3D5%5Ccdot0%7B%2C%7D361%2B1%5Ccdot0%7B%2C%7D185%2B-5%5Ccdot0%7B%2C%7D111%3D1%7B%2C%7D435)
a)
b)
423
a)
b)
424
a)
b)
Koska on 2 249 850 kpl arpaa jolla ei saa penniäkään, joten jos osetetaan 2 249 851 arpaa, ainakin yhdellä arvalla saa jonkin voiton.
425
a)
b)
427
a)
b)
428
5 punaista
3 vihreää
1 musta
429
430
433
435
Teksti
Kertymäfunktio
Satunnaismuuttujan X kertymäfunktio on
Kertymäfunktio arvo kohdassa x on kohdan x jasit pienempien satunnaismuuttujan arvojen todennäköisyyksien summa
414
a)
b)
c)
401
a) Pistetodennäköisyyksien summa on yksi, joten
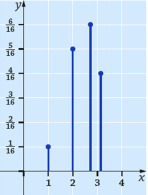
406
a)
b)
409
412
415
Teksti
351
%3DP%5Cleft(%5Cmathrm%7B2%5C%20ruskeaa%5C%20TAI%5C%202%5C%20mustaa%5C%20TAI%5C%202%5C%20%5Csin%20ist%C3%A4%7D%5Cright))
%2BP%5Cleft(2%5C%20mustaa%5Cright)%2BP%5Cleft(2%5C%20%5Csin%20ist%C3%A4%5Cright)%7D)




 eri tavalla
eri tavalla
 eri tavalla ja
eri tavalla ja
 eri tavalla.
eri tavalla.
%3D%5Cfrac%7B44%7D%7B120%7D%3D%5Cfrac%7B11%7D%7B30%7D)
%3DP%5Cleft(%5Csim%5Cright))
Puheenjohtajaa voidaan valita
 eri tavalla
eri tavalla
 eri tavalla
eri tavalla
%3D13%5Ccdot12%5Ccdot11%3D1716)

c)

 Koska yksi on ainakin päällä, tästä vähenettävä yhden ''suljettu'' vaihto.
Koska yksi on ainakin päällä, tästä vähenettävä yhden ''suljettu'' vaihto.

 , eli lähes 1,6 miljoonaa
Lotossa valitaan 7 oikeita numeroa 40 vaihtoehtosta
, eli lähes 1,6 miljoonaa
Lotossa valitaan 7 oikeita numeroa 40 vaihtoehtosta
 , eli lähes 19 miljoonaa
, eli lähes 19 miljoonaa

Jos halutaan saada 1 oikean, valitaan 3 oikeasta 1 JA 7 väärästä 2, eli



2 Ruskeaa, 6 mustaa ja 8 sisnistä
Kuoria on yhteensä 16 kpl
Tapa 1:
Tapa 2:
16 kuoren joukosta voidaan valita 2 kuorta
Kaksi ruskeaa kuorta voidaan valita yhdellä tavalla
Kaksi mustaa kurota voidaan valita
kaksi sinistä kuorta voidaan valita
Yhteensä samanväriset kuoret voidaan valita 1+15+28=44 eri tavalla
342
a)
Puheenjohtajaa voidaan valita
Sihteeriä voidaan valita
Taloudenhoitajaa voidaan valita
 eri tavalla
eri tavalla
b)
c)
344
Tapoja on yhteensä
345
Vakioveikkauksessa valitaan 13 tulosta 3 vaihtoehtosta, valinantapoja on tuloperiaatteen mukaan
Joten vakioveikkauksessa päävoitto on todennäköisempi.
346
Lasten lotossa voidaan valita 3 numeroa  tavalla.
tavalla.
Jos halutaan saada 0 oikeata, valitaan 7 väärästä numerosta 3, eli
Jos halutaan saada 1 oikean, valitaan 3 oikeasta 1 JA 7 väärästä 2, eli
Jos halutaan saada 2 oikeata, valitaan 3 oikeasta 2 JA 7 väärästä 1, eli
Jos halutaa saada kaikki oikein(3 oikein), valitaan 3 oikesta 3
347
349
452
353
355
356
Teksti
334
 eri tavalla
eri tavalla
%3D1-P%5Cleft(ei%5C%20yht%C3%A4%C3%A4n%5C%20omenaa%5Cright)%3D1-%5Cfrac%7B%5Cbinom%7B9%7D%7B2%7D%7D%7B66%7D%3D1-%5Cfrac%7B36%7D%7B66%7D%3D%5Cfrac%7B5%7D%7B11%7D%5Capprox0%7B%2C%7D45)
%3DP%5Cleft(2%5C%20omenaa%5C%20tai%5C%202%5C%20p%C3%A4%C3%A4ryn%C3%A4%C3%A4%5C%20tai%5C%202%5C%20mandariinia%5Cright))
%7D%7B66%7D%3D%5Cfrac%7B19%7D%7B66%7D%5Capprox0%7B%2C%7D29)
!%7D%3D210)



%3D10%5Ccdot16%3D160) b)
b)
%3D%5Cbinom%7B26%7D%7B2%7D%3D325)


%3D%5Cfrac%7B324632%7D%7B1533939%7D%3D0%7B%2C%7D211...%5Capprox0%7B%2C%7D21)
%3D%5Cfrac%7B%5Cbinom%7B7%7D%7B6%7D%5Ccdot%5Cbinom%7B1%7D%7B1%7D%7D%7B%5Cbinom%7B40%7D%7B7%7D%7D%3D%5Cfrac%7B7%7D%7B18643560%7D)
%3D%5Cfrac%7B%5Cbinom%7B7%7D%7B6%7D%5Ccdot%5Cbinom%7B40-7-1%7D%7B1%7D%7D%7B%5Cbinom%7B40%7D%7B7%7D%7D%3D%5Cfrac%7B28%7D%7B2330445%7D)
%3D%5Cfrac%7B%5Cbinom%7B7%7D%7B4%7D%5Ccdot%5Cbinom%7B40-7-1%7D%7B3%7D%7D%7B%5Cbinom%7B40%7D%7B7%7D%7D%3D%5Cfrac%7B4340%7D%7B466089%7D)
%3D%5Cbinom%7B5%7D%7B2%7D%5Ccdot%5Cbinom%7B7%7D%7B1%7D%3D70)
%3D%5Cbinom%7B7%7D%7B2%7D%5Ccdot%5Cbinom%7B5%7D%7B1%7D%3D105)
 V: Delegaatioita voidaan mudosta 175 eri tavalla.
V: Delegaatioita voidaan mudosta 175 eri tavalla.
!%7D%3D%5Cfrac%7B20!%7D%7B4!%5Ccdot16!%7D%3D%5Cfrac%7B20%5Ccdot19%5Ccdot18%5Ccdot17%7D%7B4%5Ccdot3%5Ccdot2%5Ccdot1%7D%3D%5Cfrac%7B5%5Ccdot19%5Ccdot3%5Ccdot17%7D%7B1%7D%3D19%5Ccdot17%5Ccdot15)
!%7D%3D%5Cfrac%7B20!%7D%7B12!%5Ccdot8!%7D%3D%5Cfrac%7B20%5Ccdot19%5Ccdot18%5Ccdot17%5Ccdot16%5Ccdot15%5Ccdot14%5Ccdot13%7D%7B8%5Ccdot7%5Ccdot6%5Ccdot5%5Ccdot4%5Ccdot3%5Ccdot2%5Ccdot1%7D%3D%5Cfrac%7B19%5Ccdot17%5Ccdot15%5Ccdot14%5Ccdot13%7D%7B7%7D)
!%7D%3D)
3 omenaa, 4 päärynää, 5 mandariinia
Hedemiä on yhteensä 12 kappaletta
12 hedelmän joukosta voidaan valita 2 hedelmää
a)
b)
321
a)
b)
322
32 korttia
1. 5 korttia
2. 5 korttia
325
10 poikaa
16 tyttöä
a)
Opiskelijoita on yhteensä 10+16=26 henkilöä
326
47 eläintä
Vilina tunnistaa 35 eläintä
Ei tuunista 12 eläintä
327
1-40
a)
b)
c)
329
5 1.opiskeljiaa
7 2.opiskelijaa
Koska delegaatioita voidaan muodosta vain kahdella tavalla:
2 1.opiskelijaa + 1 2.opiskelija
tai
2 2.opiskelijaa + 1 1.opiskelija
ja
332
333
337
338
Teksti
302
3 housua
2 pitkähihaista paitaa
1 musta t-paita
1 vaaleapunainen t-paita
2 valkoista t-paitaa
a)
b)
303
a) Nlejästä henkilöstä valitaan juoksijat 4-osuuksiseen viestiin,
Erilaisia juoksujärjestyksiä eli permutaatioita on
b) 7 henkilöstä valitaan juoksijat 5-osuuksiseen viestiin.
Erilaisia juoksujärjestyksiä on
7-alkioisen joukon 5-permutaatiota on
304
a)
b)
306
a)
b)
309
5 tyttöä
4 poikaa
a)
Aloittaja on tyttö=joka toinen on poika
Aloittajat on poika=joka toinen on tyttö
b)
Lapsia on yhteensä 9, joten niitä 9-alkioisen joukon 5-permutaatiota on
Koska jonoja on mahdollista muodosta 1200 kpl, sen todennäköisyys saadaan
310
Oikean pääsykoodin vaihtoehtoja on
Milla aikoo kokeilla eri numerosarjoja, joten hän valitsee kokeiltaviksi kolme eri numerosarjaa. Todennäköisyys, että oikea numerosarja on jokin näistä kolmesta, on
311
313
314
Teksti
265
Karjalanpiirkoita 12
Pikkupullia 9
7 molempia
5 ei kumpikaan
a)
12+2+5=19
b)
266
Asukkaita 20% on kauniita, 15% rohkeita ja 5% kauniita ja rohkeita.
a)
b)
d)
267
P(A)=Uudempi toimii todennäikösyydellä 0,95
P(B)=Vanhempi toimii todennäköisyydellä 0,75
a)
b)
c)
268
S=sinililja itää P(S)=90%=0,9
T=tulppaani itää, P(T)=95%=0,95
a)
a)
b)
d)
269
270
271
272
273
275
278
283
Teksti
243
a)
b)
245
a)
b)
c) A= Ainakin yhden punaisen valon
d)
A= Ainakin yhden vihreän valon

%3D1-P%5Cleft(%5Coverline%7BA%7D%5Cright)%3D1-0%7B%2C%7D168%3D0%7B%2C%7D832)
246
a)
b)
248
250
251
253
258
261
Teksti
223


 Todennäköisyys on laskennut
Todennäköisyys on laskennut




%3D%5Cfrac%7B14%7D%7B20%7D%3D%5Cfrac%7B7%7D%7B10%7D)
dx%3D6) (Laskin)
(Laskin)

%3D%5Cfrac%7B6%7D%7B15%7D%3D%5Cfrac%7B2%7D%7B5%7D)
%7D%7B360%7D%3D%5Cfrac%7B1%7D%7B4%7D)
%3D%5Cfrac%7BA_%7B10%7D%7D%7BA_%7Bkok%7D%7D%3D%5Cfrac%7B%5Cpi%5Ccdot17%7B%2C%7D5%5E2%7D%7B%5Cpi%5Ccdot170%7B%2C%7D5%5E2%7D%3D0%7B%2C%7D0105...%5Capprox0%7B%2C%7D01) b)
b)
) , joten
, joten )
%3D%5Cfrac%7B%5Cpi%5Ccdot%5Cleft(4%5Ccdot17%2B17%7B%2C%7D5%5Cright)%5E2%7D%7B%5Cpi%5Ccdot170%7B%2C%7D5%5E2%7D%3D0%7B%2C%7D251...%5Capprox0%7B%2C%7D25)

%3D%5Cfrac%7B%5Cpi%5Ccdot170%7B%2C%7D5%5E2-%5Cpi%5Ccdot%5Cleft(7%5Ccdot17%2B17%7B%2C%7D5%5Cright)%5E2%7D%7B%5Cpi%5Ccdot170%7B%2C%7D5%5E2%7D%5Capprox0%7B%2C%7D36)
%3D0%7B%2C%7D75-0%7B%2C%7D36%3D0%7B%2C%7D39)
%3D%5Cfrac%7B5%7D%7B65%7D%3D%5Cfrac%7B1%7D%7B13%7D%3D0%7B%2C%7D0769...%5Capprox0%7B%2C%7D08)
%3D%5Cfrac%7B60-15%2B5%7D%7B65%7D%3D%5Cfrac%7B50%7D%7B65%7D%3D%5Cfrac%7B10%7D%7B13%7D%3D0%7B%2C%7D7692...%5Capprox0%7B%2C%7D77) c)
c)
%3D%5Cfrac%7B60-50%7D%7B65%7D%3D%5Cfrac%7B10%7D%7B65%7D%3D%5Cfrac%7B2%7D%7B13%7D%3D0%7B%2C%7D1538...%5Capprox0%7B%2C%7D15)
237
1800:
1900:
2000:
224
a)
b)
225
227
228
a)
a)
Luvut, jotka ovat suurmpi kuin 5 on 6, 7, 8, 9, 10
c)
229
a)

b)

c)
b)
c)
230
a) Epätosi. Tilaston perusteella kyseisen ampumahiihtäjä osuu tauluun paljon väitettyä todennäköisemmin.
b) Tosi, koska ampumahiihtäjän todennäköisyys osua on 
c) Tosi, koska 1-0,9=0,1
d) Epätosi. Tilaston perusteella ei voida sanoa mitään varma yksittäisen laukauksen onnistumisesta.
231
a)
Koko tapahtuma kestää 65 minuuttia, ja itse purkkaus 5 minuttia, joten
b)
233
a)
koska yhden pisteen pinta-ala on 0, kysytty todennäköisyys on 0
b)
237
Teksti
201




 = Arpakuution heitossa silmä luku on enintään 3
= Arpakuution heitossa silmä luku on enintään 3
 = Luokasta on ainakin yksi poika
= Luokasta on ainakin yksi poika
 = Vähintään yhdellä koulun oppilaalla matematiikan arvosna on 10
c)
= Vähintään yhdellä koulun oppilaalla matematiikan arvosna on 10
c)
%3D%5Cfrac%7B3%7D%7B5%2B3%2B4%7D%3D%5Cfrac%7B1%7D%7B4%7D)
%3D%5Cfrac%7B3%7D%7B4%7D)
%3DP%5Cleft(%5Cmathrm%7Bon%5C%20%5Csin%20inen%7D%5Cright)%3D%5Cfrac%7B5%7D%7B12%7D)
%3D%5Cfrac%7B5%7D%7B12%7D%2B%5Cfrac%7B3%7D%7B12%7D%3D%5Cfrac%7B8%7D%7B12%7D%3D%5Cfrac%7B2%7D%7B3%7D)
209


%3D%5Cfrac%7B15%7D%7B36%7D%3D%5Cfrac%7B5%7D%7B12%7D)




212



214



%2Bab%3D0)

a) 2/3
b) 1/3
c) 1/3
202
a) 1/4
b) 3/4
c) 1/2
d) 3/13
204
a) P(A)=5/18
b) P(A)=11/36
c)P(A)=25/36
d) P(A)= 5/36
205
a)
IV; 0,4
206
a) P(A)= 2/15
b) P(A)= 4/15
c) P(A)=0
d) P(A)=8/15
e) P(A)=7/15
f) P(A)=15/15
208
5 sinistä, 3 punaista, 4 vihreätä
5 sinistä, 3 punaista, 4 vihreätä
a)
b)
c)
d)
209
4 ja 5, 3 ja 6
4 ja 6, 5 ja 5
Koska todennäköisyys saada silmäluparista summaksi 9 on  , ja summaksi 10 on
, ja summaksi 10 on  .
. , joten on aina todennäköisempi saada summaksi 9 kuin
, joten on aina todennäköisempi saada summaksi 9 kuin
210
a)
Tämän perusteella:
b)
c)
212
a)
b)
c)
214
a)
b)
c)
216
Vektorit ovat toisiaan vastaan kohtisuorassa täsmälleen silloin, kun pistetulo on 0, eli kun
Koska%3D-6) , joten ab on oltava 6
, joten ab on oltava 6
Siis%3D%5Cfrac%7B4%7D%7B36%7D%3D%5Cfrac%7B1%7D%7B9%7D)
Teksti
122








%7D%3D172%7B%2C%7D8333...%5Capprox172%7B%2C%7D83)
![s=\sqrt[]{\frac{6\cdot\left(159{,}5-172{,}83\right)^2+15\cdot\left(169{,}5-172{,}83\right)^2+12\cdot\left(179{,}5-172{,}83\right)^2+3\cdot\left(189{,}5-172{,}83\right)^2}{\left(6+15+12+3\right)}}](https://math-demo.abitti.fi/math.svg?latex=s%3D%5Csqrt%5B%5D%7B%5Cfrac%7B6%5Ccdot%5Cleft(159%7B%2C%7D5-172%7B%2C%7D83%5Cright)%5E2%2B15%5Ccdot%5Cleft(169%7B%2C%7D5-172%7B%2C%7D83%5Cright)%5E2%2B12%5Ccdot%5Cleft(179%7B%2C%7D5-172%7B%2C%7D83%5Cright)%5E2%2B3%5Ccdot%5Cleft(189%7B%2C%7D5-172%7B%2C%7D83%5Cright)%5E2%7D%7B%5Cleft(6%2B15%2B12%2B3%5Cright)%7D%7D)

153

![s=\sqrt[]{\frac{\left(548-548\right)^2+\left(547-548\right)^2+\left(547-548\right)^2+\left(548-548\right)^2+\left(549-548\right)^2+\left(549-548\right)^2}{6}}](https://math-demo.abitti.fi/math.svg?latex=s%3D%5Csqrt%5B%5D%7B%5Cfrac%7B%5Cleft(548-548%5Cright)%5E2%2B%5Cleft(547-548%5Cright)%5E2%2B%5Cleft(547-548%5Cright)%5E2%2B%5Cleft(548-548%5Cright)%5E2%2B%5Cleft(549-548%5Cright)%5E2%2B%5Cleft(549-548%5Cright)%5E2%7D%7B6%7D%7D)

A III
B II
C I
125
a) 37,5
b) 50
c) 80%
d) 40%
e) 30%
127
128
129
130
132
135
138
140
141
142
a) [1,6]
b) 3
c) ≈1,51
145
b)
Koska 1,1>0,64m, urheilija menestyy paremmin pituushypyssä.
146
148
A
B
0,23>-0,16
A poikkee enemmän kuin B
150
1,48>1,28
Opiskelija menestyy paremmin ruotsissa.
152
Välien todellisetarvot
153
Keksiarvo:
Otoskeskihajonta: