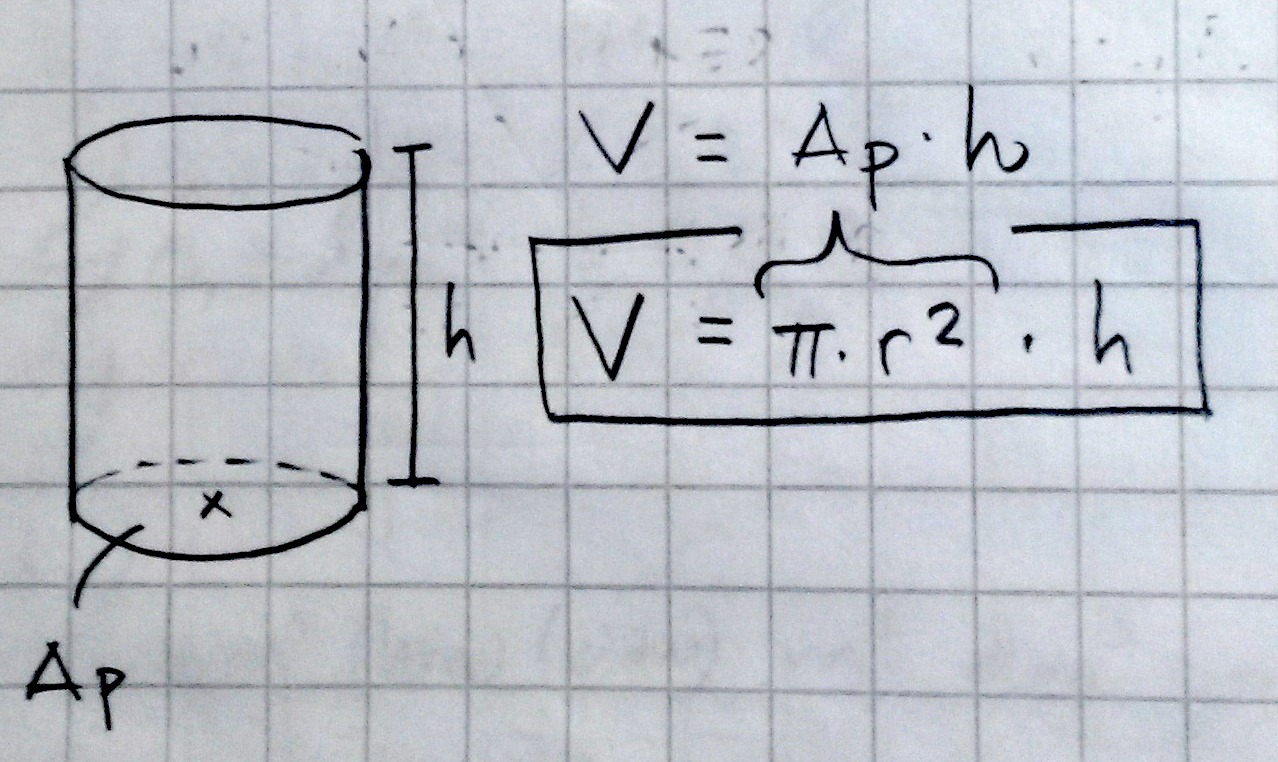Lieriö
Lieriö
Tilavuus
- Animaatio aiheesta
- Flashia ei tueta missään selaimessa enää vuoden 2020 jälkeen. Tiedoston katsomiseen tarvitsee erillisen Flash Playerin.
- Flashia ei tueta missään selaimessa enää vuoden 2020 jälkeen. Tiedoston katsomiseen tarvitsee erillisen Flash Playerin.
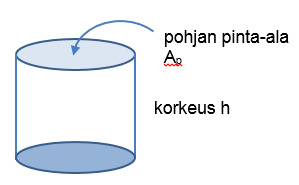
- Minkä tahansa lieriön tilavuus saadaan laskettua kertomalla pohjan pinta-ala korkeudella, eli[[$$ V=A_p \cdot h $$]]
- Ongelmaksi jää pohjan pinta-alan laskeminen, jos sitä ei tiedetä valmiiksi
- Suorakulmainen särmiö:
- pohjan pinta-ala lasketaan kertomalla kaksi mittaa keskenään (kuten minkä tahansa suorakulmion pinta-ala)
- Korkeus on sitten se jäljelle jäävä kolmas mitta eli[[$$ V=A_p \cdot h \\ V= a \cdot \ b \cdot c $$]]
- Esimerkit kirjan s.171-2
Pinta-ala
- Kolmiulotteisen kappaleen pinta-ala on kaikkien sen pintojen yhteenlaskettu pinta-ala
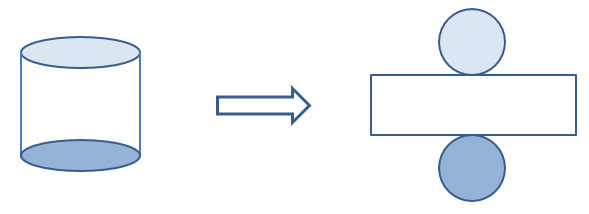
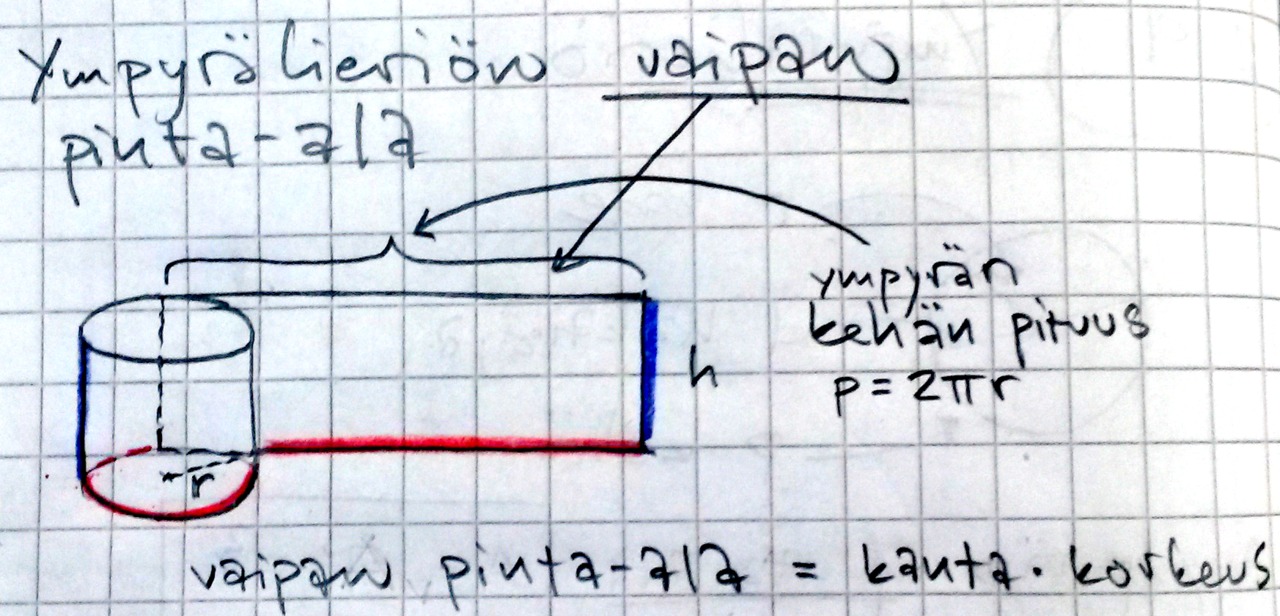
- Lieriöllä on kaksi pohjaa ja vaippa, eli [[$$ A = 2 \cdot A_p + A_v $$]]
- Ongelmaksi muodostuu taas yksittäisten sivujen pinta-alojen laskeminen
- Tässä kannattaa olla tarkkana! Piirrä mallikuva jos sitä ei ole valmiina!
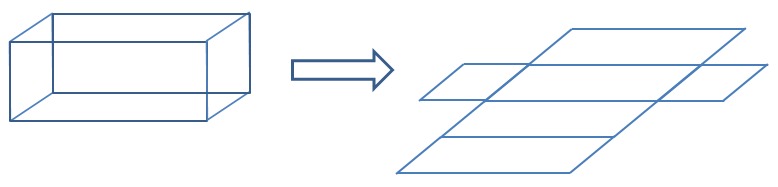
- Suorakulmainen särmiö:
- Vastakkaisia sivuja on aina 2 kpl eli [[$$ A = 2 \cdot a \cdot b + 2 \cdot a \cdot c + 2 \cdot b \cdot c $$]]
- Esimerkit kirjan s.172-3
Liitteet:
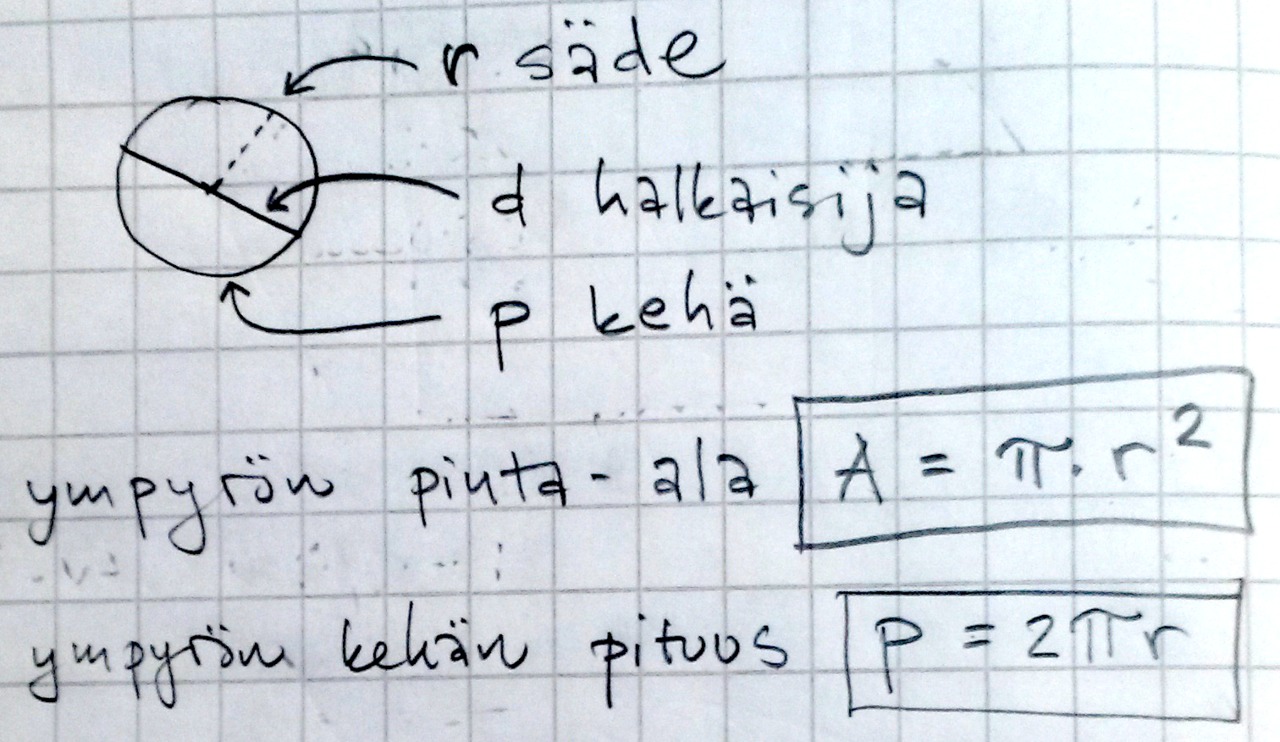
Ympyrä
Ympyrälieriö
Tutkimustehtävä
Ottakaa kaksi a4-kokoista paperia ja taitelkaa ne ympyrälieriöksi
- toinen pitkän sivun suuntaisesti
- ja toinen lyhyen
- Kumman lieriön tilavuus on suurempi?
- Kumman lieriön vaipan pinta-ala on suurempi?
- Kumman lieriön kokonaispinta-ala on suurempi jos oletetaan, että lieriöllä on molemmat pohjat?
- Perustelut laskemalla
- Jokainen tekee tarvittavat muistiinpanot omaan vihkoon