2.1 Sinifunktio ja kosinifunktio
TEHTÄVIÄ
202
a)
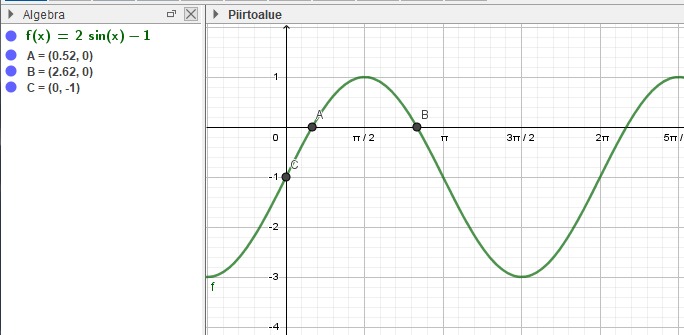
%3D2%5Csin%20x-1)
%3D2%5Csin3%5Cpi-1)


%3D-1)
)
-1)
%3D-3)
)
-1)
%3D-2) b)
b)
)
%3D0)
%3D2%5Csin0-1)
%3D-1)
%3D0%3D2%5Csin%20x-1)


yksi nollakohta on

täydellinen ratkaisu

 varmistetaan tulokset kuvasta
varmistetaan tulokset kuvasta
209
a)
%3D2%5Ccos%20x-1)
%3Df%5Cleft(%5Cfrac%7B7%5Cpi%7D%7B6%7D%5Cright))

-1)

b)
%3D0)


yksi ratkaisu


%3D-1)



yksi ratkaisu



a)
yksi nollakohta on
täydellinen ratkaisu
nollakohdat
tai

209
a)
b)
yksi ratkaisu
täydellinen ratkaisu
tai

kun 
c)
 [-3,1]
[-3,1]
d)c)
yksi ratkaisu
täydellinen ratkaisu
tai
kun 
210
a)
%3D2%2B3%5Ccos%20x)
%3D-1%2B2%5Csin%20x)



 [-3,1]
[-3,1]
kuva

b)
f(x)=3 on olemassa, sillä se kuuluu funktion arvojoukkoon
g(x)=3 ei ole olemassa, sillä se ei kuulu arvojoukkoon
213
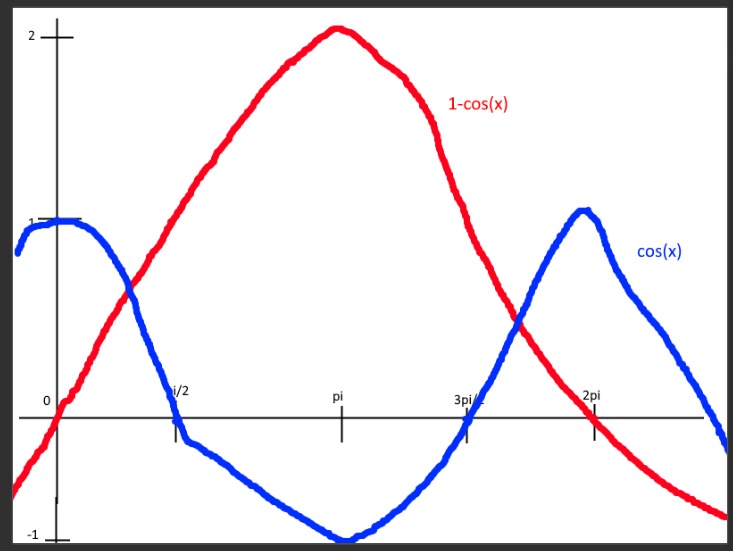
molempien käyrien jakso on 2π




%3D%5Ccos%5Cfrac%7B%5Cpi%7D%7B3%7D%3D%5Cfrac%7B1%7D%7B2%7D)



%7B%2C%7D%5C%20%5Cleft(%5Cfrac%7B11%5Cpi%7D%7B3%7D%7B%2C%7D%5C%20%5Cfrac%7B1%7D%7B2%7D%5Cright)%7B%2C%7D%5C%20%5Cleft(%5Cfrac%7B13%5Cpi%7D%7B3%7D%7B%2C%7D%5C%20%5Cfrac%7B1%7D%7B2%7D%5Cright))
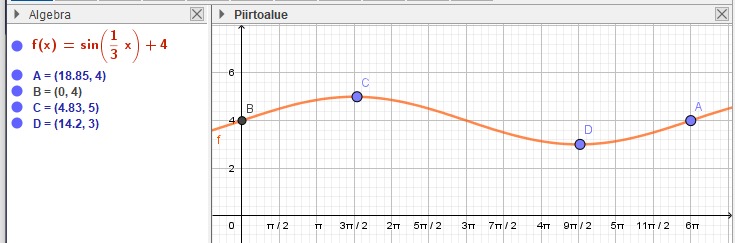
216
a) arvojoukko [-1,5;1,5], kerroin A=1,5
b) funktion f perusjakso 4π, kerroin C=0,5
c)
210
a)
[-1,5]
kuva

b)
f(x)=3 on olemassa, sillä se kuuluu funktion arvojoukkoon
g(x)=3 ei ole olemassa, sillä se ei kuulu arvojoukkoon
213

molempien käyrien jakso on 2π
yksi ratkaisu
funktion arvo kohdassa
kaikki ratkaisut
tai
ratkaisut välillä ![\left[2\pi{,}\ 4\pi\right]](https://math-demo.abitti.fi/math.svg?latex=%5Cleft%5B2%5Cpi%7B%2C%7D%5C%204%5Cpi%5Cright%5D)
leikkauspisteet
216
a) arvojoukko [-1,5;1,5], kerroin A=1,5
b) funktion f perusjakso 4π, kerroin C=0,5
c)
