Sivujen pituuksien laskeminen
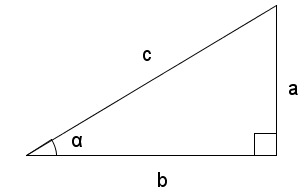
Pythagoraan lauseella voidaan laskea suorakulmaisen kolmion tuntemattoman sivun pituus, kun kaksi muuta sivua tunnetaan.
[[$$ a^2 + b^2 = c^2 $$]]
Hypotenuusan pituuden laskeminen
[[$$ a^2 + b^2 = c^2\\ c^2 = a^2 + b^2 \text{ || } \sqrt{ }\\ c = \sqrt{a^2+b^2} $$]]Esim. Suorakulmaisen kolmion kaksi lyhyempää sivua ovat 4,3 ja 5,7 cm. Laske pisimmän sivun (hypotenuusa) pituus.
[[$$ 4,3^2 + 5,7^2 = c^2\\ c^2 = 4,3^2 + 5,7^2 \text{ || } \sqrt{ }\\ c = \sqrt{4,3^2+5,7^2}\\ c = \sqrt{50,98}\\ c=7,140... \approx 7,14 cm $$]]
Kateetin pituuden laskeminen
[[$$ a^2 + b^2 = c^2 \text{ || } -b^2 \\a^2 = c^2 - b^2 \text{ || } \sqrt{ }\\a=\sqrt{c^2 - b^2} $$]]Esim. Suorakulmaisen kolmion kaksi pidempää sivua ovat 12,6 cm ja 9,4 cm. Laske lyhimmän sivun pituus.[[$$ a^2 + 9,4^2 = 12,6^2 \text{ || } -9,4^2 \\a^2 = 12,6^2 - 9,4^2 \text{ || } \sqrt{ }\\ a=\sqrt{12,6^2 - 9,4^2}\\ a=\sqrt{70,4}\\ a=8,390... \approx 8,4 cm $$]]