3.6 Gravitaatio
Yleinen gravitaatiolaki
Kappaleen painon määritlemä, [[$G=mg$]] on johdannainen yleisestä gravitaatiolaista. Yleinen gravitaatiolaki kuvaa erittäin tarkasti useimpien taivaankappaleiden liikettä. Sen perusteella on voitu ennustaa taivaankappaleiden liikkeitä pitkille aikaväleille sekä suunnitella avaruuslentojen ja satelliittien ratoja.
Yleinen gravitaatiolaki
[[$ \quad G=\gamma\dfrac{m_1m_2}{r^2}, $]]
missä [[$ \gamma $]] on gravitaatiovakio, suuruudeltaan [[$\text{6,674}\cdot 10^{-11}\dfrac{\text{Nm}^2}{\text{kg}^2} $]], [[$m_1$]] ja [[$m_2$]] ovat kappaleiden massat, joiden välillä gravitaatiovuorovaikutus esiintyy ja [[$r$]] on kappaleiden välinen etäisyys.
Gravitaation alainen liike
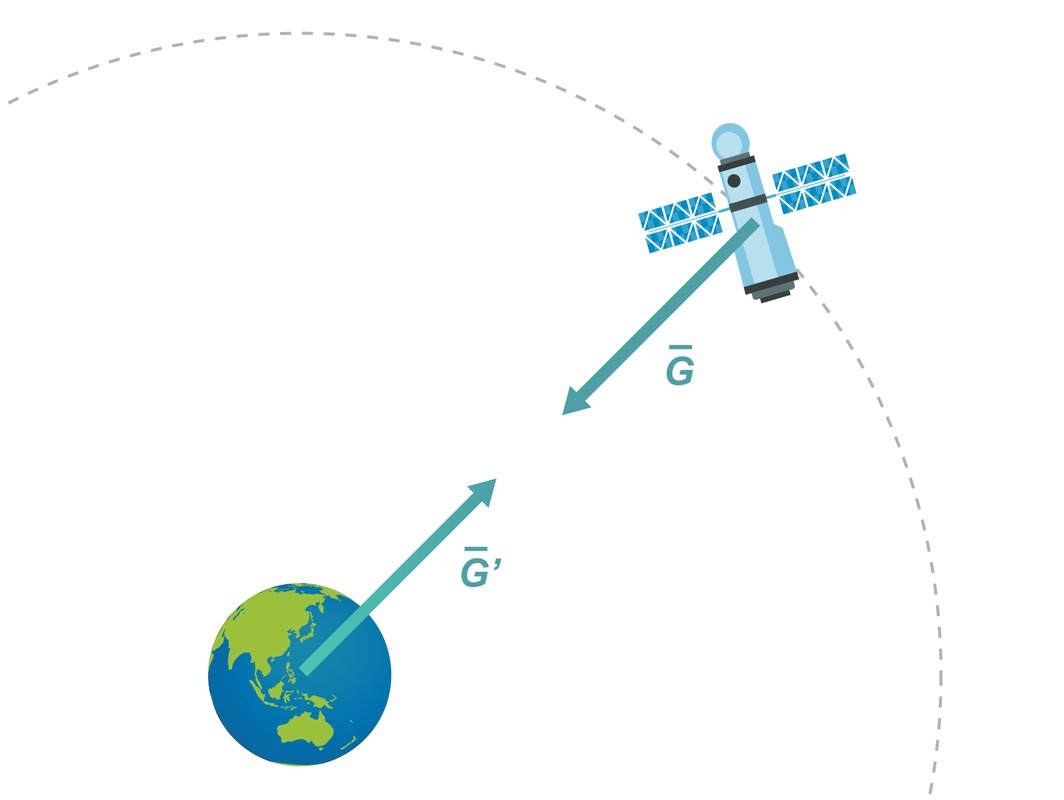Gravitaatiovuorovaikutuksessa vuorovaikuttaviin kappaleisiin kohdistuu voiman ja vastavoiman lain mukaan yhtä suuri mutta vastakkaissuuntainen voima. Maata kiertävään satelliittiin ja Maahan vaikuttaa siis yhtä suuri voima. Koska kappaleiden massat ovat erisuuret, voimat muuttavat kappaleiden liikkeitä eri tavoin dynamiikan peruslain mukaisesti.
[[$\quad a=\dfrac{F}{m}$]]
Yleinen gravitaatiolaki sopii taivaankappaleiden liikkeen mallintamiseen, jos vuorovaikuttavien kappaleiden välinen voima pysyy vakiona. Tällainen tilanne esiintyy, kun kappaleiden välinen etäisyys ei muutu. Tällöin rata on ympyrä, ja liikutaan tasaisessa ympyräliikkeessä. Satelliittien ja Kuun liikettä Maan ympäri sekä planeettojen liikettä Auringon ympäri voidaan monissa tilanteissa mallintaa ympyräratoina, vaikka todellisuudessa radat ovat lievästi elliptisiä.
Avaruudessa ollaan ilmakehän yläpuolella, eikä ilmanvastus vaikuta liikkeeseen. Avaruudessa liikkuvaan satelliittiin tai taivaankappaleeseen ei kohdistu gravitaatiovoiman lisäksi muita voimia. Gravitaatio pitää kappaleen ympyräradalla ja saa aikaan ympyrärataehdon mukaisen normaalikiihtyvyyden.
Gravitaatiokenttä
Gravitaation aiheuttaja on massa. Gravitaatiolain mukaan vuorovaikutus on kahden massapisteen välinen ja voiman suuruus ilmaisee tämän vuorovaikutuksen voimakkuutta. Jotta gravitaatio voidaan tarkastella vain yhden kappaleen näkökulmasta ja vertailla massallisten kappaleiden kykyä synnyttää gravitaatiovuorovaikutusta, edellytetään käsitettä gravitaatiokenttä. Massallinen kappale luo ympärilleen gravitaatiokentän. Tähän kenttään tuotuun toiseen massalliseen kappaleeseen vaikuttaa gravitaatiovoima. Massa A on vuorovaikutuksessa massan B luoman kentän kanssa ja päinvastoin. Gravitaatiokenttä on vektorisuure, eli sillä on suuruus ja suunta.
Gravitaatiokentän voimakkuus on gravitaatiovoiman ja massan suhde. Jakamalla voima massalla saadaan kenttään tuodun kappaleen massasta riippumaton, kentän voimakkuutta kuvaava suure.
Gravitaatiokentän voimakkuus
[[$ g=\dfrac{G}{m},$]] missä [[$ G $]] on kappaleeseen kohdistuva gravitaatiovoima ja [[$m$]] kappaleen massa. Sijoittamalla tähän Newtonin gravitaatiolain mukainen voima lauseke tulee muotoon
[[$ \quad g=\gamma\dfrac{M}{r^2}$]].
Tässä [[$M$]] on kentän aiheuttavan kappaleen massa ja [[$r$]] on etäisyys tämän massakeskipisteestä.
Gravitaatiokentän voimakkuus on sama kuin kappaleen putoamiskiihtyvyys gravitaatiokentässä.
Gravitaatio ja energia
Kun kappaletta siirretään kohti tai poispäin massapisteestä, se liikkuu gravitaatiovoiman suuntaisesti. Tällöin kappaleen potentiaalienergia muuttuu.
| Potentiaalienergia kasvaa, kappaleseen tehdään työtä | Kappale siirtyy gravitaatiokentän suuntaa vastaaan, esim. poispäin maapallosta |
| Potentiaalienergia pienenee, gravitaatiokenttä tekee työtä | Kappale siirtyy gravitaatiokentän suuntaan, esim. kohti maapalloa |
| Potentiaalienergia ei muutu, kappaleeseen ei tehdä työtä | Kappaleen etäisyys gravitaatikentän aiheuttajasta ei muutu, esim. kappale kiertää maapalloa ympyräradalla |
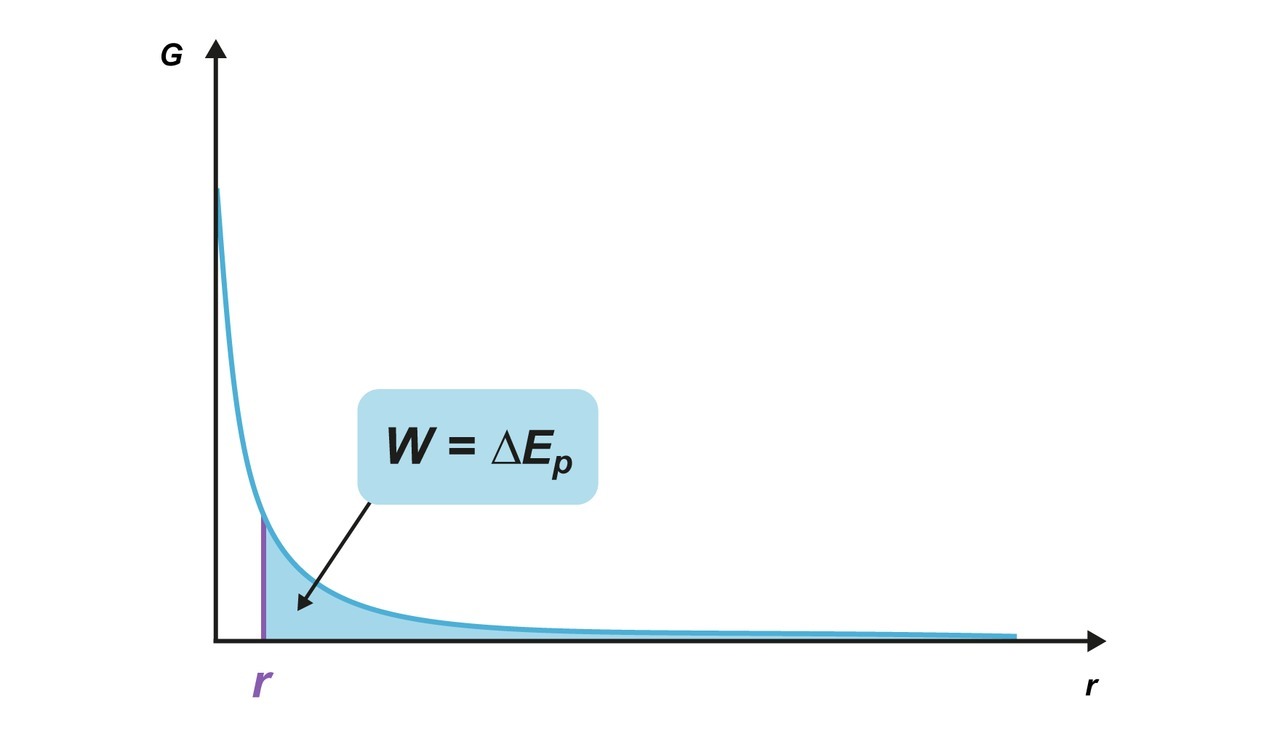
Lähellä maanpintaa gravitaatiokenttä ja gravitaatiovoima pysyvät likimain vakiona, ja tehty työ lasketaan gravitaatiovoiman ja siirtymän tulona: [[$ \Delta E_\text{P}=W=Gh=mgh $]]. Jos etäisyyden muutos on pidempi kuin muutamia kilometrejä, ei gravitaatiokenttää voida enää tarkastella homogeenisena. Gravitaatiovoiman ja siten myös siirtämiseen vaaditun voiman suuruus muuttuu alku- ja loppupisteiden välillä. Voiman suuruus saadaan gravitaatiolaista. Tehty työ eli potentiaalienergian muutos voidaan määrittää voima–paikka-kuvaajan pinta-alana, eli integraalina paikan suhteen.
Potentiaalienergia gravitaatiokentässä
[[$ \quad E_\text{P}=-\gamma \dfrac{Mm}{r} $]]
missä [[$ \gamma $]] on gravitaatiovakio, M ja m ovat gravitaatiokentän synnyttävän kappaleen ja gravitaatiokentässä liikkuvan kappaleen massat sekä r kentässä liikkuvan kappaleen etäisyys kentän luoneen kappaleen keskipisteestä.
Mekaanisen energian säilymislain mukaan liike- ja potentiaalienergian summa ei muutu, jos kappaleeseen vaikuttavat vain konservatiiviset voimat. Mekaanisen energian säilymistä ja konservatiivisia voimia käsiteltiin kurssilla FY4. Voimaa kutsuttiin konservatiiviseksi, jos sitä vastaan tehty työ varastoitui kappaleen potentiaalienergiaksi. Gravitaatio on tällainen voima, ja näin ollen taivaankappaleen mekaaninen energia säilyy sen liikkuessa avaruudessa pelkän gravitaation vaikutuksen alaisena.
Mekaanisen energian säilyminen gravitaatiokentässä
[[$ \quad E_\text{K}+E_\text{P}=\textrm{vakio} $]]
[[$\quad \frac{1}{2}mv^2-\gamma\dfrac{mM}{r}=\textrm{vakio}$]]
missä [[$ \gamma $]] on gravitaatiovakio, [[$M$]] ja [[$m$]] ovat gravitaatiokentän synnyttävän kappaleen ja gravitaatiokentässä liikkuvan kappaleen massat, [[$v$]] kentässä liikkuvan kappaleen nopeus sekä [[$r$]] kentässä liikkuvan kappaleen etäisyys kentän luoneen kappaleen keskipisteestä.
Mekaanisen energian säilymislain mukaan potentiaalienergian pieneneminen kasvattaa liike-energiaa. Mekaanisen energian säilymislaki ilmenee esimerkiksi taivaankappaleiden ellipsiradoilla. Maa kiertää Aurinkoa lievästi elliptisellä radalla. Ollessaan kauempana Auringosta potentiaalienergia on hieman suurempi ja liike-energia vastaavasti pienempi, joten Maa liikkuu hitaampaa vauhtia kuin Aurinkoa lähempänä ollessaan.
| Potentiaalienergia | Liike-energia |
|---|---|
| Kappaleen potentiaalienergia kasvaa, kappale liikuu kauemmas gravitaatiokentän aiheuttajasta (ellipsirata) | Kappaleen liike-energia pienenee, kappaleen nopeus pienenee |
| Kappaleen potentiaalienergia pienenee, kappale liikkuu lähemmäs gravitaatiokentän aiheuttajaa (ellipsirata) | Kappaleen liike-energia kasvaa, kappaleen nopeus suurenee |
| Potentiaalienergia ei muutu, kappaleen etäisyys graviaatiokentän aiheuttajasta ei muutu (ympyrärata) | Kappaleen liike-energia ei muutu, kappale liikku tasaisella vauhdilla |
Yleisen gravitaatiolain käyttö on käytännöllistä, jos kappale liikkuu ympyräradalla. Silloin gravitaatiovoima pysyy vakiona. Jos elliptisyys pitää ottaa huomioon tai jos tutkittavassa tilanteessa tarkasteltavan kappaleen etäisyys gravitaatiokentän keskipisteestä muuten muuttuu, on hyödyllistä soveltaa mekaanisen energian säilymistä. Sen heikkoutena on kuitenkin, että liike-energialla ei ole suuntaa, joten lailla ei pysty selvittämään kappaleen nopeuden suuntaa, ainoastaan suuruuden.
| Yleinen gravitaatiolaki | Kappale liikkuu ympyräradalla eli etäisyys gravitaatiokentän aiheuttajasta ei muutu |
| Mekaanisen energian säilyminen | Kappale liikkuu ellipsin muotoisella radalla eli etäisyys graviaatiokentän aiheuttajasta muuttuu |