3.1 Liike
Suureita ja määritelmiä
| Suure ja määritelmä | Määritys kuvaajasta |
|---|---|
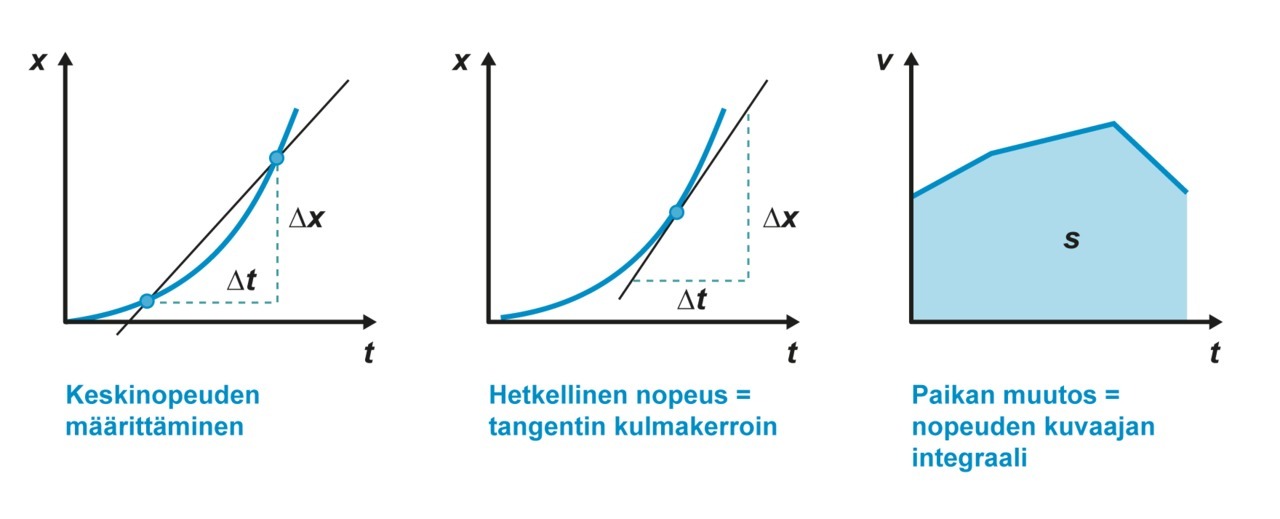
| Siirtymä eli paikan muutos, [[$\Delta x=x_2-x_1$]] | [[$(t,v)$]]-kuvaajan fysikaalinen pinta-ala eli integraali |
| Matka [[$s$]] on siirtymän itseisarvo samaan suuntaan etenevässä liikkeessä. Matka on aina positiivinen. | [[$(t, \left|v\right|)$]]-kuvaajan fysikaalinen pinta-ala |
| Nopeus, [[$v$]], on paikan muutos ajan suhteen, [[$v=\dfrac{\Delta x}{\Delta t}$]] | [[$(t,x)$]]-kuvaajassa kulmakertoimen arvo |
| Keskinopeus, [[$v_k$]], on määritetyllä aikavälillä tapahtuva paikan muutos, [[$v_k=\dfrac{\Delta x}{\Delta t}=\dfrac{x_2-x_1}{t_2-t_1}$]] | [[$(t,x)$]]-kuvaajassa tarkasteluvälin pisteiden välille piirretyn suoran kulmakerroin (lasketaan taulukkoarvoista jos mahdollista) |
| Hetkellinen nopeus, [[$v$]], on nopeus tietyllä ajanhetkellä, [[$v=\dfrac{dx}{dt}$]] | [[$(t,x)$]]-kuvaajassa tarkasteluhetkellä kuvaajan tangentin kulmakerroin |
| Vauhti, [[$v$]], on nopeuden suuruus, ei huomioi nopeuden suuntaa, [[$|v|=\dfrac{ds}{dt}$]] | |
| Tasainen nopeus, [[$v$]], on nopeus, jonka suuruus ja suunta eivät muutu | [[$(t,x)$]]-kuvaajassa suoran kulmakertoimen suuruus |
| Tasainen vauhti, [[$v$]], on nopeus, jonka suuruus ei muutu | |
| Nopeuden muutos, [[$\Delta v$]], on loppu- ja alkunopeuden erotus, [[$\Delta v=v_2-v_1$]] | [[$(t,a)$]]-kuvaajan fysikaalinen pinta-ala eli integraali |
| Kiihtyvyys, [[$a$]], on nopeuden muutos ajan suhteen, [[$a=\dfrac{dv}{dt}$]] | [[$(t,v)$]]-kuvaajassa kulmakertoimen arvo |
| Keskikiihtyvyys, [[$a_k$]], on määritetyllä aikavälillä tapahtuva nopeuden muutos, [[$a_k=\dfrac{\Delta v}{\Delta t}=\dfrac{v_2-v_1}{t_2-t_1} $]] | [[$(t,v)$]]-kuvaajassa tarkasteluvälin pisteiden välille piirretyn suoran kulmakerroin (lasketaan taulukkoarvoista, jos mahdollista) |
| Hetkellinen kiihtyvyys, [[$a$]], on kiihtyvyys tietyllä ajanhetkellä, [[$a=\dfrac{dv}{dt}$]] | [[$(t,v)$]]-kuvaajassa tarkasteluhetkellä kuvaajan tangentin kulmakerroin |
| Tasainen kiihtyvyys, [[$a$]], on kiihtyvyys, jonka suuruus ja suunta eivät muutu | [[$(t,v)$]]-kuvaajassa suoran kulmakertoimen suuruus |
| Putoamiskiihtyvyys, [[$g$]], on kiihtyvyys, jolla kappaleet aloittavat putoamisen maanpinnan läheisyydessä ilman, että ilmanvastus vaikuttaa putoamiseen |
Liikkeen kuvaajat ja niiden analyysi
Liikkeen matemaattiset mallit ja laskukaavat
Edellä esiteltiin liikkeen suureiden määritelmiä ja niiden määrityttämistä graafisesti. Täysin laskennallisissa tehtävissä hyödynnetään kahta liikkeen mallia: tasaisen liikkeen mallia sekä tasaisesti kiihtyvän liikkeen mallia.
Tasaisessa liikkeessä nopeus on vakio. Liikkeen voidaan valita etenevän positiiviseen suuntaan, jolloin siirtymä on sama kuin kuljettu matka.
Tasaisesti kiihtyvässä liikkeessä kiihtyvyys on vakio. Nopeus alussa riippuu tilanteesta. Nopeus ja kiihtyvyys voivat olla negatiivisia tai positiivisia riippuen valitusta suunnasta. Usein voidaan valita paikaksi alussa origo.
Tasainen liike
Matka tasaisessa liikkeessä
[[$\quad s=vt$]]
Tasaisesti kiihtyvä liike
Nopeus ja paikka tasaisesti kiihtyvässä liikkeessä
[[$\begin{align*} \quad v&=v_0+at \\ x&=x_0+v_0t+\dfrac{1}{2}at^2 \end{align*}$]]
Keskinopeus on alku- ja loppunopeuden keskiarvo
[[$\begin{align*} \quad v_k&=\dfrac{v_0+v}{2}\end{align*}$]]