Esimerkkitilanteita
Satelliitin liike taivaankappaleen ympäri
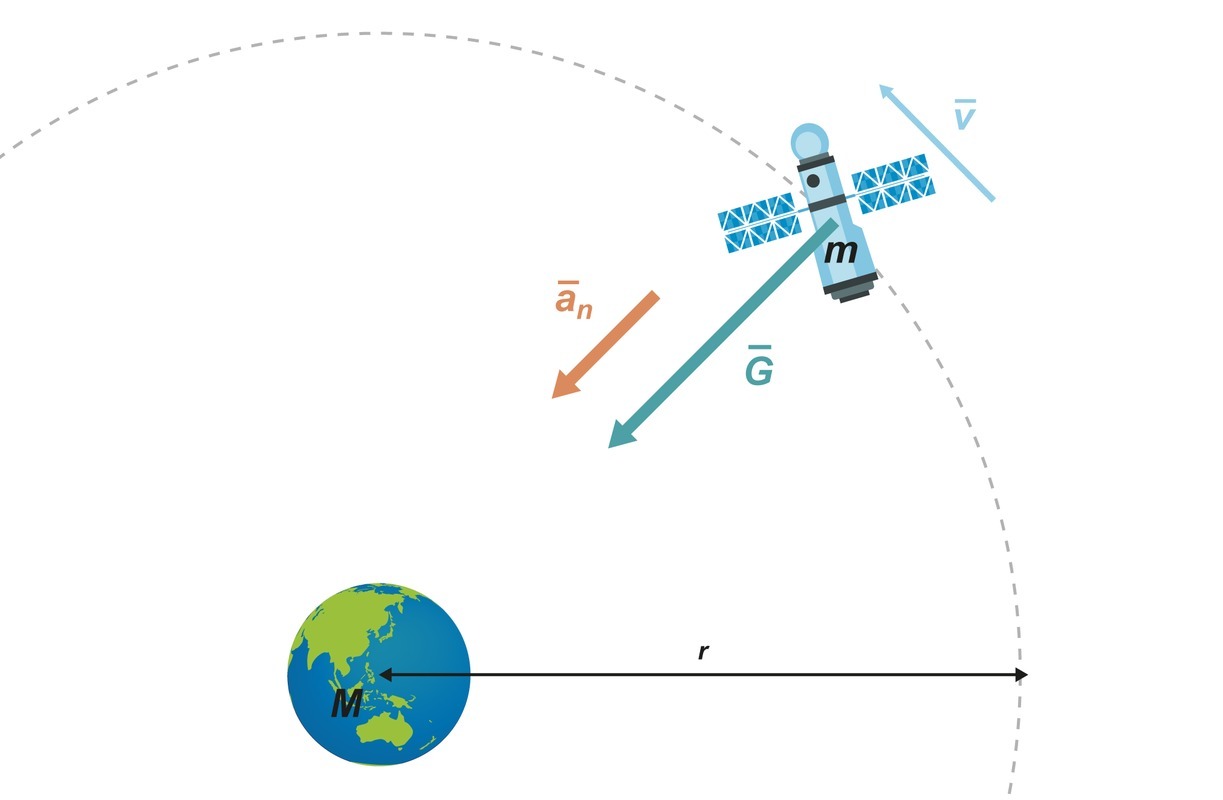
Satelliitin liikkeestä taivaankappaleen ympäri voidaan kirjoittaa liikeyhtälö. Ainoa satelliittiin vaikuttava voima on gravitaatio (G). Liike on tasaista ympyräliikettä, jossa normaalikiihtyvyys (an) on kohti radan keskipistettä. Tilanteen voimakuvio on ohessa.
Muodostetaan dynamiikan peruslain mukainen liikeyhtälö satelliitille.
[[$ \begin{align*} \quad \Sigma \overline{F}&=m\overline{a} \\ \, \\ \overline{G}&=m\overline{a} \\ \, \\ G&=ma_n \\ \end{align*} $]]
Sijoitetaan yhtälöön gravitaatiovoiman paikalle sen määritelmän mukainen lauseke. Pienen kiertävän kappaleen (satelliitti) massaa merkitään usein pienellä [[$m$]]-kirjaimella ja taivaankappaleen (esimerkiksi Maa) massaa isolla [[$M$]]-kirjaimella. Gravitaatiolain etäisyys tarkoittaa kappaleiden massakeskipisteiden välistä etäisyyttä. Saadaan liikeyhtälö
[[$ \quad \gamma\dfrac{mM}{r^2}=ma_n $]].
Tästä voidaan ratkaista mitä tahansa satelliitin liikkeeseen liittyviä suureita.
Kiihtyvyys
Jakamalla liikeyhtälö puolittain satelliitin massalla saadaan sen kiihtyvyydelle lauseke.
[[$\quad a_n=\gamma\dfrac{M}{r^2} $]]
Nähdään, että satelliitin kiihtyvyys kiertoradalla ei riipu satelliitin massasta. Sen sijaan taivaankappaleen massa ja kappaleiden välinen etäisyys vaikuttavat kiihtyvyyden suuruuteen.
Nopeus
Satelliitin nopeus voidaan ratkaista liikeyhtälöstä soveltaen normaalikiihtyvyyden ympyrärataehtoa: [[$ a_n=\dfrac{v^2}{r}.$]] Saadaan
[[$\begin{align*} \quad \gamma \dfrac{mM}{r^2}&=m\dfrac{v^2}{r} \\ \, \\ \gamma \dfrac{M}{r}&=v^2 \\ \, \\ v&=\sqrt{\gamma\dfrac{M}{r}} \\ \end{align*}$]]
Tästä nähdään, että satelliitin nopeus riippuu sen etäisyydestä taivaankappaleen massakeskipisteestä sekä taivaankappaleen massasta. Yhtälöstä voidaan päätellä, että säteen kasvaessa satelliitin vauhti hidastuu.
Kiertoaika
Satelliitti liikkuu ympyräradalla tasaisella vauhdilla. Kiertoajan T lauseke saadaan, kun on määritetty yhden kierroksen pituus ja ratanopeus: [[$ v=\dfrac{s}{t}=\dfrac{2\pi r}{T}.$]] Sijoittamalla tämä lauseke aiempaan liikeyhtälöön voidaan ratkaista kiertoaika. Saadaan
[[$\begin{align*} \gamma \dfrac{M}{r}&=v^2 \\ \, \\ \gamma \dfrac{M}{r}&=\left(\dfrac{2\pi r}{T}\right)^2 \\ \, \\ \gamma \dfrac{M}{r}&=\dfrac{4\pi^2 r^2}{T^2} \\ \, \\ \quad T^2\gamma M&=4\pi^2 r^3 \\ \, \\ T^2&=\dfrac{4\pi^2 r^3}{\gamma M} \\ \end{align*}$]]
Ottamalla tästä vielä neliöjuuri saadaan kiertoajalle lauseke, joka riippuu taivaankappaleen massasta ja etäisyydestä. Tämä on kuuluisa Keplerin 3. laki, joka ilmaisi kiertoajan ja etäisyyden välisen riippuvuuden.
[[$\quad T=\sqrt{\dfrac{4\pi^2 r^3}{\gamma M}}$]]
Halleyn komeetta
Halleyn komeetta on yksi tunnetuimmista aurinkokunnan pienkappaleista. Komeetta kiertää Aurinkoa ellipsin muotisella radalla, jonka kaukaisin etäisyys on 35,3 AU. Lähimmillään Aurinkoa komeetta on etäisyydellä 0,587 AU liikkuen nopeudella 54,6 km/s. Kuinka suuri on komeetan nopeus kiertoratansa kaukaisimmassa pisteessä?
RatkaisuKomeetan liikkuessa Auringon ympäri sen mekaaninen energia säilyy. Energia muuttaa muotoaan potentiaali- ja liike-energian välillä. Energiaperiaatteesta saadaan yhtälö [[$ E_\text{K1}+E_\text{P1}=E_\text{K2}+E_\text{P2}$]]. Sijoitetaan yhtälöön liike-energian lauseke [[$E_\text{K}=\dfrac{1}{2}mv^2$]] ja gravitaatiopotentiaalienergian lauseke [[$E_\text{P}=-\gamma\dfrac{mM}{r}$]], yhtälö tulee muotoon
[[$ \quad \dfrac{1}{2}mv_1^2-\gamma\dfrac{mM}{r_1}=\dfrac{1}{2}mv_2^2-\gamma\dfrac{mM}{r_2}$]]
Tiedossa olevat lukuarvot ovat:
[[$ v_1=54\,600\textrm{ m/s} \\ \gamma = \text{6,6742}\cdot 10^{-11}\dfrac{\text{Nm}^2}{\text{kg}^2} \\ M=\text{1,989}\cdot 10^{30} \textrm{ kg} \\ r_1=\text{0,587}\cdot \text{1,496}\cdot 10^{11} \textrm{ m}=\text{8,78152}\cdot 10^{10}\text{ m} \\ r_2=\text{35,3}\cdot \text{1,496}\cdot 10^{11} \textrm{ m}=\text{5,28088}\cdot 10^{12}\text{ m} $]]
Kaikki muut suureet yhtälössä tunnetaan paitsi kysytty nopeus [[$v_2$]].
[[$ \begin{align*}\quad \dfrac{1}{2}mv_1^2-\gamma\dfrac{mM}{r_1}&=\dfrac{1}{2}mv_2^2-\gamma\dfrac{mM}{r_2} \\ \, \\ \dfrac{1}{2}v_1^2-\gamma\dfrac{M}{r_1}&=\dfrac{1}{2}v_2^2-\gamma\dfrac{M}{r_2} \\ \,\\ \dfrac{1}{2}v_2^2&=\dfrac{1}{2}v_1^2-\gamma\dfrac{M}{r_1}+\gamma\dfrac{M}{r_2} \\ \, \\ v_2^2&=v_1^2-2\gamma \left(\dfrac{M}{r_1}-\dfrac{M}{r_2}\right) \\ \, \\ v_2&=\sqrt{v_1^2-2\gamma \left(\dfrac{M}{r_1}-\dfrac{M}{r_2}\right)} \\ \, \\ v_2&=\sqrt{\left(54\,600\textrm{ m/s}\right)^2-2\cdot\text{6,6742}\cdot 10^{-11}\dfrac{\text{Nm}^2}{\text{kg}^2}\cdot \left(\dfrac{\text{1,989}\cdot 10^{30} \textrm{ kg}}{\text{8,78152}\cdot 10^{10}\text{ m}}-\dfrac{\text{1,989}\cdot 10^{30} \textrm{ kg}}{\text{5,28088}\cdot 10^{12}\text{ m}}\right)} \\ \, \\ &=\text{2 836,3}\ldots \textrm{ m/s}\approx \text{2,8 km/s} \\ \end{align*} $]]
Komeetan nopeus kiertoratansa kaukaisimmassa pisteessä on 2,8 km/s.