FY6S
5.
5-4
a) Magnetointi tarkoittaa magnetoituvan aineen tekemistä magneettiseski.
b) Rautanaulan voi magnetoida, koska rauta on magnetoituva aine.
c) Ohut rautanaula muuttuu magneettiseksi, kun sitä sivellään kestomagneetilla useita kertyoja saman suuntaisin vedoin, Sivelyjä joutuu tekemään sitä enemmän, mitä paksumpi rautanaula on.
d) Magneettisuus voidaan poistaa rautanaulasta esimerkiksi kuumentamalla tai sopivasti lyömällä. Pudostus voi myös aiheuttaa magneettisuuden heikkenemisen.
e) Kuparia ei voi magnetoida, koska kupari ei ole magnetoituva aine.
f) Kestomagneetin magneettisuuden voi poistaa esimerkiksi takomalla, kuumentamalla aine Curie-lämpötilaan tai viemällä magneetti pitkäksi ajaksi vaihtovirtaan kytketyn käämin sisään.
5-5
a) Magneetin magneettisuus säilyy vuosia, mutta sähkömagneetin magnmeettisuus voidaan kytkeä päälle ja pois päältä tarpeen mukaan.
b) Sähkömagneetti koostuu virtapiiristä, jossa on tasajännitelähde, käämi ja käämillä rautasydän. Kun sähkömagneettiin kytketään sähkövirta, sähkömagneetin ympärille muodostuu magneettikenttä, jkoka saa rautaromun tarttumaan magneettiin. Kenttä on voimakkain käämin päissä. Kun sähkövirta katkaistaan, magneettkenttä ei ole, jolloin rautaromu irtoaa magneetista.
c) Sähkömagneetteja käyutetään mm. nostureissa, kaiuyyiomissa, mikrofoneissa ja ovien sähkölukoissa.
d) Nosturilla voidaan nostaa vain sellaisia kappaleita, joissa on rautaa.
5-6
a) Oikein
b) Väärin. Magneetti on dipoli, eli sillä on aina kaksi kohtiota: kohtiota ei voi erottaa toisistaan, koska magneettisuus on peräisin aineen mirkorakenteesta.
c) Oikein
d) Väärin. Magnetoituvia metalleja ovat rauta, koboltti ja nikkeli
e) Oikein
f) Oikein
4.
4-5
a) Hilan hilavakio saadaan hilayhtälöstä

 , josta tulee kulmalle arvo
, josta tulee kulmalle arvo 
 , josta saadaan taipumiskulmalle arvo
, josta saadaan taipumiskulmalle arvo 
 , josta saadaan kulmalle arvo
, josta saadaan kulmalle arvo 

a) Hilan hilavakio saadaan hilayhtälöstä
b) Lasketaan kolmannen kertaluvun (k=3) taipumiskulma. Hilayhtälöstä  seuraa yhtälö
seuraa yhtälö
4-8
Hilan hilavakio on  . Hilayhtälöstä
. Hilayhtälöstä  saadaan yhtälö
saadaan yhtälö  .
.
Ensimmäisen intensiteetti maksimin tapauksessa on
Etäisyys keskikohdasta on 
Toisen intensiteettimaksimin tapauksessa on
Etäisyys keskikohdasta on 
Intensiteettimaksimien etäisyys on
4-12
Hilayhtälön mukaan pienin taipumiskulma vastaa pienintä k:n arvoa eli k=1. Hilan hilavakioksi eli hilarakojen etäisyydeksi stoisistaan saadaan
mukaan pienin taipumiskulma vastaa pienintä k:n arvoa eli k=1. Hilan hilavakioksi eli hilarakojen etäisyydeksi stoisistaan saadaan 
Rakojen lukumäärä millimetrillä on 
3.
3-1
a, c
3-2
Kappaleen näkyminen johtuu siitä, että kappale heijastaa valoa. Väri aiheutuu kappaleen pinnassa tapahtuvan valon absorption ja heijastumisen keskinnäisestä suhteesta. Jos kappale absorboi valoisesta valosta vihreän allonpituuden, kappale nähdään punaisena, Silmä näkee jäljelle jääneen valon aallonpituudet (spektrin) ja tulkitsee sen punaiseksi. Kappaleesta heijastuneet valkoisen valon aallon pituudet määrävät kappaleen värin.
a) Jos aine imee lähes kaiken siihen osuvan valon, se ei heijasta valoa kovin paljon ja se näyttää tummalta. Silmä erottaa värit vain, jos valon intensiteetti on tarpeeksi suuri.
b) Aine, joka heijastaa lähes kaiken siihen osuvan valon, heijastaa kaikkia valon sisältämiä aallonpituuksia, Absorptio on vähäistä. Silloin aineen pinta näyttää valoisessa valossa, esimerkiksi auringon valossa, valoiselta.
c)Punaiset kengät näyttävät sinisessä valossa mustilta, Punainen pinta absorboi tehokkaasti sinisiä aallonpituuksia, ja sen takia punainen kenkä ei heijsat sinisessä valistuksessa valoa lainkaan eli on musta.
3-5
Valon taittumislaista  saadaan
saadaan
Vastavaasti
Kulmien ero on
1.
1-2




a)
b)
c)
d)
Mittausohjelman avulla mittauspisteisiin tehty lineaarinen sovitys antaa suoran, jonka fysikaalinen kulmakerroin on 0,2834 m/ns. Valonnopeus on tämä kulmakerroin eli .
.
1-8
Sen, ovatko aurinkolasit polarisoivat, voi trakistaa esimerkiksi seuraavasti:-Takastellaan pöydän pinnasta viosti heijastunutta valoa kääntelemällä aurinkolaseja eri asentoihin. Jos valon kirkkaus muuttuu lasien asentoa muutettaessa, lasit ovat polarisoivat.
-Katsotaan siunistä taivasta eri asennoissa olevien lasien läpi, jos taivaan kirkkaus muuttuu tummaksi jossain lasien asennossa, lasit ovat polarisoivat.
-Käännellään laseja tietokoneen näytön edessä. Jos kuva muuttuu tummaksi jossain lasien asennossa, lasit ovat polarisoivat.
16. Vaihtovirta
16-2


![f_0=\frac{1}{2\pi\sqrt[]{LC}}=\frac{1}{2\pi\sqrt[]{10{,}0\cdot10^{-3}H\cdot2{,}0\cdot10^{-9}F}}=35588{,}12717F\approx36kHz](https://math-demo.abitti.fi/math.svg?latex=f_0%3D%5Cfrac%7B1%7D%7B2%5Cpi%5Csqrt%5B%5D%7BLC%7D%7D%3D%5Cfrac%7B1%7D%7B2%5Cpi%5Csqrt%5B%5D%7B10%7B%2C%7D0%5Ccdot10%5E%7B-3%7DH%5Ccdot2%7B%2C%7D0%5Ccdot10%5E%7B-9%7DF%7D%7D%3D35588%7B%2C%7D12717F%5Capprox36kHz)


![f_0=\frac{1}{2\pi\sqrt[]{LC}}](https://math-demo.abitti.fi/math.svg?latex=f_0%3D%5Cfrac%7B1%7D%7B2%5Cpi%5Csqrt%5B%5D%7BLC%7D%7D)
![\sqrt[]{LC}=\frac{1}{2\pi f_0}](https://math-demo.abitti.fi/math.svg?latex=%5Csqrt%5B%5D%7BLC%7D%3D%5Cfrac%7B1%7D%7B2%5Cpi%20f_0%7D)
%5E2)
%5E2%7D%7BL%7D%3D%5Cfrac%7B%5Cleft(%5Cfrac%7B1%7D%7B2%5Cpi%5Ccdot97%7B%2C%7D7%5Ccdot10%5E6Hz%7D%5Cright)%7D%7B15%5Ccdot10%5E%7B-3%7DH%7D%3D)


a) 1921
b) 1955
c) 1984
d) 1977
e) 1995
f) 2002
g) 2002
16-3
16-4
16-5
a) Taajuus on
b) Nopeuis on v=s/t, joten aika on
16-10
Tiivistelmään pitää sisältyä ainakin seuraavat asiat:
Tiivistelmään pitää sisältyä ainakin seuraavat asiat:
a) Kantoaalto on vakiotaajuinen ja -amplitudinen sähkömagneettinen aalto, jota esimerkiksi radioasema lähettää.
b) Kantoaallon moduloinnilla kantoaalto saadaan välittämään tietoa.
c) Modulointi suoritetaan muuttelemalla kantoaallon taajuutta tai amplitudia.
15. Muuntaja ja energian siirto
15-2












b, d
15-3
15-4
Kuinka suuri on toisiopuolen jännite?
Kuinka suuri on toisiopuolen jännite?
Videolla on annettu tiedot ,
,  ja
ja . Oletetaan muuntajan tehohäviöt pieniksi, jolloin voidaan käyttää ideaalisen muuntajan muuntosuhteen yhtälöä
. Oletetaan muuntajan tehohäviöt pieniksi, jolloin voidaan käyttää ideaalisen muuntajan muuntosuhteen yhtälöä . Tästä saadaan toisiopuolen jännitteeksi
. Tästä saadaan toisiopuolen jännitteeksi
Mikä on valokaari?
Kun kahden elektrodin välillä on suuri sähkökenttä, elektrodien välissä olevan ilman molekyylit ionisoituvat vuorovaikuttaessaan kentän suurienergisten fotonien kanssa ja ilma alkaa johtaa sähköä. Ilmaan muodostuu sähköä johtava kanava, jossa ilma kuumenee voimakkaasti ja lähettää kirkasta valoa. Tätä sanotaan valokaareksi.
Miksi junanvaunun päälle kiipeäminen on kielletty?
Sähköradan ajojohtimissa on 25 kV:n jännite. Junanvaunun katolla ollessaan ihminen on sähköisesti kytkettynä maahan eli hän on nollapotentiaalissa. Ihmisen ja ajojohtimen välillä on sillo
15-5
15-6

a) Mallinnetaan muuntajaa ideaalisella muuntajalla. Koska kierrosten määrä on ensiöpuolella satakertainen toisiopuoleen verrattuna, toisiojännite on yhtälön  perusteella sadasosa ensiöjännitteestä ja toisiopuolen sähkövirta on satakertainen ensiöpuolen sähkövirtaan verrattuna eli
perusteella sadasosa ensiöjännitteestä ja toisiopuolen sähkövirta on satakertainen ensiöpuolen sähkövirtaan verrattuna eli .
.
b) Kuumennusteho on kääntäen verrannollinen resistanssiin. Hehkulangan resistanssi on suuri, joten langan läpimenevä virta on pieni. Sähkövirta kuumentaa hehkulankaa teholla  . Lampun hehkulanka kuumenee hehkuvaksi, mutta volframi, josta hehkulanka on valmistettu, on kuumana erittäin kovaa, toisin kuin esimerkiksi naulan valmistusaine rauta. Sen takia hehkulanka ei katkea kuumetessaan.
. Lampun hehkulanka kuumenee hehkuvaksi, mutta volframi, josta hehkulanka on valmistettu, on kuumana erittäin kovaa, toisin kuin esimerkiksi naulan valmistusaine rauta. Sen takia hehkulanka ei katkea kuumetessaan.
15-6
a) Mallinnetaan muuntajaa ideaalisella muuntajalla. Oikea vaihtoehto on 1) 3,3 V. Jännitteiden suhde on kääntäen verrannollinen sähkövirtojen suhteeseen eli  , joten ensiöpuolen jännite on
, joten ensiöpuolen jännite on 
b) Muutosuhde on
14. Vaihtovirta
14-1
Tasavirtaa saadaan paristosta tai tasajännitelähteestä. Tasavirtapiirissä tasavirran suunta on pariston (jännitelähteen) positiiviselta navalta negatiiviselle navalle. Niin kauan kuin pariston jännite pysyy vakiona, sähkövirran suuruus on virtapiirissä vakio.
Vaihtovirtaa saadaan vaihtojännitelähteestä. Vaihtovirtapiirissä sähkövirran suuruus ja suunta vaihtelevat jaksollisesti. Generaattorilla tuotettu vaihtovirta on sinimuotoista.
14-3
a) 4,0V
b) ![U=\frac{u_0}{\sqrt[]{2}}=\frac{4{,}0V}{\sqrt[]{2}}=2\sqrt[]{2}V=2{,}828...\approx2{,}8V](https://math-demo.abitti.fi/math.svg?latex=U%3D%5Cfrac%7Bu_0%7D%7B%5Csqrt%5B%5D%7B2%7D%7D%3D%5Cfrac%7B4%7B%2C%7D0V%7D%7B%5Csqrt%5B%5D%7B2%7D%7D%3D2%5Csqrt%5B%5D%7B2%7DV%3D2%7B%2C%7D828...%5Capprox2%7B%2C%7D8V)
c) 0,020s
d) 
14-4
a)
b)
c)
d)
14-5
![I=\frac{i_0}{\sqrt[]{2}}=\frac{0{,}495A}{\sqrt[]{2}}\approx0{,}35A](https://math-demo.abitti.fi/math.svg?latex=I%3D%5Cfrac%7Bi_0%7D%7B%5Csqrt%5B%5D%7B2%7D%7D%3D%5Cfrac%7B0%7B%2C%7D495A%7D%7B%5Csqrt%5B%5D%7B2%7D%7D%5Capprox0%7B%2C%7D35A)

a) Vaihtovirran ) kuvaaja
kuvaaja
b) Vaihtovirran huippuarvo on  ja tehollinen arvo
ja tehollinen arvo
c) Koska vaihtovirran yhtälö on %3D0%7B%2C%7D495A%5Ccdot%5Csin%5Cleft(2%5Cpi%5Ccdot40t%5Cright)) vasihtovirran taajuus on 40Hz
vasihtovirran taajuus on 40Hz
![u_0=U\sqrt[]{2}=230V\cdot\sqrt[]{2}\approx330V](https://math-demo.abitti.fi/math.svg?latex=u_0%3DU%5Csqrt%5B%5D%7B2%7D%3D230V%5Ccdot%5Csqrt%5B%5D%7B2%7D%5Capprox330V)
d) Vaihtovirran arvot saadaan joko katsomalla kuvaajasta tai laskemalla vaihtovirran yhtälöstä. Vaihtovirran arvot hetkellä  = 23 ms on -0,24 A ja hetkellä
= 23 ms on -0,24 A ja hetkellä  = 36 ms 0,18 A
= 36 ms 0,18 A
14-6
a) Vaihtojännitteen tehollinen arvo on ![U=\frac{u_0}{\sqrt[]{2}}](https://math-demo.abitti.fi/math.svg?latex=U%3D%5Cfrac%7Bu_0%7D%7B%5Csqrt%5B%5D%7B2%7D%7D) , jolloin jänniteen huippuarvo on
, jolloin jänniteen huippuarvo on
b) Laitetta ei voida kytkeä sähköverkkoon, koska sen jännitteenkesto (290 V) on pienempi kuin sähköverkon hetkellinen maksimijännite (330 V).
c) Huippuarvo on suurempi kuin tehollinen arvo. Jännitteen huippuarvo on suurin laitteeseen tai kytkentään vaikuttava jännite laitteen käytön aikana.
14-7
a) Indusoitavan jännitteen huippuarvo on
a) Indusoitavan jännitteen huippuarvo on
b) Sähkövirran huippuarvo on 
14-8
a)
Jännitteen huippuarvo on 
Tästä saadaan resistanssi
b)
Vastuksen tuottama energia on 
Vastuksen tuottama teho on  , jossa
, jossa
Vastuksen tuottama lämpömäärä on
Vastuksen hetkellinen jännitehäviö, kun 
14-9
a) Laitteen sähköteho on P=UI ja jännitehäviön tehollinen arvo U=RI, jota 
Vaihtovirran tehollinen arvo
tai
Kpl.12
12-1




 Magneettivuo ajan funktiona on
Magneettivuo ajan funktiona on
%3DA%5Cperp%20B%3DA%5Ccos%5Calpha%5Ccdot%20B%3DA%5Ccos%5Comega%20t%5Ccdot%20B%3D0%7B%2C%7D624m%5E2%5Ccdot0%7B%2C%7D42T%5Ccdot%5Cleft(480%5Cpi%5Ccdot%5Cfrac%7B1%7D%7Bs%7Dt%5Cright)%5Capprox0%7B%2C%7D26208Wb%5Ccdot%5Ccos%5Cleft(1507%7B%2C%7D96%5C%20%5Cfrac%7B1%7D%7Bs%7Dt%5Cright))
%7D%7Bdt%7D%3DNAB%5Comega%5Csin%5Comega%20t) Jännite ajan funktiona on
Jännite ajan funktiona on
%3DNAB%5Comega%5Csin%5Comega%20t%3D6718%7B%2C%7D52%5Ccdot%5Csin%5Cleft(1507%7B%2C%7D96%5Ccdot%5Cfrac%7B1%7D%7Bs%7Dt%5Cright)) d) Kun magneettivuo saa itseisarvoltaan suurimman arvonsa, niin jännite saa pienimmän arvonsa.
d) Kun magneettivuo saa itseisarvoltaan suurimman arvonsa, niin jännite saa pienimmän arvonsa.
a) Pyörrevirroilla tarkoitetaan sähkövirtoja, jotka syntyvät muuttuvassa magneettikentässä olevaan metallikappaleeseen. Ne aiheuttavat magneettikentän, joka pyrkii heikentämään kasvavaa ulkoista magneettikenttää ja vahvistamaan pienenevää ulkoista magneettikenttää
b) Ei voi syntyä. Pyörrevirrat syntyvät metallikappaleessa aina sellaiseen alueeseen, jossa magneettikentän magneettivuo muuttuu. Tämä muutos voi aiheutua joko kappaleen liikkeestä tai magneettikentän muutoksesta (magneetti voi liikkua kappaleen suhteen).
c) Pyörrevirrat aiheuttavat tehohäviöitä mm. generaattoreissa, moottoreissa ja muuntajien rautasydämissä, koska pyörrevirtojen takia osa energiasta muuntuu esimerkiksi muuntajan rautasydämen sisäenergiaksi eli rautasydän lämpenee.
d) Esimerkiksi muuntajan rautasydämen voi valmistaa useista eristetyistä liuskoista, samoin metallin kokonaispinta-alaa voi voi joissakin tapauksissa pienentää tekemällä levystä kampamaisen.
12-3
a) Magneetti vierii nopeammin muovilla kuin alumiinilla, koska muovi on eriste.
b) Teräskuullat vierivät kahdella levyllä yhtä nopeasti.
13-7
a)
Magneettivuo muuttuu jaksollisesti, koska pyörii tasaisella kulmanopeudella
b) Induktiolain mukaan lähdejännite on
12-5
Induktioliesissä pyörrevirrat kuumentavat suoraan liedelle asetetun metallikattilan pohjaa. Lieden keraaminen pinta johtaa huonosti lämpöä lieden muihin osiin, joten energiaa menee vain vähän hukkaan. Induktiolevyn pinta ei kuumene yhtä paljon kuin metalliset sähkölevyt. Ruokien kuumentaminen induktioliedellä edellyttää metallisten astioiden käyttöä, koska pyörrevirtojen syntyminen edellyttää materiaalilta hyvää sähkönjohtavuutta.
Vaikka teoriassa keittolevyillä olisi mahdollista käyttää myös muita kuin metallisia keittoastioita, lasin ja keramiikan huonon lämmönjohtavuuden ja rikkoutumisvaaran vuoksi kaikki liedelle suunnitellut astiat ovat metallisia, joten induktioliesi ei tässäkään mielessä ole perinteistä lämmön johtumiseen perustuvaa liettä huonompi. Induktioliesien etuja ovat myös nopeus ja hyvä säädettävyys. Induktioliesien energiankulutus on pienempi kuin perinteisten liesien.
13-1
a) i) Silmukan läpi kulkeva magneettivuo on suurin piirroksessa 3. ii) Silmukan läpi kulkeva magneettivuo on pienin piirroksessa 1.
b) i) Lähdejännite on suurin piirroksessa 1. ii) Lähdejännite on pienin (nolla) piirroksessa 3.
13-2
Kohdassa a lähdejännite saavuttaa huippuarvonsa, koska käämin silmukoiden taso on magneettikentän suuntainen (käämin magneettikentän kenttäviivat ovat kohtisuorassa ulkoista magneettikenttää vastaan).
Kohdassa b lähdejännite on nolla, koska käämin silmukoiden taso on kohtisuorassa magneettikenttää vastaan (käämin magneettikentän kenttäviivat ovat samansuuntaiset ulkoisen magneettikentän kanssa).
Kohdassa c lähdejännite kasvaa, joten käämin silmukoiden taso on vinossa magneettikenttää vastaan.
13-5
a) Pyörimisnopeuden kasvattamien lisää vaihtojännitteen taajuutta. Jännitteen suuruuteen vaikuttavat magneettivuon tiheys, käämin pintaala ja kulmanopeus (ja käämin kierrosmäärä, tässä tehtävässä N=1).
b) Koska jaksonaika on 0,020 s = 20 ms, jännitteen taajuus on . Silmukan pyörimisnopeus on 50 r/s.
. Silmukan pyörimisnopeus on 50 r/s.
c) Jännitteen huippuarvo on = 3,2 V.
= 3,2 V.
d) Huippuarvon yhtälöstä saadaan magneettivuon tiheyden suuruudeksi
saadaan magneettivuon tiheyden suuruudeksi
 e) Kun silmukka on kiertynyt niin, että sen taso muodostaa 15 asteen kulman magneettikentän suunnan kanssa, silmukan asentoa kuvaavan kulman α suuruus on α = 90°-15° = 75°. Jännitteen hetkellinen arvo, kun silmukan kiertokulma on 75°, on
e) Kun silmukka on kiertynyt niin, että sen taso muodostaa 15 asteen kulman magneettikentän suunnan kanssa, silmukan asentoa kuvaavan kulman α suuruus on α = 90°-15° = 75°. Jännitteen hetkellinen arvo, kun silmukan kiertokulma on 75°, on
%3De_0%5Csin%5Calpha%3D3%7B%2C%7D2V%5Ccdot%5Csin75%C2%B0%5Capprox3%7B%2C%7D1V)
13-6
a) Indusoitunut jännite on e = e0sinc, jossa α on magneettikentän ja silmukan tason normaalin välinen kulma. Silmukan tason ollessa kentän suuntainen kulma α = 90° ja sin90° = 1, jolloin jännite on yhtä suuri kuin huippujännite eli
%5E2%5Ccdot13mT%5Ccdot2%5Cpi%5Ccdot%5Cfrac%7B6600%7D%7B60%7D%5Ccdot%5Cfrac%7B1%7D%7Bs%7D%5Capprox0%7B%2C%7D20V)
b) Kun silmukan taso on magneettikenttää vastaan kohtisuorassa, kulma α = 0° ja sin α = 0. Tällöin magneettivuo silmukan läpi on hetkellisesti nolla ja jännite on nolla.
Induktioliesissä pyörrevirrat kuumentavat suoraan liedelle asetetun metallikattilan pohjaa. Lieden keraaminen pinta johtaa huonosti lämpöä lieden muihin osiin, joten energiaa menee vain vähän hukkaan. Induktiolevyn pinta ei kuumene yhtä paljon kuin metalliset sähkölevyt. Ruokien kuumentaminen induktioliedellä edellyttää metallisten astioiden käyttöä, koska pyörrevirtojen syntyminen edellyttää materiaalilta hyvää sähkönjohtavuutta.
Vaikka teoriassa keittolevyillä olisi mahdollista käyttää myös muita kuin metallisia keittoastioita, lasin ja keramiikan huonon lämmönjohtavuuden ja rikkoutumisvaaran vuoksi kaikki liedelle suunnitellut astiat ovat metallisia, joten induktioliesi ei tässäkään mielessä ole perinteistä lämmön johtumiseen perustuvaa liettä huonompi. Induktioliesien etuja ovat myös nopeus ja hyvä säädettävyys. Induktioliesien energiankulutus on pienempi kuin perinteisten liesien.
13-1
a) i) Silmukan läpi kulkeva magneettivuo on suurin piirroksessa 3. ii) Silmukan läpi kulkeva magneettivuo on pienin piirroksessa 1.
b) i) Lähdejännite on suurin piirroksessa 1. ii) Lähdejännite on pienin (nolla) piirroksessa 3.
13-2
Kohdassa a lähdejännite saavuttaa huippuarvonsa, koska käämin silmukoiden taso on magneettikentän suuntainen (käämin magneettikentän kenttäviivat ovat kohtisuorassa ulkoista magneettikenttää vastaan).
Kohdassa b lähdejännite on nolla, koska käämin silmukoiden taso on kohtisuorassa magneettikenttää vastaan (käämin magneettikentän kenttäviivat ovat samansuuntaiset ulkoisen magneettikentän kanssa).
Kohdassa c lähdejännite kasvaa, joten käämin silmukoiden taso on vinossa magneettikenttää vastaan.
13-5
a) Pyörimisnopeuden kasvattamien lisää vaihtojännitteen taajuutta. Jännitteen suuruuteen vaikuttavat magneettivuon tiheys, käämin pintaala ja kulmanopeus (ja käämin kierrosmäärä, tässä tehtävässä N=1).
b) Koska jaksonaika on 0,020 s = 20 ms, jännitteen taajuus on
c) Jännitteen huippuarvo on
d) Huippuarvon yhtälöstä
13-6
a) Indusoitunut jännite on e = e0sinc, jossa α on magneettikentän ja silmukan tason normaalin välinen kulma. Silmukan tason ollessa kentän suuntainen kulma α = 90° ja sin90° = 1, jolloin jännite on yhtä suuri kuin huippujännite eli
b) Kun silmukan taso on magneettikenttää vastaan kohtisuorassa, kulma α = 0° ja sin α = 0. Tällöin magneettivuo silmukan läpi on hetkellisesti nolla ja jännite on nolla.
11. Induktiolaki
11-6








 Magneettivuo silmukan läpi lopussa
Magneettivuo silmukan läpi lopussa
 Keskimääräinen indukstiojännite on
Keskimääräinen indukstiojännite on
 Keskimääräinen sähkövirta on
Keskimääräinen sähkövirta on

11-1








Magneettivuo silmukan läpi alussa
11-1
a) Epätosi, koska magneettivuon täytyy muuttua
b) Tosi
c) Tosi
d) Tosi
11-4
11-5
a)
b)
11-10
%5Ccdot0%7B%2C%7D010%2752%5Ccdot10%5E%7B-6%7DT%7D%7B20%7B%2C%7D0s%7D%3D23%7B%2C%7D4V%5Capprox23V)
%5E2%7D%3D3%7B%2C%7D05577k%5COmega)

a)
Piikilanka-aitaa voidaan mallintaa yhtenäisellä johdinsilmukalla, johon indusoituvan jännitteen suuruus on
c)
Silmukan resistanssi on
Silmukkaan indusoituvan sähkövirran suuruus on
11-13

%5Ccdot15mT%7D%7B1%7B%2C%7D25s%7D%3D-7%7B%2C%7D5%5Ccdot10%5E%7B-4%7DV) Tällöin johtimessa kulkeva sähkövirta on
Tällöin johtimessa kulkeva sähkövirta on 

%5Ccdot15mT%7D%7B1%7B%2C%7D25s%7D%3D7%7B%2C%7D5%5Ccdot10%5E%7B-4%7DV)

Oletetaan, että hetkellä t=0s silmukan etureuna on kentän reunan kophdalla. Silmukka liikkuu vakionopeudella magneettikentän reunalta kokonaan kenttään ajassa
Muuttuva magneettivuo indusoi silmukkaan jännitteen, joka synnyttää siolmukkaan sähkövirran
Aikavälillä 0,0...1,25s silmukan läpäisevä magneettivuo muuttuu tasaisesti, joten indusoituva keskimääräinen jännite on vakio
Silmukka on kokonaan magneettikentässä ajan
Näin ollen aikavälillä 1,25...3,75s magneettivuo ei muutu, ja siksi indusoitunut jännite on nolla, samoin sähkövirta.
Silmukka poistuu magneettikentästä ajassa 
Aikavälillä 3,75... 5,0 s magneettivuo muuttuu tasaisesti, joten indusoituva keskimääräinen jännite on vakio
Johtimessa kulkevan sähkövirran suuruus on tällöin
Hetkellä 5,0s silmukka poistuu kokonaan magneettikentästä, joten magneettivuo ei muutu, indusoitunut jännite on nolla ja samoin sähkövirta
10. Suoran johtimen induktiolaki
10-1
a) kyllä b) kyllä c) ei (paksuus suunnassa kyllä)
10-4
a) Koska johidin paikkallaan
b) Jännitemittarissa havaitaan välillä positiivinen ja välillä negatiivinen jännite
c) Jänniteen arvo on suurin ,kun johtimeen liikkeen suunta on kohtisuorassa magneettivuon tiheyttä vastaan, tällöin kulma α on 90° ja sinα=1. Jännite on sitä suurempi, mitä nopeammin johdinta liikutetaan. Jännite on likimain nolla, kun johdinta liikutetaan kenttäviivojen suuntaisesti, ja jännite on nolla, jos johdin ei liiku.
d) Jos hyvin kapean silmukan vastakkaiset puolet liikkuvat magneettikentässä, indusoituva jännite on nolla. Tämä johtuu siitä, että johtimen eri osissa elektroneihin kohdistuu yhtä suuret voimat. Eri puolilla silmukkaa magneettiset voimat pyrkivät liikuttamaan elektroneja silmukassa vastakkaisiin suuntiin. Voimien vaikutukset kumoavat toisensa, joten jännite on nolla.
10-6
Vasemman siiven kärjellä on korkeampi potentiaali
10-7











 a)
a)


 eli
eli  . Kun suunta oikealle on valittu positiiviseksi, saadaan skalaariyhtälö
. Kun suunta oikealle on valittu positiiviseksi, saadaan skalaariyhtälö  eli
eli . Näin ollen vetävä voima on yhtä suuri ja vastakkaisuuntainen kuin magneettikentästä sauvaan kohdistuva magneettinen voima. Koska sauva on kohtisuorassa magneettikenttää vastaan, on magneettinen voima suurudeltaan
. Näin ollen vetävä voima on yhtä suuri ja vastakkaisuuntainen kuin magneettikentästä sauvaan kohdistuva magneettinen voima. Koska sauva on kohtisuorassa magneettikenttää vastaan, on magneettinen voima suurudeltaan 
Indusoituva jännite on
10-9
b)
Sauva liikku vakionopeudella, joten Newtonin II lain perusteella
c)
Oikean käden säännön mukaan suunta ylös
9. Sähkömagneettinen induktio
9-1
a) Väite pitää paikkansa.
9-2
9-5
a) Väite pitää paikkansa.
b) Väite on väärä. Käämiin indusoituva jännite aiheutuu käämin läpi menevän magneettivuon muuttumisesta. Käämin läpäisevä magneettivuo voi olla myös vakio, jolloin ei synny induktioilmiötä eikä induktiojännitettä.
c) Väite on väärä. Lenzin lain mukaan induktiovirta on suunnaltaan sellainen, että sen vaikutukset vastustavat induktioilmiön aiheuttaneen magneettikentän muutosta.
d) Väite pitää paikkansa.
9-2
1) Vahvistuva magneettikenttä indusoi silmukkaan sähkövirran, jonka suunta on sellainen, että sen synnyttämä magneettikenttä Lenzin lain mukaan vastustaa magneettikentän kasvua. Sähkövirran aiheuttama kenttä silmukan sisällä on alkuperäiseen kenttään nähden vastakkaissuuntainen. Sähkövirran suunta on oikean käden säännön perusteella silmukan katsojaa lähempänä olevassa osassa ylös.
2) Koska magneettikenttä on heikkenemässä, Lenzin lain mukaan silmukan sisälle syntyy magneettikenttä, joka pyrkii vastustamaan kentän heikkenemistä eli kenttä on vahvistava. Sen suunta on sama kuin alkuperäisen kentän suunta eli kohti katsojaa. Sähkövirran suunta on kuvassa vastapäivään.
b) Magneettivuo on Φ = AB = 28 ∙ 10--4 m2 ∙ 0,14 T ≈ 0,39 mWb
9-5
a) 1) ja 2) Jos käämi otetaan pois magneetin kohtioiden välistä tai käännetään pystyasentoon, käämin läpäisevä magneettivuo pienenee. Vuon pienenemisen aikana käämin napojen välille indusoituu jännite. Tämä havaitaan jännitemittarilla.
b) Käämit on kytketty induktiivisesti, koska niiden sisällä on osittain yhteinen magneettikenttä. Kun käämi 1 kytketään tasajännitteeseen, käämissä 2 havaitaan jännite vain kytkemis- ja katkaisuhetkellä, jolloin magneettivuo käämin läpi muuttuu.
9-6
a) Koska silmukan etäisyys johtimesta pysyy vakiona, silmukan läpäisevä magneettivuo ei muutu eikä silmukkaan indusoidu jännitettä.
b) Koska silmukan etäisyys johtimesta muuttuu, myös silmukan läpäisevä magneettivuo muuttuu ja silmukkaan indusoituu jännite.
c) Koska silmukan etäisyys johtimesta muuttuu, myös silmukan läpäisevä magneettivuo muuttuu ja silmukkaan indusoituu jännite.
d) Koska silmukan etäisyys johtimesta pysyy vakiona, silmukan läpäisevä magneettivuo ei muutu eikä silmukkaan indusoidu jännitettä.
8. Suora johdin ja käämi ulkoisessa magneettikentässä
8-1
a) kenttäviivojen suuntaan
b) kohtisuoraan magneettikenttää vastaan
8-2
a) Ylöspäin
b) Vasemmalle
c) Oikea-alakulmaan
d) Vasemmalle
8-5



 b)
b)




8-6




8-8
Koska johdin pysyy paikallaan ,
, 









 8-9
8-9
a)
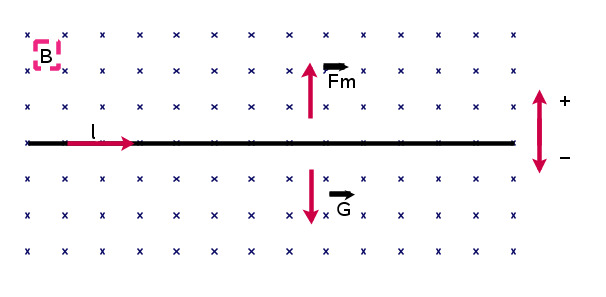
b)





 , jossa
, jossa  on alumiinin tiheys.
on alumiinin tiheys.
%5E2%5Ccdot9%7B%2C%7D81%5Cfrac%7Bm%7D%7Bs%5E2%7D%7D%7B0%7B%2C%7D56T%7D%5Capprox37mA)
 , kun
, kun  on tyhjiön permeabiliteetti,
on tyhjiön permeabiliteetti,  ja
ja  ovat johtimessa kulkevat sähkövirrat, r on johdinten välinen etäisyys ja l virtajohtimien pituus.
ovat johtimessa kulkevat sähkövirrat, r on johdinten välinen etäisyys ja l virtajohtimien pituus.
%7D%7D%7B2%5Cpi%7D%5Ccdot%5Cfrac%7B2%7B%2C%7D5A%5Ccdot2%7B%2C%7D5A%7D%7B0%7B%2C%7D19m%7D%5Ccdot1%7B%2C%7D4m%5Capprox9%7B%2C%7D2%5Ccdot10%5E%7B-6%7DN)
a) kenttäviivojen suuntaan
b) kohtisuoraan magneettikenttää vastaan
8-2
a) Ylöspäin
b) Vasemmalle
c) Oikea-alakulmaan
d) Vasemmalle
8-5
a)
Magneettinen voima  on suurin, kun
on suurin, kun  eli kun α=90. Johdin on siis asetettava kohtisuoraan magneettikenttää vastaan,
eli kun α=90. Johdin on siis asetettava kohtisuoraan magneettikenttää vastaan,
Magneettivuon tiheys on
8-6
Magneettivuon tiheys on
8-8
Koska johdin pysyy paikallaan
johtimeen kohtistuva paino on samakuin magneettikentästä tuleva voima, eli
Paino lasketaan kaavalla
jossa
Koska halutaan saada sähkövirran suuruus,
Koska tehtävässä mainittiin, että johdin on kohtisuorassa kenttäviivojen vastaan,
Johtimen suunta on vasen-oikeasuunnassa, sähkövirran suunta on oikealle
a)

b)
Biotin-Savartin laen mukaan
Koska tässä me halutaan johtimessa kulkevan virran suuruus
Newtonin II lain mukaan on  eli
eli  . Kun suunta ylös valitaan positiiviseksi, skalaariyhtälö on
. Kun suunta ylös valitaan positiiviseksi, skalaariyhtälö on  , joka saadaan muotoon
, joka saadaan muotoon  eli
eli 
 . Johtimen massa voidaan kirjoittaa muotoon
. Johtimen massa voidaan kirjoittaa muotoon
Johdin on muodoltaan suora ympyrälieriö, joten sen tilavuus on
Johtimessa kulkevan sähkövirran suuruus on
8-10
a) Ampèren lain mukaan suora virtajohdin kohdistaa toiseen yhdensuuntaiseen virtajohtimeen voiman, jonka suuruus on
b)
Ksoka virtajohtimissa sähkövirrat kulkevat samaan suuntaan, johtimet vetävät toisiaan puoleensa. Virtajohtimiin kohdistuvat voimat ovat Newtonin III lain mukaan yhtä suuret ja vastakkaissuuntaiset. Voimien suuruudet ovat
7. Varatun hiukkasen liike homogeenisissa sähkö- ja magneettikentässä
7-2
a)
1 Protoni
2 Neutroni
3 Elektroni
b)
i) Protonin rata taipuu ylöspäin
ii) Elekrtonin rata taipuu alaspäin
iii) Neutronin radan suunta pysyy samana
7-4
a)






7-6




 Halutaan saada hiukkasen loppu-nopeus
Halutaan saada hiukkasen loppu-nopeus
![qU=\frac{1}{2}mv_l^2\ <=>v_l=\sqrt[]{\ \frac{2qU}{m}}](https://math-demo.abitti.fi/math.svg?latex=qU%3D%5Cfrac%7B1%7D%7B2%7Dmv_l%5E2%5C%20%3C%3D%3Ev_l%3D%5Csqrt%5B%5D%7B%5C%20%5Cfrac%7B2qU%7D%7Bm%7D%7D)
![v_l=\sqrt[]{\ \frac{2qU}{m}}=\sqrt[]{\frac{2\cdot1{,}602176487\cdot10^{-19}C\cdot150V}{9{,}1093822\cdot10^{-31}kg}}=7263924{,}926\ \frac{m}{s}\approx7{,}3\cdot10^6\ \frac{m}{s}=7{,}3\frac{Mm}{s}](https://math-demo.abitti.fi/math.svg?latex=v_l%3D%5Csqrt%5B%5D%7B%5C%20%5Cfrac%7B2qU%7D%7Bm%7D%7D%3D%5Csqrt%5B%5D%7B%5Cfrac%7B2%5Ccdot1%7B%2C%7D602176487%5Ccdot10%5E%7B-19%7DC%5Ccdot150V%7D%7B9%7B%2C%7D1093822%5Ccdot10%5E%7B-31%7Dkg%7D%7D%3D7263924%7B%2C%7D926%5C%20%5Cfrac%7Bm%7D%7Bs%7D%5Capprox7%7B%2C%7D3%5Ccdot10%5E6%5C%20%5Cfrac%7Bm%7D%7Bs%7D%3D7%7B%2C%7D3%5Cfrac%7BMm%7D%7Bs%7D)
Ja hiukkasen liike-energia saadaan
%5E2%3D2%7B%2C%7D403264783%5Ccdot10%5E%7B-17%7D%5Capprox2%7B%2C%7D4%5Ccdot10%5E%7B-17%7DJ)
7-7
Jotta protonit kulkisivat kenttien läpi suuntansa säilyttäen, liikettä vastaan kohtisuorassa suunnassa on oltava Newtonin II lain mukaan eli
eli  . Valitaan magneettisen voiman suunta positiiviseksi, jolloi skalaariyhtälöstä
. Valitaan magneettisen voiman suunta positiiviseksi, jolloi skalaariyhtälöstä  saadaan
saadaan  eli
eli ja
ja ) (koska on kyseessä homogeeninen sähkökenttä)
(koska on kyseessä homogeeninen sähkökenttä)
)

7-11
a) Elektronisuihkun jokaiseen elektroniin kohdistuvan magneettisen voiman suuruus on
 ja suunta oikean käden säännön perusteella elektronin liikesuuntaan nähden oikealle.
ja suunta oikean käden säännön perusteella elektronin liikesuuntaan nähden oikealle.


7-13


%3D113%7B%2C%7D903u)















 Tinaionien ratojen halkaisijat ovat
Tinaionien ratojen halkaisijat ovat
%5Capprox1%7B%2C%7D15825m)
%5Capprox1%7B%2C%7D16842m)
a)
1 Protoni
2 Neutroni
3 Elektroni
b)
i) Protonin rata taipuu ylöspäin
ii) Elekrtonin rata taipuu alaspäin
iii) Neutronin radan suunta pysyy samana
7-4
a)
Protoniin kohdistuvan mageneettisen voiman suuruus Maan magneettikentässä on
 Protonin kohdistuvan painon suuruus on
Protonin kohdistuvan painon suuruus on
Magneettisen voiman suuruusluokka on  N ja painon
N ja painon  N.
N.
Paino on merkityksetän Maan magneettikentän kohdistamaan voimaan verrattuna: magneettinen voiam on noin 500 miljoonaa kertaa suurempi
b)
7-6
Koska hiukkanen liikkuu homogeenisessä sähökentässä, pätee
Koska hiukkasen alku-nopeus on 0,
Ja hiukkasen liike-energia saadaan
7-7
Jotta protonit kulkisivat kenttien läpi suuntansa säilyttäen, liikettä vastaan kohtisuorassa suunnassa on oltava Newtonin II lain mukaan
levyjen välinen jännite on
7-11
a) Elektronisuihkun jokaiseen elektroniin kohdistuvan magneettisen voiman suuruus on
Huomaa, q on elektronin varauksen itseisarvo
b)
Newtonin II lain mukaan on  , jossa magneettisen voiman suuruus on
, jossa magneettisen voiman suuruus on  ja normaalikiihtyvyyden suuruus
ja normaalikiihtyvyyden suuruus  . Saadaan yhtälö
. Saadaan yhtälö  (q elektronin varauksen itseisarvo), jossa saadaam radam säteeksi
(q elektronin varauksen itseisarvo), jossa saadaam radam säteeksi
c) Elektronin ratanopeus ympyräradalla on vakio. Tällöin on voimassa  . Elektronin kulkema matka sen tehdessä kokonaisen kierroksen on
. Elektronin kulkema matka sen tehdessä kokonaisen kierroksen on  , jossa r on radan säde. Kodan b perusteella
, jossa r on radan säde. Kodan b perusteella  , jossa q on elektronin varauksen itseisarvo.
, jossa q on elektronin varauksen itseisarvo.
Yhteen kierrokseen kulunut aika on
7-13
Tinaionien osumakohtien etäisyys on ionien ratojen halkaisijoiden erotus
Analysoivassa magneettikentässä ionit liikkuvat pitkin ympyrärataa magneetisen voiman vaikutuksesta.
Magneettinen voima on 
Ionit ovat ympyräliikkeessä, jolloin niillä on normaalikiihtyvyyttä
Newtonin II-lain mukaan
Ionit saapuvat analysoivaan magneettikenttään samalal nopeudella, millä ne pääsevät kulkemaan nopeus valitsimen läpi
Nopeus valitsimessa vakionopeudella kulkeville ioneille on
Ionit saapuvat analysoivaan magneettikenttään nopeudella 260 000 m/s.
Ionin radan halkaisija on
Halkaisijoiden erotus on (1,16842-1,15825)m=0,01017m≈10,2mm
V:osumakohtien välinen etäisyys on 10,2mm
6. Magneettikenttä
6-1
6-2
Kun johtimessa kulkee sähkövirta, kompassin neula kääntyy johtimeen nähden. Kompassineula reagoi ulkoiseen magneettikenttään. Kun johtimessa kulkee sähkövirta, johtimen ympärille syntyy magneettikenttä ja tähän kenttään kompassineula reagoi.
6-3
a) a:ssa oikean käden sännön mukaan suunta alas, b:ssä sunta yläs ja c:ssä johtimen suoralla osalla ylös ja lenkissä vastapäiväiseen suuntaan.
b) a:ssa, koska sen kenttäviivat ovat tiheämmässä johtimen a ympärillä kuin johtimen b ympärillä.
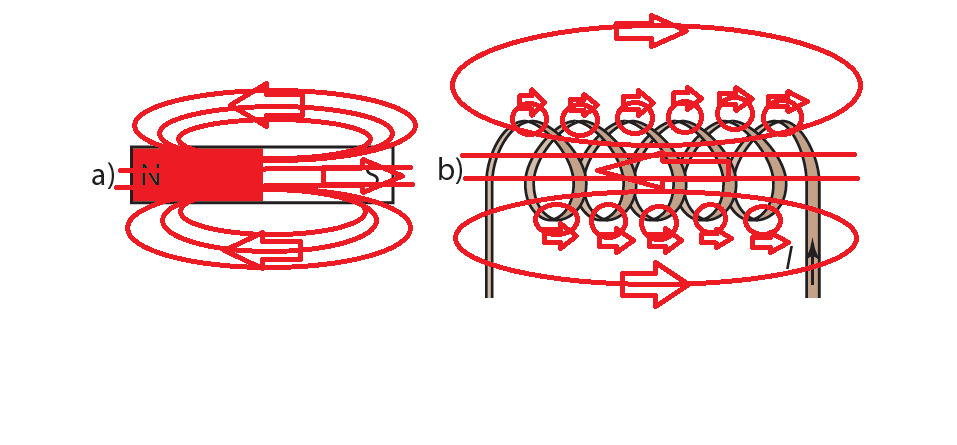
c) Ensimmäisessä tilanteessa kestomagneetin S-kohtio kääntyy kohti käämiä, joten käämin oikeassa päässä on N-kohtio ja vasemmassa S-kohtio. Toisessa tilanteessa kestomagneetin N-kohtio kääntyy kohti käämiä, joten käämin oikeassa päässä on S-kohtio ja vasemmassa N-kohtio.
6-4
a) Magneettivuon tiheys B kuvaa magneettikentän voimakkuutta ja ilmoittaa magneettikentän suunnan, kun taas magneettikenttää vastaan kohtisuoran pinnan läpi kulkevien kenttäviivojen lukumäärää kuvaa magneettivuo.
b) 2
6-5
a) Maapalloa ympäröi magneettikenttä, koska maapallon ytimen uloimpaan, nestemäiseen osaan syntyy pyörimisen ja kuuman kiinteän ytimen vaikutuksesta sähkövirtoja, jotka saavat aikaan magneettikentän.
b) Deklinaatio on magneettineulan poikkeama pohjoissuunnasta. Inklinaatio on magneettineulan kallistuma vaakatasosta. Suomessa deklinaatio on 4-10 astetta itään ja inklinaatio 72-78 astetta. Kuvaan merkitty kulma on inklinaatio. Deklinaatio ja inklinaatio ovat myös tähtitieteessä käytettyjä termejä, jolloin ne eivät liity magnetismiin.
c) Selitys liittyy inklinaatioon. Maan magneettikenttä on vaakasuora vain päiväntasaajalla tai lähellä päiväntasaajaa. Muualla sillä on aina pystysuora komponentti, joka pyrkii vääntämään kompassin neulaa pystyasentoon. Tämä vääntö kumotaan kompassissa neulan painotuksella, jolloin neula asettuu kompassin sisällä likimain vaakasuoraan asentoon. Pohjoisella pallonpuoliskolla toimivissa kompasseissa neulan eteläpää on painavampi ja eteläisellä pallonpuoliskolla toimivissa kompasseissa päinvastoin. Väärän pallonpuoliskon kompassi ei toimi, koska neula on väärässä asennossa eikä pääse liikkumaan vapaasti.
6-7
a) Magneettien välinen vuorovaikutus havaitaan niiden välisen voiman perusteella, samoin sähkövarausten välinen vuorovaikutus havaitaan niiden välisen voiman perusteella. Magneettien samannimiset kohtiot hylkivät toisiaan ja erinimiset kohtiot vetävät toisiaan puoleensa. Vastaavasti saman sähkövarauksen omaavat kappaleet hylkivät toisiaan, eri varauksen omaavat kappaleet vetävät toisiaan puoleensa. Sähkövaraukset voivat olla positiivisia tai negatiivisia: ne voivat esiintyä toisistaan riippumatta ja erillään toisistaan. Sen sijaan magneetin napoja ei voi erottaa toisistaan. Magneetilla on aina sekä pohjoiskohtio ja eteläkohtio. Tämänhetkisen tietämyksen mukaan ei ole olemassa magneettisia monopoleja eli yksinapaisia magneettisia hiukkasia tai kappaleita.
b) Magneettikentän synnyttävät kestomagneetit, sähkömagneetit tai virtajohtimet, joissa kulkee sähkövirta. Sähkövaraukset synnyttävät sähkökentän. Magneettikenttiä havainnollistetaan kenttäviivaesityksillä, joissa kenttäviivojen suunta kertoo kentän suunnan ja tiheys kentän voimakkuutta. Vastaavasti sähkökentän kuvaamiseen käytetään kenttäviivoja. Magneettikentän kenttäviivat ovat sulkeutuvia käyriä, toisin kuin sähkökentän kenttäviivat, ja niitä on sekä magneetin ulko-että sisäpuolella. Magneettikentän voimakkuutta kuvaava suure B on magneettivuon tiheys . Se on vektorisuure kuten sähkökentän voimakkuus E.

6-2
Kun johtimessa kulkee sähkövirta, kompassin neula kääntyy johtimeen nähden. Kompassineula reagoi ulkoiseen magneettikenttään. Kun johtimessa kulkee sähkövirta, johtimen ympärille syntyy magneettikenttä ja tähän kenttään kompassineula reagoi.
6-3
a) a:ssa oikean käden sännön mukaan suunta alas, b:ssä sunta yläs ja c:ssä johtimen suoralla osalla ylös ja lenkissä vastapäiväiseen suuntaan.
b) a:ssa, koska sen kenttäviivat ovat tiheämmässä johtimen a ympärillä kuin johtimen b ympärillä.
c) Ensimmäisessä tilanteessa kestomagneetin S-kohtio kääntyy kohti käämiä, joten käämin oikeassa päässä on N-kohtio ja vasemmassa S-kohtio. Toisessa tilanteessa kestomagneetin N-kohtio kääntyy kohti käämiä, joten käämin oikeassa päässä on S-kohtio ja vasemmassa N-kohtio.
6-4
a) Magneettivuon tiheys B kuvaa magneettikentän voimakkuutta ja ilmoittaa magneettikentän suunnan, kun taas magneettikenttää vastaan kohtisuoran pinnan läpi kulkevien kenttäviivojen lukumäärää kuvaa magneettivuo.
b) 2
6-5
a) Maapalloa ympäröi magneettikenttä, koska maapallon ytimen uloimpaan, nestemäiseen osaan syntyy pyörimisen ja kuuman kiinteän ytimen vaikutuksesta sähkövirtoja, jotka saavat aikaan magneettikentän.
b) Deklinaatio on magneettineulan poikkeama pohjoissuunnasta. Inklinaatio on magneettineulan kallistuma vaakatasosta. Suomessa deklinaatio on 4-10 astetta itään ja inklinaatio 72-78 astetta. Kuvaan merkitty kulma on inklinaatio. Deklinaatio ja inklinaatio ovat myös tähtitieteessä käytettyjä termejä, jolloin ne eivät liity magnetismiin.
c) Selitys liittyy inklinaatioon. Maan magneettikenttä on vaakasuora vain päiväntasaajalla tai lähellä päiväntasaajaa. Muualla sillä on aina pystysuora komponentti, joka pyrkii vääntämään kompassin neulaa pystyasentoon. Tämä vääntö kumotaan kompassissa neulan painotuksella, jolloin neula asettuu kompassin sisällä likimain vaakasuoraan asentoon. Pohjoisella pallonpuoliskolla toimivissa kompasseissa neulan eteläpää on painavampi ja eteläisellä pallonpuoliskolla toimivissa kompasseissa päinvastoin. Väärän pallonpuoliskon kompassi ei toimi, koska neula on väärässä asennossa eikä pääse liikkumaan vapaasti.
6-7
a) Magneettien välinen vuorovaikutus havaitaan niiden välisen voiman perusteella, samoin sähkövarausten välinen vuorovaikutus havaitaan niiden välisen voiman perusteella. Magneettien samannimiset kohtiot hylkivät toisiaan ja erinimiset kohtiot vetävät toisiaan puoleensa. Vastaavasti saman sähkövarauksen omaavat kappaleet hylkivät toisiaan, eri varauksen omaavat kappaleet vetävät toisiaan puoleensa. Sähkövaraukset voivat olla positiivisia tai negatiivisia: ne voivat esiintyä toisistaan riippumatta ja erillään toisistaan. Sen sijaan magneetin napoja ei voi erottaa toisistaan. Magneetilla on aina sekä pohjoiskohtio ja eteläkohtio. Tämänhetkisen tietämyksen mukaan ei ole olemassa magneettisia monopoleja eli yksinapaisia magneettisia hiukkasia tai kappaleita.
b) Magneettikentän synnyttävät kestomagneetit, sähkömagneetit tai virtajohtimet, joissa kulkee sähkövirta. Sähkövaraukset synnyttävät sähkökentän. Magneettikenttiä havainnollistetaan kenttäviivaesityksillä, joissa kenttäviivojen suunta kertoo kentän suunnan ja tiheys kentän voimakkuutta. Vastaavasti sähkökentän kuvaamiseen käytetään kenttäviivoja. Magneettikentän kenttäviivat ovat sulkeutuvia käyriä, toisin kuin sähkökentän kenttäviivat, ja niitä on sekä magneetin ulko-että sisäpuolella. Magneettikentän voimakkuutta kuvaava suure B on magneettivuon tiheys . Se on vektorisuure kuten sähkökentän voimakkuus E.
