Tehtävät

2.1

202

$\int_{ }^{ }3\cdot\left(3x-1\right)^5dx=\frac{1}{6}\left(3x-1\right)^6+C$

$\int_{ }^{ }6x\left(3x^2-5\right)^4dx=\frac{1}{5}\left(3x^2-5\right)^5+C$

203

$\int_{ }^{ }15\left(3x+2\right)^3dx=\frac{5}{4}\left(3x+2\right)^4+C$

$\int_{ }^{ }\left(4x-6\right)^4dx=\frac{1}{20}\left(4x-6\right)^5+C$

204

$\int_{ }^{ }6x^2\left(x^3+3\right)^6dx=2\int_{ }^{ }3x^2\left(x^3+3\right)^6=\frac{2}{7}\left(x^3+3\right)^7+C$

b)
$\int_{ }^{ }\left(\frac{x}{3}+1\right)^5dx=\frac{1}{2}\left(\frac{x}{3}+1\right)^6+C$

5.2

534

Poikkileikkauksen pinta-ala: $A\left(x\right)=y^2=\left(2\cdot4{,}25e^{2{,}67-0{,}889x}\right)^2$

Tilavuus välillä

$0\le x\le300$

$V=\int_0^{300}\left(2\cdot4{,}25e^{^{2{,}67-0{,}0089x}}\right)^2dx=842\ 292m^3$

Tilavuus olisi n.840 000m³.

535

a) Poikkileikkausneliön sivun pituus kohdassa x on x²

b) Poikkileikkausneliön pinta-ala on $A\left(x\right)=x^2\cdot x^2=x^4$

c) Kappaleen tilavuus on

$\int_0^1x^4dx=\bigg/_{\!\!\!\!\!0}^1\frac{1}{5}x^5=\frac{1}{5}$

537

a) Korkeus on molemmissa kappaleissa sama, 2.

Kappale A: Poikkileikkaukset ovat ympyröitä, joiden halkaisija kohdassa x on $\frac{2}{x}$

Kappale B: Poikkileikkaukset ovat ympyröitä, joiden halkaisija x on $2\cdot\frac{1}{x}=\frac{2}{x}$ .

Koska molempien poikkileikkausympyröiden halkaisijat ovat samat, ovat myös pinta-alat samat ja siten myös kappaleiden tilavuudet ovat samat.

b) Tilavuus on

$V\left(x\right)=\pi\int_1^3\left(\frac{1}{x}\right)^2dx=\frac{2\pi}{3}$ (Laskin)

5.1

504

Tilavuus
$V=\pi\int_1^5\left(\sqrt[]{x-1}\right)^2dx=8\pi$ (Laskin)

$V=\pi\int_1^4\left(x-2\right)^2dx=\pi\int_1^4\left(x^2-4x+4\right)dx=\pi\bigg/_{\!\!\!\!\!1}^4\left(\frac{1}{3}x^3-2x^2+4x\right)=3\pi$

502

$V=2\cdot\pi\int_0^2f\left(x\right)^2dx=2\pi\ \int_0^2x^2dx=2\pi\bigg/_{\!\!\!\!\!0}^2\frac{1}{3}x^3=2\pi\left(\frac{1}{3}2^3-\frac{1}{3}0^3\right)=\frac{16\pi}{3}$

b)
$V=\pi\int_{-1}^2f\left(x\right)^2dx=\pi\int_{-1}^2\left(\frac{1}{2}x^3\right)^2dx=\pi\int_{-1}^2\frac{1}{4}x^6dx=\pi\bigg/_{\!\!\!\!\!{-1}}^2\frac{1}{28}x^7=\pi\cdot\left(\frac{1}{28}\cdot2^7-\frac{1}{28}\cdot\left(-1\right)^7\right)=\frac{129}{28}\pi$

503

$V=\pi\int_1^3f\left(x\right)^2dx=\pi\int_1^3\left(\frac{1}{x}\right)^2dx=\pi\int_1^3x^{-2}dx=\pi\bigg/_{\!\!\!\!\!1}^3-\frac{1}{x}=\pi\left(-\frac{1}{3}-\left(-1\right)\right)=\frac{2\pi}{3}$

$V=\pi\ \int_1^2f\left(x\right)^2dx=\pi\int_1^2\left(\frac{1}{\sqrt[]{x}}\right)^2dx=\pi\int_1^2\left(x^{-\frac{1}{2}}\right)^2=\pi\int_1^2x^{-1}dx=\pi\bigg/_{\!\!\!\!\!1}^2\ln x=\pi\left(\ln2-\ln1\right)=\pi\ln2$

505

$V=\int_0^1\pi\left(e^x-2\right)^2dx=\pi\int_0^1\left(e^{2x}-4e^x+4\right)dx=\frac{\pi}{2}\left(e^2-8e+15\right)$

508

Lasketaan funktioiden leikkauspisteet

$x+1=\left(x-1\right)^2$

$x+1=x^2-2x+1$
$x=x^2-2x$
$x^2-3x=0$
$x=0\ tai\ x=3$ (Laskin)

Lasketaan rajattu alueen pinta-ala välillä [0,3]

$\pi\int_0^3\left(x^2-3x\right)^2dx=\frac{72\pi}{5}$ (Laskin)

509

Lasketaan funktioiden leikkauspisteet

$\frac{1}{4}x^2+2=\frac{1}{2}x^2+1$

$x=-2\ tai\ x=2$

Lasketaan pyörähdyskappaleen tilavuus välillä [-2,2]

$V=\pi\int_{-2}^2\left(\frac{1}{4}x^2+2\right)^2dx-\pi\int_{-2}^2\left(\frac{1}{2}x^2+1\right)^2dx=\frac{48\pi}{5}$

510

Käyrien $y_1=e^{\frac{x}{2}}$ ja $y_2=e^{-\frac{x}{2}}$ leikkauskohdat

$e^{\frac{x}{2}}=e^{-\frac{x}{2}}$

$\frac{x}{2}=-\frac{x}{2}$

$x=-x$
$x=0$

Lasketaan kappaleen tilaavus välillä [0,1]

$\pi\int_0^1\left(y_1\right)^2dx-\pi\int_0^1\left(y_2\right)^2dx=\pi\left(e-1\right)-\left(-\pi\left(\frac{1}{e}-1\right)\right)=\pi\left(e+\frac{1}{e}-2\right)$

Käyrät eivät leikkaa, koska yhtälöllä $\sqrt[]{x}=\sqrt[]{x+1}$ ei ole ratkaisuja

Käyrän $y=\sqrt[]{x}$ nollakohta on x=0 ja käyrän $y=\sqrt[]{x+1}$ nollakohta on x=-1

Koska välillä [−1, 1] olevassa testipisteessä x=0,

$\sqrt[]{0+1}=1>\sqrt[]{0}=0$ , on käyrä $y=\sqrt[]{x+1}$ ylempänä kuin käyrä $y=\sqrt[]{x}$ .

Käyrä $y=\sqrt[]{x}$ pyörähtää välillä [0,1] ja käyrä $y=\sqrt[]{x+1}$ välillä [-1,1]

$V_1=\pi\int_{-1}^1\left(\sqrt[]{x+1}\right)^2dx=2\pi$ (Laskin)

$V_2=\pi\int_0^1\left(\sqrt[]{x}\right)^2dx=\frac{1}{2}\pi$ (Laskin)

Kysytyn pyörähdyskappaleen tilavuus on

$V=V_1-V_2=\frac{3\pi}{2}$

512

Muutetaan ellipsin yhtälö $x^2+1{,}7y^2=100$ muotoon $y=f\left(x\right)$

$x^2+1{,}7y^2=100$
$1{,}7y^2=100-x^2$
$y=f\left(x\right)=\sqrt[]{\frac{100-x^2}{1{,}7}}$

$V=\pi\int_{-10}^{10}\left(\sqrt[]{\frac{100-x^2}{1{,}7}}\right)^2dx=\pi\int_{-10}^{10}\frac{100-x^2}{1{,}7}dx=2463.9942...cm^3\approx2500cm^3=2{,}5l$

Tulos on järkevä, sillä se on hieman vähemmän kuin 2640cm³

Emmä jaksa

513
a)
Pyörähdyskappaleen tilavuus ratkaistaan integroimalla muuttujan y suhteen.

$V=\pi\int_1^2\left(2y\right)^2dy=\frac{28}{3}\pi$
b)

Pyörähdyskappaleen tilavuus ratkaistaan
integroimalla muuttujan y suhteen.
Ratkaistaan käyrän yhtälö muuttujan x
suhteen.

$y=\sqrt[]{x}$

$x=y^2$

$V=\pi\int_0^2\left(y^2\right)^2dy=\frac{32\pi}{5}$ (Laskin)

514

a)Lasketaan kahvimukin vetoisuus eli sisätilavus.

Sisätilavuus saadaan, kun sisempi suora y=6x-18 pyörähtää y-akselin ympäri

Ratkaistaan suoran yhtälöstä x

$y=6x-18$

$6x=y+18$
$x=\frac{1}{6}y+3$

Mukin pohjan paksuus on 1,0cm, joten integroimisväli on [1,11]

$V_{sisä}=\pi\int_1^{11}\left(\frac{1}{6}y+3\right)^{^2}dy=\frac{8765\pi}{54}\approx509{,}927\ \left(Laskin\right)$

Kahvin vetoisuus on 509,927cm³=0,509927dm³=

Lasketaan ulkotilavuus

Ulkotilavuus saadaan, kun ulompi suora y=6x-20 pyörähtää y-akselin ympäri

Ratkaistaan suoran yhtälöstä x

$y=6x-20$

$x=\frac{1}{6}y+\frac{10}{3}$

$V_{ulko}=\pi\int_0^{11}\left(\frac{1}{6}y+\frac{10}{3}\right)^2dy=\frac{21791}{108}\pi\approx633{,}874\left(Laskin\right)$

Posliinin määrä saadaan tilavuuksien erotuksena.

$V_{ulko}-V_{sisä}=\frac{21791\pi}{108}-\frac{8765\pi}{54}=\frac{4261\pi}{108}\approx123{,}947$

Posliinin määrä on n.120cm³

516

Kappaleen ulompi osa on ”kiekko”, joka syntyy, kun suora x = 5 pyörähtää y-akselin ympäri ja sisempi osa on ”malja”, joka syntyy, kun käyrä $y=\sqrt[]{3x-6}$ pyörähtää y-akselin ympäri

Sisempi osa:

Ratkaistaan yhtälöstä $y=\sqrt[]{3x-6}$ muuttuja x:

$y=\sqrt[]{3x-6}$

$y^2=3x-6$ , josta $x=\frac{y^2+6}{3}$

Integroinin yläraja, kun x=5

$y=\sqrt[]{3\cdot5-6}=\sqrt[]{9}=3$

Sisemmän pyörähdyskappaleen tilavuus on

$V_{sisempi}=\pi\int_0^3\left(\frac{y^2+6}{3}\right)^2dy=\frac{147\pi}{5}$ (Laskin)

Ulompi pyörähdyskappale on suora lieriö, jonka pohjan säde on 5 ja korkeus on 3.

$V_{ulompi}=\pi\cdot5^2\cdot3=75\pi$

Koko kappaleen tilavuus

$V_{ulompi}-V_{sisempi}-75\pi-\frac{147\pi}{5}-\frac{228\pi}{5}$

517

Lasketaan funktio $y=\sqrt[]{2x-1}$ nollakohdat

$\sqrt[]{2x-1}=0$

$2x-1=0$
$2x=1$
$x=\frac{1}{2}$

Eli funktion ylä-raja alkaa pisteestä x=1/2 ja ala-raja on jokin piste a

$V=\pi\int_{\frac{1}{2}}^a\left(\sqrt[]{2x-1}\right)^2dx=\frac{\left(4a^2-4a+1\right)\cdot\pi}{4}$ (Laskin)

Ratkaistaan yhtälö

$V=4\pi$

$\frac{\left(4a^2-4a+1\right)\cdot\pi}{4}=4\pi\ \ \ \ \ \left|\right|:\pi$

$a=-\frac{3}{2\ }\ tai\ a=\frac{5}{2}$

518
Lasketaan ensin ulomman kappaleen tilavuus, joka syntyy kun suora y=4 pyörähtää x-akselin ympäri ja sitten sisemmän kappaleen tilavuus, joka syntyy kun paraabeli $x=1+y^2$ pyörähtää x-akselin ympäri.

Ratkaistaan yhtälö muuttujan y suhteen

$x=1+y^2$

$y^2=x-1$
$y=\pm\sqrt[]{x-1}$

Voidaan valita pyörähtäväks käyräksi

$y=\sqrt[]{x-1}$

Käyrän $y=4$ ja $y=\sqrt[]{x-1}$ leikkauskohta on

$4=\sqrt[]{x-1}$

$x-1=16$
$x=17$

Käyrän $y=\sqrt[]{x-1}$ ja x-akselin leikkauskohta on x=1

Tilavuus saadaan pyörähdyskappaleiden tilavuutena käyristä y=4 välillä [1,17]

$V_{ulompi}=\pi\int_0^{17}4^2dx=272\pi$ (Laskin)

$V_{sisempi}=\pi\int_1^{17}\sqrt[]{x-1}dx=128\pi$ (Laskin)

$V_{ulompi}-V_{sisempi}=289\pi-128\pi=144\pi\approx452{,}389$

$452{,}389cm^3=0{,}452389dm^3=0{,}000452389m^3$

Lasketaan maljakon massa m tiheyden ρ avulla

$\rho=\frac{m}{V}{,}\ josta\ m=\rho V$

$m=3600\ \frac{kg}{m^3}\cdot0{,}000452389m^3=1{,}6286kg\approx1{,}6kg$

Maljakon massa on 1,6 kg

520
Tangentin kulmakerroin:

$D\frac{1}{x}=Dx^{-1}=-x^{-2}=-\frac{1}{x^2}$

Kulmakertoimen arvo, kun x=1.

$k=-\frac{1}{1^2}=-1$ Tangentti kulkee pisteen (1,1) kautta

Tangentin yhtälö on y-1=-(x-1), josta y=-x+1

Pyörähtävä alue jää käyrän y=1/x ja y=-x+2 väliin välillä [1,2]

Kappaleen tilavuus saadaan kun ulomman käyrän y=1/x pyörähtäessä syntyvästä kappaleesta vähennetään tangentin y=−x + 2 pyörähtäessä syntyvän kappaleen tilavuus. Pyörähdyskappaleen tilavuus:

$V_{ulompi}=\pi\int_1^2\left(\frac{1}{x}\right)^2dx=\frac{1}{2}\pi$ (Laskin)

$V_{sisempi}=\pi\int_1^2\left(-x+2\right)^2dx=\frac{1}{3}\pi$ (Laskin)

$V_{ulompi}-V_{sisempi}=\frac{1}{2}\pi-\frac{1}{3}\pi=\frac{1}{6}\pi=\frac{\pi}{6}$

Kappaleen tilavuus on π/6

524
Käyrän $y=e^x$ pyörähtäminen suoran y=c ympäri on sama tilanne, kuin jos käyrä $y=e^x-c$ pyörähtäisi x-akselin ympäri

Määritetään pyörähdyskappaleen tilavuus välillä [-1,1]

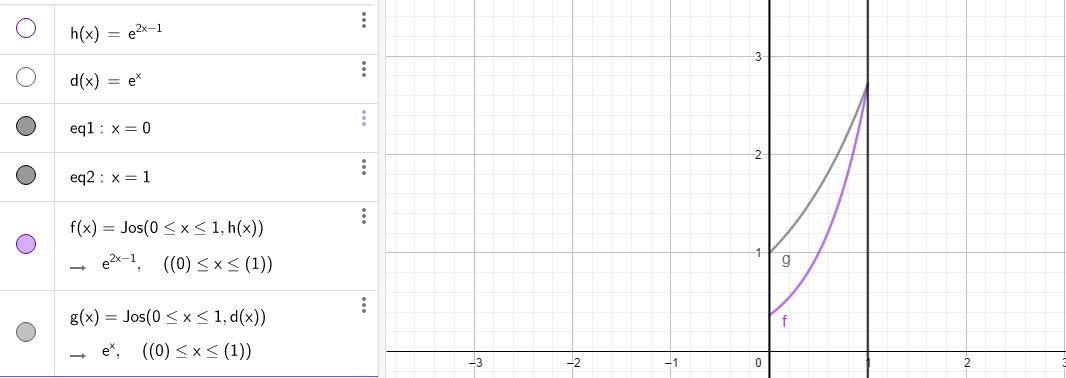
$\pi\int_{-1}^1\left(e^x-c\right)^2=\pi\int_{-1}^1\left(e^{2x}-2ce^x+c^2\right)dx=V\left(c\right)$

Tilavuusfunktio on muuttujan c toisen asteen funktio. Sen kuvaaja on ylöspäin aukeava paraabeli, jonka pienin arvo saavutetaan huipussa. Huippu on derivaatan nollakohdassa

$D\left(\pi\left(2c^2-\left(2e-\frac{2}{e}\right)c-\frac{1}{2e^2}+\frac{1}{2}e^2\right)\right)=\pi\left(4c-2e+\frac{2}{e}\right)$

$\pi\left(4c-2e+\frac{2}{e}\right)=0$

$c=\frac{e}{2}-\frac{1}{2e}=\frac{e^2-1}{2e}$

Vakion c tulee olla $\frac{e^2-1}{2e}$ , jotta tilavuus olisi pienin

4.2

431

$x^2+2x-5=7-x^2$
$x=-3\ tai\ x=2$

Otetaan testipisteeksi välin keskiarvo $-\frac{1}{2}$

$f\left(x\right)=x^2+2x-5-7$

$g\left(x\right)=7-x^2$

$f\left(-\frac{1}{2}\right)=-\frac{23}{4}$ (Laskin)

$g\left(-\frac{1}{2}\right)=\frac{27}{4}$ (Laskin)

Laskujen perusteella funktio g(x) on ylempänä, koska sen arvo pisteessä $x=-\frac{1}{2}$ on suurempi

$A=\int_{-3}^2\left(f\left(x\right)-g\left(x\right)\right)=\frac{125}{3}=41\frac{2}{3}$

432

$x^3-x^2-x=x$

$x=−1\ tai\ x=0\ tai\ x=2$ (laskin)

f(x) on ylempänä välillä ]-1,0[, ja g(x) on ylempänä välillä ]0,2[

$A_1=\int_{-1}^0\left(f\left(x\right)-g\left(x\right)\right)=\frac{5}{12}$
$A_2=\int_0^2\left(g\left(x\right)-f\left(x\right)\right)=\frac{8}{3}$
$A_{kok}=\frac{5}{12}+\frac{8}{3}=\frac{37}{12}=3\frac{1}{12}$

433

$A_1=\int_{-3}^1f\left(x\right)-g\left(x\right)dx=10-2=8$

$A=\int_1^7f\left(x\right)-g\left(x\right)=23-\left(-5\right)=28$

$A=28+8=36$

434

Lasketaan funktioiden leikkauspisteet

$x+6=x^2$

$-x^2+x+6=0$

$x=\frac{-1\pm\sqrt[]{1^2-4\cdot\left(-1\right)\cdot6}}{2\cdot\left(-1\right)}=\frac{-1\pm5}{-2}$
$x=\frac{-1+5}{-2}=-2\ tai\ x=\frac{-1-5}{-2}=3$

$\int_{-2}^3\left(-x^2+x+6\right)dx=\bigg/_{\!\!\!\!\!{-2}}^3-\frac{1}{3}x^3+\frac{1}{2}x^2+6x=\left(-\frac{1}{3}\cdot3^3+\frac{1}{2}\cdot3^2+6\cdot3\right)-\left(-\frac{1}{3}\cdot\left(-2\right)^3+\frac{1}{2}\cdot\left(-2\right)^2+6\left(-2\right)\right)=\frac{125}{6}=20\frac{5}{6}$

Suoran nollakohta on

$x+6=0$

$x=-6$

Lasketaan suora, y-akseli ja x-akseli rajaaman alueen pinta-ala

$A_a=\frac{6\cdot6}{2}=18$

Lasketaan paraapelin ja suoran rajaaman alueen pinta-ala välillä [-2,0]

$A_b=\int_{-2}^0\left(-x^2+x+6\right)dx=\bigg/_{\!\!\!\!\!{-2}}^0-\frac{1}{3}x^3+\frac{1}{2}x^2+6x=\left(-\frac{1}{3}\cdot0^3+\frac{1}{2}\cdot0^2+6\cdot0\right)-\left(-\frac{1}{3}\cdot\left(-2\right)^3+\frac{1}{2}\cdot\left(-2\right)^2+6\cdot\left(-2\right)\right)=7\frac{1}{3}$

$A_2=A_a-A_b=10\frac{2}{3}$

436

Lasketaan funktioiden leikkauspisteet

$e^x=e^{2x-1}$

$e^x-e^{2x-1}=0$
$x=1$

Lasketan funktioiden rajaama alueen pinta-ala välillä [0,1]

$\int_0^1\left(e^x-e^{2x-1}\right)dx=\frac{\left(e^2-2e+1\right)\cdot e^{-1}}{2}$

438

Leikkauskohdat

$\sin x=\cos x$

$\frac{\sin x}{\cos x}=1$
$\tan x=1$
$x=\frac{\pi}{4}+n\cdot\pi$

Leikkauskohdista välillä 0≤x≤π/2 on x=π/4

Alue koostuu kahdesta osasta. Välillä [0,π/4] käyrän sinx ja x-akselin rajaamasta osasta ja välillä [π/4,π/2] käyrän cosx ja x-akselin rajaamasta osasta

Käyrien rajoittaman alueen pinta-ala on

$\int_0^{\frac{\pi}{4}}\left(\sin x\right)dx+\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\left(\cos x\right)dx=\bigg/_{\!\!\!\!\!0}^{\frac{\pi}{4}}\left(-\cos x\right)+\bigg/_{\!\!\!\!\!{\frac{\pi}{4}}}^{\frac{\pi}{2}}\left(\sin x\right)$
$=\left(-\cos\frac{\pi}{4}+\cos0\right)+\left(\sin\frac{\pi}{2}-\sin\frac{\pi}{4}\right)$
$=\left(-\frac{1}{\sqrt[]{2}}+1\right)+\left(1-\frac{1}{\sqrt[]{2}}\right)$
$=2-\sqrt[]{2}$

Käyrien ja y-akselin väliin jäävä alue on käyrien y=sinx ja y=cosx väliin välillä [0,π/4] jäävä alue

Käyrien väliin jäävä pinta-ala on

$A=\int_0^{\frac{\pi}{4}}\left(\cos x-\sin x\right)dx=\bigg/_{\!\!\!\!\!0}^{\frac{\pi}{4}}\left(\sin x+\cos x\right)$

$=\left(\sin\frac{\pi}{4}+\cos\frac{\pi}{4}\right)-\left(\sin0+\cos0\right)$
$=\left(\frac{1}{\sqrt[]{2}}+\frac{1}{\sqrt[]{2}}\right)-\left(0+1\right)=\frac{^{\left(\sqrt[]{2}\right)}2}{\sqrt[]{2}}-1=\frac{2\sqrt[]{2}}{2}-1=\sqrt[]{2}-1$

443

$\int_{-1}^1\left(\left(-x^2+1\right)-\left(x+b\right)\right)dx=\bigg/_{\!\!\!\!\!{-1}}^1\left(\left(-\frac{1}{3}x^3+x\right)-\left(\frac{1}{2}x^2+bx\right)\right)=\bigg/_{\!\!\!\!\!{-1}}^1\left(-\frac{1}{3}x^3-\frac{1}{2}x^2+x-bx\right)$

$A=\left(-\frac{1}{3}-\frac{1}{2}+1-b\right)-\left(\frac{1}{3}-\frac{1}{2}-1+b\right)=\frac{4}{3}-2b$

$\frac{4}{3}-2b=8$

$-2b=\frac{20}{3}\ \ \ \ \ \left|\right|:\left(-2\right)$
$b=-\frac{10}{3}=-3\frac{1}{3}$

4.1

401

$f\left(x\right)=x^2-1$

$A=-\int_{-1}^1f\left(x\right)dx=-\bigg/_{\!\!\!\!\!{-1}}^1\left(\frac{1}{3}x^3-x\right)$

$A=-\left(f\left(1\right)-f\left(-1\right)\right)=-\left(\frac{1}{3}-1-\left(-\frac{1}{3}\right)-1\right)=-\left(-\frac{4}{3}\right)=\frac{4}{3}$
b)

$f\left(x\right)=x^3-2x^2$

$A=-\int_0^2\left(x^3-2x^2\right)=-\bigg/_{\!\!\!\!\!0}^2\left(\frac{1}{4}x^4-\frac{2}{3}x^3\right)$

$A=-\left(\frac{1}{4}\cdot2^4-\frac{2}{3}\cdot2^3-0\right)=-\left(-\frac{4}{3}\right)=\frac{4}{3}$

403

$f\left(x\right)=x^2-4x-5$

$x=5$ tai $x=-1$ (Laskin)

$f\left(2\right)=2^2-8-5=-9$

Pinta-alaa rajaa y-akseli, joten väli on x=0

Pinta-alaa rajaa suora x=1, joten kysytty pinta-ala on välillä [0,1]

Edellisessä tehtävässä lasketun nollakohdan puolivälin arvo on negatiivinen, joiten rajattu alue on myös negatiivinen(ylöspäin aukeava)

Tällöin

$A=-\int_0^1f\left(x\right)dx=-\bigg/_{\!\!\!\!\!0}^1\left(\frac{1}{3}x^3-2x^2-5x\right)$

$A=-\left(\frac{1}{3}\cdot1^3-2\cdot1^2-5\cdot1-0\right)=-\left(-\frac{20}{3}\right)=\frac{20}{3}=6\frac{2}{3}$

404

$\int_0^{2\pi}f\left(x\right)dx=\bigg/_{\!\!\!\!\!0}^{2\pi}\left(-\cos x\right)$

$=-1-\left(-1\right)=0$

Tehtävässä halutaan laskea pinta-alaa välillä [0,2π]

Merkkikaavion perusteella voidaan oleta, että funktio välillä [0,π] on positiivinen, ja [π,2π] negatiivinen

$A=\int_0^{\ 2\pi}\left|\sin x\right|dx=4$ (laskin)

407

Suora 2x+y-8=0 on ratkaistussa muodossa y=-2x+8. Paraabeli y=x²

Lasketaan ensi funktioiden leikkauspisteet

$-2x+8=x^2\ \ \ \ \$

$-x^2-2x+8=0$
$x=−4$ tai $x=2$

Ja seuraavaksi funktioiden nollakohdat

$-2x+8=0$
$-2x=-8\ \ \ \ \ \left|\right|:\left(-2\right)$
$x=4$

$x^2=0$
$x=0$

Koska väli on positiivisella puolella, leikkauspiste pisteessä x=-4 ei huomioitaan.

Eli halutaan saada suora -2x+8 ja paraabelin x² pinta-ala välillä [0,4]

Tätä väliä voidaan jakaa kahteen eri osaa: [0,2] ja [2,4]

Lasketaan paraapelin avulla välin [0,2] pinta-ala ja suoran avulla pinta-ala välillä [2,4]

$A_1=\int_0^2f\left(x\right)dx=\bigg/_{\!\!\!\!\!0}^2\left(\frac{1}{3}x^3\right)$

$A_1=\left(\frac{1}{3}2^3-0\right)=\frac{8}{3}$

$A_2=\int_2^4\left(-2x+8\right)dx=\bigg/_{\!\!\!\!\!2}^4\left(-x^2+8x\right)$
$A_2=\left(\left(-4^2+8\cdot4\right)-\left(-2^2+8\cdot2\right)\right)=\left(16-12\right)=4$
$A_{kok}=\frac{8}{3}+4=\frac{20}{3}=6\frac{2}{3}$

408

a) $-3$
b) $\frac{5}{2}$
c) $\frac{5}{2}+\left(-3\right)=-\frac{1}{2}$

d) $-\frac{2}{3}$
e)

409

Käyrä muodostaa akselien kanssa alueen, joten ensimmäinen aluetta rajaava suora on kohdassa x=0

Toisen suoran saadaan laskemalla käyrän nollakohdat

$e^x-2=0$

$e^x=2$
$\log_e2=x$
$x=\ln2$

Koska aro kohdassa x=ln2 on 0, tarvitaan kohdan x=0 arvo

$e^0-2=1-2=-1$

Koska arvo on negatiivinen, janojen rajaama alue on negatiivinen

Halutaan laskea se alue joka on välillä [0,ln2]

$A=-\int_0^{\ln2}\left(e^x-2\right)dx=-\bigg/_{\!\!\!\!\!0}^{\ln2}\left(e^x-2x\right)$

$A=-\left(e^{\ln2}-2\cdot\left(\ln2\right)-e^0-2\cdot0\right)=\left(2-2\ln2-1\right)=2\ln2-1$

Aluetta rajaa suorat x=3, x-akseli ja funktio f(x)

Aluetta rajaava suora on funktio f(x) ja x-akseli leikkauspisteellä

Lasketaan funktion nollakohdat

$\frac{1}{x}-1=0$
$\frac{1}{x}=1$

$x=1$

Koska aro kohdassa x=1 on 0, tarvitaan kohdan x=3 arvo
$\frac{1}{3}-1=-\frac{2}{3}$
Arvo on negatiivinen, janojen rajaama alue on negatiivinen
Halutaan laskea se alue joka on välillä [1,3]
$A=-\int_1^3\left(\frac{1}{x}-1\right)dx=-\bigg/_{\!\!\!\!\!1}^3\left(\ln\left|x\right|-x\right)$
$A=-\left(\ln3-3-\left(-1\right)\right)=-\left(\ln3-2\right)=2-\ln3$

410

Lasketaan funktion f(x) nollakohdat

$\sqrt[]{3-x}=0$

$3-x=0$
$-x=-3$
$x=3$

Lasketaan suoran y nollakohta

$x+3=0$
$x=-3$

Lasketaan funktioiden leikkaupisteet

$\sqrt[]{3-x}=x+3$

$x=-1$ (laskin)

Koska suora on nouseva, ja funktiolla f(x) on vain ratkaisuja kun x≤0, joten alue on positiivinen

Alueet ovat välillä [-3,-1] ja [-1,3]

$A_1=\int_{-3}^{-1}\left(x+3\right)dx=\bigg/_{\!\!\!\!\!{-3}}^{-1}\left(\frac{1}{2}x^2+3x\right)$

$A_1=f\left(-1\right)-f\left(-3\right)=2$
$A_2=\int_{-1}^3\left(\sqrt[]{3-x}\right)dx=\int_{-1}^3\left(\left(3-x\ \right)^{\frac{1}{2}}\right)dx=\bigg/_{\!\!\!\!\!{-1}}^3\left(\frac{-2\left(3-x\right)^{\frac{3}{2}}}{3}\right)$
$A_2=f\left(3\right)-f\left(-1\right)=\frac{16}{3}$

$A_{kok}=2+\frac{16}{3}=\frac{22}{3}=7\frac{1}{3}$

413

Lasketaan suorakulmion pinta-ala
$A_s=2\cdot1=2$
Käyrän nollakohdat välillä [-1,1] on
$\cos2x=0{,}\ \left[-1{,}1\right]$
$x=\frac{\pi}{4}\ ja\ x=-\frac{\pi}{4}$ (laskin)

Käyrän pinta-ala välillä [ $-\frac{\pi}{4}{,}\ \frac{\pi}{4}$ ]

$A=\int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}\left(\cos2x\right)dx=1$

$\frac{2}{2}=1$

Joten käyrän yläpuolella on suorakulmiosta yhtä paljo kuin alapuolella.

416
a)

1,5 tai -1,5

Koska käyrän pinta-ala voi olla 2 kun se on joko ylöspäin tai alaspäin aukeava

joten sen pinta-ala funktio voi olla joko

$\int_{-1}^1\left(ax^2-a\right)dx=\bigg/_{\!\!\!\!\!{-1}}^1\frac{a}{2+1}x^{2+1}-ax=\bigg/_{\!\!\!\!\!{-1}}^1\frac{a}{3}x^3-ax$

tai

$-\int_{-1}^1\left(ax^2-a\right)dx=-\bigg/_{\!\!\!\!\!{-1}}^1\frac{a}{2+1}x^{2+1}-ax=-\bigg/_{\!\!\!\!\!{-1}}^1\frac{a}{3}x^3-ax$

Tällöin a voi olla

$A=f\left(1\right)-f\left(-1\right)=2$

$a=-1{,}5$

tai

$A=-\left(f\left(1\right)-f\left(-1\right)\right)=2$
$a=1{,}5$

420

Käänetään oikealle avautuva paraapeli x-akselin suuntaan

Tällöin sen funktio on

$y=f\left(x\right)=x^2+x-2$

Lasketaan paraabelin nollakohdat x-akselilla

$x^2+x-2=0$

$x=-2\ tai\ x=1$ (Laskin)

Koska paraapeli on ylöspäin aukeava, ja sillä on nollakohdat

Tällöin rajattu alue on x-akselin alapuolella eli on lisättävä integraalifuntion eteen ''-'' merkki

Lasketaan paraapelin ja x-akselin rajoittaman alueen pinta-ala välillä [-2,1]

$-\int_{-2}^1\left(x^2+x-2\right)dx=\bigg/_{\!\!\!\!\!{-2}}^1\left(\frac{1}{3}x^3+x^2-2x\right)$

$A=-\bigg/_{\!\!\!\!\!{-2}}^1\left(\frac{1}{3}x^3+x^2-2x\right)=\frac{9}{2}=4\frac{1}{2}$

3.2

319

a) C

b) A

c) B

320

$\int_1^3\left(6x-x\right)^2dx=\int_1^3\left(5x\right)^2dx=\int_1^325x^2dx=25\cdot\int_1^3x^2=25\cdot\bigg/_{\!\!\!\!\!1}^3\frac{1}{3}x^3=\frac{25x^3}{3}$

$f\left(3\right)-f\left(1\right)=\frac{25\cdot3^3}{3}-\frac{25\cdot1^3}{3}=\frac{650}{3}$

321

$f\left(1\right)-f\left(0\right)=e-1$

$f\left(e\right)-f\left(\frac{1}{e}\right)=2{,}35$

322

$\int_0^13e^xdx=3\cdot\int_0^1e^xdx=3\cdot\bigg/_{\!\!\!\!\!0}^1e^x=3e^x$

$f\left(1\right)-f\left(0\right)=3e-3$

$\int_0^{\pi}\sin xdx=\bigg/_{\!\!\!\!\!0}^{\pi}-\cos x$
$f\left(\pi\right)-f\left(0\right)=$

324

$4\frac{1}{3}$

$-4\frac{1}{3}$

$4\frac{1}{3}+\frac{4}{3}=\frac{13}{3}+\frac{4}{3}=\frac{17}{3}=5\frac{2}{3}$

$4$

$4\frac{1}{3}$

332

$\int_1^e\frac{1}{x}dx+\int_1^e\left(1-\frac{1}{x}\right)dx=\int_1^ex^{-1}dx+\int_1^e1-x^{-1}dx=\int_1^ex^{-1}-x^{-1}+1=\int_1^e1=\bigg/_{\!\!\!\!\!1}^ex$

$f\left(e\right)-f\left(1\right)=e-1$

$\int_0^1\left(3x^2-2x+1\right)dx+\int_1^2\left(3x^2-2x+1\right)dx=\bigg/_{\!\!\!\!\!0}^1\left(x^3-x^2+x\right)+\bigg/_{\!\!\!\!\!1}^2\left(x^3-x^2+x\right)$

$=\bigg/_{\!\!\!\!\!0}^2x^3-x^2+x$

$f\left(2\right)-f\left(0\right)=6$

333

$\int_5^52x\sqrt[]{x^2+1}dx=0$

$\int_{-1}^1x\sin^2xdx+\int_{-1}^1x\cos^2xdx=\int_{-1}^1\left(x\sin^2x\right)+\left(x\cos^2x\right)dx=\int_{-1}^1\left(x\left(\sin^2x+\cos^2x\right)\right)dx=\int_{-1}^1xdx=\bigg/_{\!\!\!\!\!{-1}}^1\frac{1}{2}x^2$
$f\left(1\right)-f\left(-1\right)=0$

$\int_0^1\left(x-1\right)dx+\int_0^1\left(x^2-x\right)dx+\int_0^1\left(x^3-x^2\right)dx+...+\int_0^1\left(x^9-x^8\right)dx=\int_0^1\left(x-1+x^2-x+x^3-x^2+...+x^9-x^8\right)dx=\int_0^1\left(-1+x^9\right)dx=\bigg/_{\!\!\!\!\!0}^1-x+\frac{1}{10}x^{10}$
$f\left(1\right)-f\left(0\right)=-\frac{9}{10}$

334

a)
https://peda.net/id/82fb834ec95

Kun x<2, funktio saa negatiivisia arvoja, tällöin

$\left|2x-4\right|=-\left(2x-4\right)=-2x+4$

Kun x≥2, funktio saa positiivisia arvoja, tällöin

$\left|2x-4\right|=2x-4$

Eli tässä tapauksessa pitää laskea pinta-alat välillä [0,2] [2,3]

$\int_0^3\left|2x-4\right|dx=\int_0^2\left(-2x+4\right)dx+\int_2^3\left(2x-4\right)dx=\bigg/_{\!\!\!\!\!0}^3\left(-x^2+4x\right)+\bigg/_{\!\!\!\!\!0}^3\left(x^2-4x\right)=\left(-2^2+4\cdot2\right)-\left(-0^2+4\cdot0\right)+\left(3^2-4\cdot3\right)-\left(2^2-4\cdot2\right)=4+8+9-12-4+8=5$

b)
https://peda.net/id/8a70e5c4c95

Kun x≤-2 tai x≥2, funktio saa positiivisia arvoja, tällöin
$\left|x^2-4\right|=x^2-4$
Kun -2<x<2, funktio saa negatiivisia arvoja, tällöin
$\left|x^2-4\right|=-\left(x^2-4\right)=-x^2+4$
Eli tässä tapauksessa pitää laskea pinta-alat välillä [-3,-2] [-2,2] ja [2,3]
$\int_{-3}^3\left|x^2-4\right|=\int_{-3}^{-2}\left(x^2-4\right)dx+\int_{-2}^2\left(-x^2+4\right)dx+\int_2^3\left(x^2-4\right)dx$

$=\bigg/_{\!\!\!\!\!{-3}}^{-2}\left(\frac{1}{3}x^3-4x\right)+\bigg/_{\!\!\!\!\!{-2}}^2\left(-\frac{1}{3}x^3+4x\right)+\bigg/_{\!\!\!\!\!2}^3\left(\frac{1}{3}x^3-4x\right)$

$=\left(\left(\frac{1}{3}\cdot\left(-2\right)^3-4\cdot\left(-2\right)\right)-\left(\frac{1}{3}\cdot\left(-3\right)^3-4\cdot\left(-3\right)\right)\right)+\left(\left(-\frac{1}{3}2^3+4\cdot2\right)-\left(-\frac{1}{3}\left(-2\right)^3+4\cdot\left(-2\right)\right)\right)+\left(\left(\frac{1}{3}\cdot3^3-4\cdot3\right)-\left(\frac{1}{3}\cdot2^3-4\cdot2\right)\right)$

$=\left(\frac{16}{3}-3\right)+\left(\frac{16}{3}-\left(-\frac{16}{3}\right)\right)+\left(-3-\left(-\frac{16}{3}\right)\right)=\frac{46}{3}=15\frac{1}{3}$

3.1

301

$16{,}7-6{,}6=10{,}1$

302

a) Appletin avulla saattiin pinta-ala välillä [0,3], joka on siis $A\left(3\right)=21$ , pinta-ala välillä [0,1] on appletin mukaan

$A\left(1\right)=1$

Joten ylläolevien tietojen mukaan pinta-ala välillä [1,3] on

$21-1=20$

A-kohdan perusteella voidaan oleta, että pinta-ala välillä [1,3] on funktio A(3) ja A(1) erotus

Määritetään funktiot A(3) ja A(1)

$A\left(3\right)=3^3-3^2+3=21$

$A\left(1\right)=1^3-1^2+1=1$

$A\left(3\right)-A\left(1\right)=20$

Koska lauseen mukaan pinta-alafunktio A on funktion f eräs integraalifunktio, eli

$A'\left(x\right)=f\left(x\right)$

Derivoitaan funktio A(x)

$A'\left(x\right)=f\left(x\right)=3x^2-2x+1$

304

$A\left(x\right)=\frac{\left(1+x+1\right)\cdot x}{2}=\frac{x^2+2x}{2}=\frac{x^2}{2}+x$

$A'\left(x\right)=f\left(x\right)$

$A'\left(x\right)=$

Koska $A'\left(x\right)=f\left(x\right)$ , pinta-alafunktio A on funktion f eräs integraalifunktio, joten voidaan saada integroimalla f(x) kautta funktio A(x)
$A\left(x\right)=\int_{ }^{ }f\left(x\right)dx=\int_{ }^{ }\left(x+1\right)dx=\frac{1}{2}x^2+x+C{,}\ C\in\mathbb{R}$

$A\left(0\right)=\frac{1}{2}0^2+0+C=0$
$C=0$

$A\left(2\right)-A\left(1\right)=\frac{5}{2}=2\frac{1}{2}=2{,}5$

306

Koska $A'\left(x\right)=f\left(x\right)$ , pinta-alafunktio A on funktion f eräs integraalifunktio, joten voidaan saada integroimalla f(x) kautta funktio A(x)

$A\left(x\right)=\int_{ }^{ }f\left(x\right)dx=\int_{ }^{ }\left(x-1\right)dx=\frac{1}{2}x^2-x+C{,}\ C\in\mathbb{R}$

$A\left(2\right)=\frac{1}{2}2^2-2+C=2$

$C=0$

$A\left(5\right)-A\left(3\right)=7{,}5-1{,}5=6$

308

309

Tässä halutaan laskea funktion y nollakohdat

eli

$-x^2+x+2=0$

$x=-1\ tai\ x=2$ (Laskin)

eli pisteessö (-1,0) ja (2,0)

$\int_{-1}^2\left(-x^2+x+2=0\right)dx=\bigg/_{\!\!\!\!\!{-1}}^2\left(-1\cdot\frac{1}{2+1}x^{2+1}+1\cdot\frac{1}{1+1}x^{1+1}+2x\right)=\bigg/_{\!\!\!\!\!{-1}}^2\left(-\frac{1}{3}x^3+\frac{1}{2}x^2+2x\right)$

$=\left(-\frac{1}{3}\cdot2^3+\frac{1}{2}\cdot2^2+2\cdot2\right)-\left(-\frac{1}{3}\cdot\left(-1\right)^3+\frac{1}{2}\cdot\left(-1\right)^2+2\cdot\left(-1\right)\right)=\frac{10}{3}-\left(-\frac{7}{6}\right)=\frac{9}{2}=4\frac{1}{2}$

311

$\int_0^3\left(3t+4\right)dt=\bigg/_{\!\!\!\!\!0}^3\left(3\cdot\frac{1}{1+1}t^{1+1}+4t\right)=\bigg/_{\!\!\!\!\!0}^3\left(\frac{3}{2}t^2+4t\right)$

$=\left(\frac{3}{2}\cdot3^2+4\cdot3\right)-\left(\frac{3}{2}\cdot0^2+4\cdot0\right)=25{,}5mm$

jos x-akseli on smalla ajan kuvaava t-akseli, veden määrä kolmen ensimmäisen tunnin aikana on siis sama asia kuin f kuvaajan ja t-akselin rajoittaman alueen pinta-ala välillä [0,3]

ja se on 25.5mm

c)C

312

$\int_0^a\left(3x^2-4x+2\right)dx=4$

$a=2$ (Laskin)

314

$\int_{ }^{ }\left(4x-1\right)dx=2x^2-x+C$

$f\left(1\right)=3$

$2\cdot1^2-1+C=3$

$2-1+C=3$
$C=2$

eli

$f\left(x\right)=2x^2-x+2$

Halutaan laskea kuvaajan f ja x-akselin rajoittaman alueen pinta-ala välillä [1,4]

$\int_1^4\left(2x^2-x+2\right)dx=\frac{81}{2}=40\frac{1}{2}$ (Laskin)

2.2

238

$\int_{ }^{ }e^{2x}=\frac{1}{2}e^{2x}+C$

$H\left(0\right)=\frac{1}{2}e^{2\cdot0}+C$
$\frac{1}{2}e^{2\cdot0}+C=-1$

$C=-\frac{3}{2}$

243

$\int_{ }^{ }-6\sin3x\ dx=\int_{ }^{ }-2\cdot3\cdot\sin3x\ dx=-2\int_{ }^{ }3\cdot\sin3x\ dx=-2\cdot\left(-\cos3x\right)+C=2\cos3x+C$

$G\left(\frac{\pi}{2}{,}1\right)=2\cos\left(3\cdot\frac{\pi}{2}\right)+C$

$2\cos\left(3\cdot\frac{\pi}{2}\right)+C=1$
$2\cdot0+C=1$

$C=1$

$G\left(x\right)=2\cos3x+1$

$2\cos3x+1=2$
$2\cos3x=1$
$\cos3x=\frac{1}{2}$

$3x=\pm\frac{\pi}{3}+n\cdot2\pi\ \ \ \ \ \left|\right|:3$

$x=\pm\frac{\pi}{9}+n\cdot\frac{2\pi}{3}{,}\ n\in\mathbb{Z}$

250

Koska 2,5 tunti on 150 min, on jäljellä n. 6 eliötä/min

$g'\left(x\right)=54{,}06\cdot e^{-0{,}01x}$
$g\left(x\right)=\int_{ }^{ }54{,}06\cdot e^{-0{,}01x}dx=-3624{,}53e^{-0{,}01x}+C$

Koska tunti on 60 min

$g\left(0\right)=-3624{,}53e^{-0{,}01\cdot60}+C=500$
$C=4124.53$

$g\left(60\right)=2135.3457606281...\approx2135$

257
$\int_{ }^{ }\tan xdx=\int_{ }^{ }\left(\frac{\sin x}{\cos x}\right)dx=\int_{ }^{ }\left(\sin x\cdot\left(\cos x\right)^{-1}\right)dx=-\int_{ }^{ }-\sin x\left(\cos x\right)^{-1}dx$

$s\left(x\right)=\cos x{,}\ s'\left(x\right)=-\sin x{,}\ U=\ln\left|x\right|$

$=-\ln\left|\cos x\right|+C$

Koska $\cos x>0{,}\ -\frac{\pi}{2}<x<\frac{\pi}{2}$
$=-\ln\left(\cos x\right)+C$

2.1

145

$\int_{ }^{ }\frac{1}{x^3}dx=\int_{ }^{ }x^{-3}dx=1\cdot\frac{1}{-3+1}x^{-3+1}+C$

$=-\frac{1}{2x^{-2}}+C{,}\ C\in\mathbb{R}$

$\int_{ }^{ }\frac{9}{x^2}dx=\int_{ }^{ }9x^{-2}dx=9\cdot\frac{1}{-2+1}x^{-2+1}+C$

$=-9x^{-1}+C=-\frac{9}{x}+C{,}\ C\in\mathbb{R}$

$\int_{ }^{ }\frac{4}{x}dx=\int_{ }^{ }4\cdot\frac{1}{x}dx=4\cdot\int_{ }^{ }\frac{1}{x}dx=4\ln x+C{,}\ C\in\mathbb{R}$

147

$\int_{ }^{ }\frac{x+2}{x}dx=\int_{ }^{ }\frac{x}{x}+\frac{2}{x}dx=\int_{ }^{ }\frac{2}{x}+1dx=\int_{ }^{ }2\cdot\frac{1}{x}+1dx=2\int_{ }^{ }\frac{1}{x}+1dx=2\ln x+x+C{,}\ C\in\mathbb{R}$

$f\left(x\right)=2\ln x+x-e{,}\ x>0$

149

$\int_{ }^{ }\frac{1}{2x^5}dx=\int_{ }^{ }\frac{1}{2}\cdot\frac{1}{x^5}dx=\frac{1}{2}\int_{ }^{ }x^{-5}dx=\frac{1}{2}\cdot\frac{1}{-5+1}x^{-5+1}+C=\frac{1}{2}\cdot\frac{1}{-4}\cdot\frac{1}{x^4}+C$

$=-\frac{1}{8x^4}+C{,}\ C\in\mathbb{R}$

$\int_{ }^{ }x^2\sqrt[]{x}dx=\int_{ }^{ }x^2x^{\frac{1}{2}}dx=\int_{ }^{ }x^{\frac{5}{2}}dx=\frac{1}{\frac{5}{2}+1}x^{\frac{7}{2}}+C$

$=\frac{2}{7}x^{\frac{7}{2}}+C=\frac{2}{7}x^{\frac{6}{2}}x^{\frac{1}{2}}+C=\frac{2}{7}x^3\sqrt[]{x}+C{,}\ C\in\mathbb{R}$

$\int_{ }^{ }\frac{dx}{2\sqrt[]{x}}=\int_{ }^{ }\frac{1}{2\sqrt[]{x}}dx=\int_{ }^{ }\frac{1}{2}\cdot\frac{1}{\sqrt[]{x}}dx=\frac{1}{2}\int_{ }^{ }\frac{1}{x^{\frac{1}{2}}}dx=\frac{1}{2}\cdot\int_{ }^{ }x^{-\frac{1}{2}}dx$

$=\frac{1}{2}\cdot\frac{1}{-\frac{1}{2}+1}x^{-\frac{1}{2}+1}+C=\frac{1}{2}\cdot2x^{\frac{1}{2}}+C=x^{\frac{1}{2}}+C=\sqrt[]{x}+C{,}\ C\in\mathbb{R}$

1.2

125

$\int_{ }^{ }\left(6x^2-4x+1\right)dx=6\cdot\frac{1}{2+1}x^{2+1}-4\cdot\frac{1}{1+1}x^{1+1}+1\cdot x+C=\frac{6}{3}x^3-\frac{4}{2}x^2+x$

$=2x^3-2x^2+x+C{,}\ C\in\mathbb{R}$

$F\left(2\right)=2\cdot2^3-2\cdot2^2+2+C=12$

$2\cdot8-2\cdot4+2+C=12$
$16-8+2+C=12$
$10+C=12$
$C=2$
$F\left(x\right)=2x^3-2x^2+x+2$

126

$\int_{ }^{\cdot}\left(8x^5-\frac{3}{5}x^2+2\right)dx=8\cdot\frac{1}{5+1}x^{5+1}-\frac{3}{5}\cdot\frac{1}{2+1}\ x^{2+1}+2\cdot x+C$

$=\frac{4}{3}x^6-\frac{1}{5}x^3+2x+C{,}\ C\in\mathbb{R}$

$\int_{ }^{ }x\left(3x+2\right)dx=\int_{ }^{ }\left(3x^2+2x\right)dx=3\cdot\frac{1}{2+1}x^{2+1}+2\cdot\frac{1}{1+1}x^{1+1}+C$

$=x^3+x^2+C{,}\ C\in\mathbb{R}$

$\int_{ }^{ }\left(x+2\right)\left(3x-4\right)dx=\int_{ }^{ }\left(3x^2+2x-8\right)dx=3\cdot\frac{1}{2+1}x^{2+1}+2\cdot\frac{1}{1+1}x^{1+1}-8\cdot\frac{1}{0+1}x^{0+1}+C$

$=x^3+x^2-8x+C{,}\ C\in\mathbb{R}$

128

$f\left(x\right)=\frac{1}{2}x-1$

$\int_{ }^{ }\left(\frac{1}{2}x-1\right)dx=\frac{1}{2}\cdot\frac{1}{1+1}x^{1+1}-1\cdot\frac{1}{0+1}x^{0+1}+C$
$=\frac{1}{4}x^2-x+C{,}\ C\in\mathbb{R}$

$x=2$

1.1

105

$F_2$ , koska sen muutosnopeus välillä [-1,1] on negatiivinen, vastaavan muutosnopeuksen voidaan nähdä myös kuvaajasta f(x).

106

Osoitetaan, että

$F'\left(x\right)=f\left(x\right)$

Derivoidaan funktio F(x)

$F'\left(x\right)=D\left(\frac{1}{3}x^6-\frac{2}{5}x^5+3x^2-\frac{2}{3}\right)=2x^5-2x^4+6x=f\left(x\right)$

Oletetaa, että funktio f(x) toinen integraalifunktio on $F_2$

Jos katsotaan funktio $F_2$ integraalilauseen avulla,

$G\left(x\right)=F\left(x\right)+C$

$G\left(x\right)=F_2\left(x\right)$

$F\left(x\right)=f\left(x\right)$
$C=\mathbb{R}$

Tässä tapauksessa C voi olla mikä tahanssa realiluku,

Esim.

$F_2'\left(x\right)=f\left(x\right)$
$F_2\left(x\right)=\frac{1}{3}x^6-\frac{2}{5}x^5+3x^2+1{,}\ C=1$

108

$F'\left(x\right)=f\left(x\right)$

$F\left(x\right)=x^4+C{,}\ C=\mathbb{R}$

Koska funktio F(x) kulkee pisteen (0,1/2) kautta,

$F\left(0\right)=0^4+C=\frac{1}{2}$

$0^4+C=\frac{1}{2}$
$C=\frac{1}{2}$

$F\left(x\right)=x^4+\frac{1}{2}$

$F'\left(x\right)=f\left(x\right)$
$F\left(x\right)=x^5+C{,}\ C=\mathbb{R}$
Koska funktio F(x) kulkee pisteen (0,1/2) kautta,
$F\left(0\right)=0^5+C=\frac{1}{2}$
$0^5+C=\frac{1}{2}$
$C=\frac{1}{2}$

$F\left(x\right)=x^5+\frac{1}{2}$

$F'\left(x\right)=f\left(x\right)$
$F\left(x\right)=e^x+C{,}\ C=\mathbb{R}$
Koska funktio F(x) kulkee pisteen (0,1/2) kautta,
$F\left(0\right)=e^0+C=\frac{1}{2}$
$e^0+C=\frac{1}{2}$
$1+C=\frac{1}{2}$

$C=-\frac{1}{2}$

$F\left(x\right)=e^x-\frac{1}{2}$

109

$F_1\left(x\right)=x^2+1$

$F_2\left(x\right)=x^2+2$
$F_3\left(x\right)=x^2+3$

$F_1\left(3\right)-F_1\left(2\right)=\left(3^2+1\right)-\left(2^2+1\right)=10-5=5$

$F_2\left(3\right)-F_2\left(2\right)=\left(3^2+2\right)-\left(2^2+2\right)=11-6=5$
$F_3\left(3\right)-F_3\left(2\right)=\left(3^2+3\right)-\left(2^2+3\right)=12-7=5$
Huomasin, että funktioiden on ratkaisu on kaikille kolmelle funktiolle 5

Kyllä, koska lakussa plus ja miinus merkit kumoavat toisensa.