4.1

401

$f\left(x\right)=x^2-1$

$A=-\int_{-1}^1f\left(x\right)dx=-\bigg/_{\!\!\!\!\!{-1}}^1\left(\frac{1}{3}x^3-x\right)$

$A=-\left(f\left(1\right)-f\left(-1\right)\right)=-\left(\frac{1}{3}-1-\left(-\frac{1}{3}\right)-1\right)=-\left(-\frac{4}{3}\right)=\frac{4}{3}$
b)

$f\left(x\right)=x^3-2x^2$

$A=-\int_0^2\left(x^3-2x^2\right)=-\bigg/_{\!\!\!\!\!0}^2\left(\frac{1}{4}x^4-\frac{2}{3}x^3\right)$

$A=-\left(\frac{1}{4}\cdot2^4-\frac{2}{3}\cdot2^3-0\right)=-\left(-\frac{4}{3}\right)=\frac{4}{3}$

403

$f\left(x\right)=x^2-4x-5$

$x=5$ tai $x=-1$ (Laskin)

$f\left(2\right)=2^2-8-5=-9$

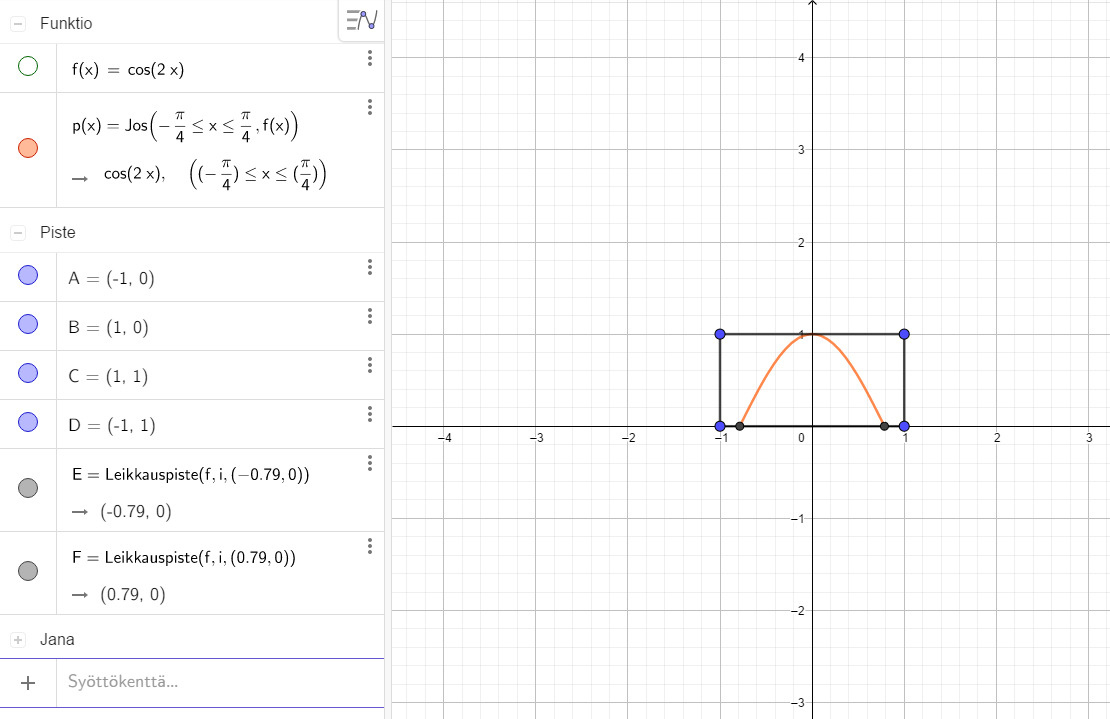
Pinta-alaa rajaa y-akseli, joten väli on x=0

Pinta-alaa rajaa suora x=1, joten kysytty pinta-ala on välillä [0,1]

Edellisessä tehtävässä lasketun nollakohdan puolivälin arvo on negatiivinen, joiten rajattu alue on myös negatiivinen(ylöspäin aukeava)

Tällöin

$A=-\int_0^1f\left(x\right)dx=-\bigg/_{\!\!\!\!\!0}^1\left(\frac{1}{3}x^3-2x^2-5x\right)$

$A=-\left(\frac{1}{3}\cdot1^3-2\cdot1^2-5\cdot1-0\right)=-\left(-\frac{20}{3}\right)=\frac{20}{3}=6\frac{2}{3}$

404

$\int_0^{2\pi}f\left(x\right)dx=\bigg/_{\!\!\!\!\!0}^{2\pi}\left(-\cos x\right)$

$=-1-\left(-1\right)=0$

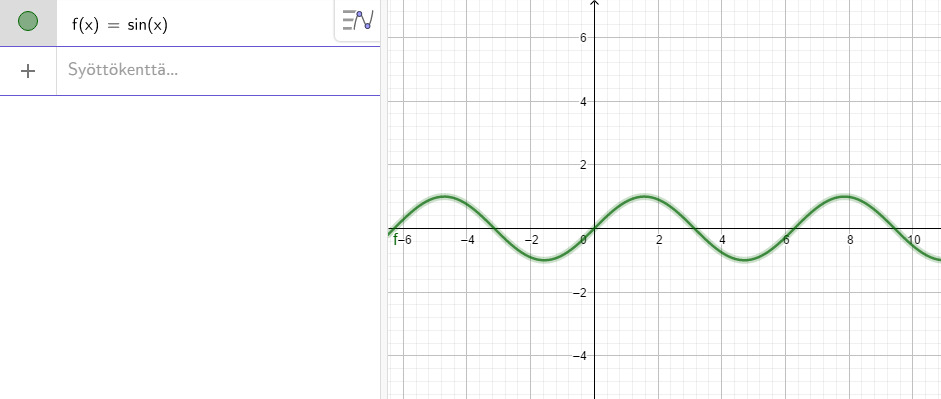
Tehtävässä halutaan laskea pinta-alaa välillä [0,2π]

Merkkikaavion perusteella voidaan oleta, että funktio välillä [0,π] on positiivinen, ja [π,2π] negatiivinen

$A=\int_0^{\ 2\pi}\left|\sin x\right|dx=4$ (laskin)

407

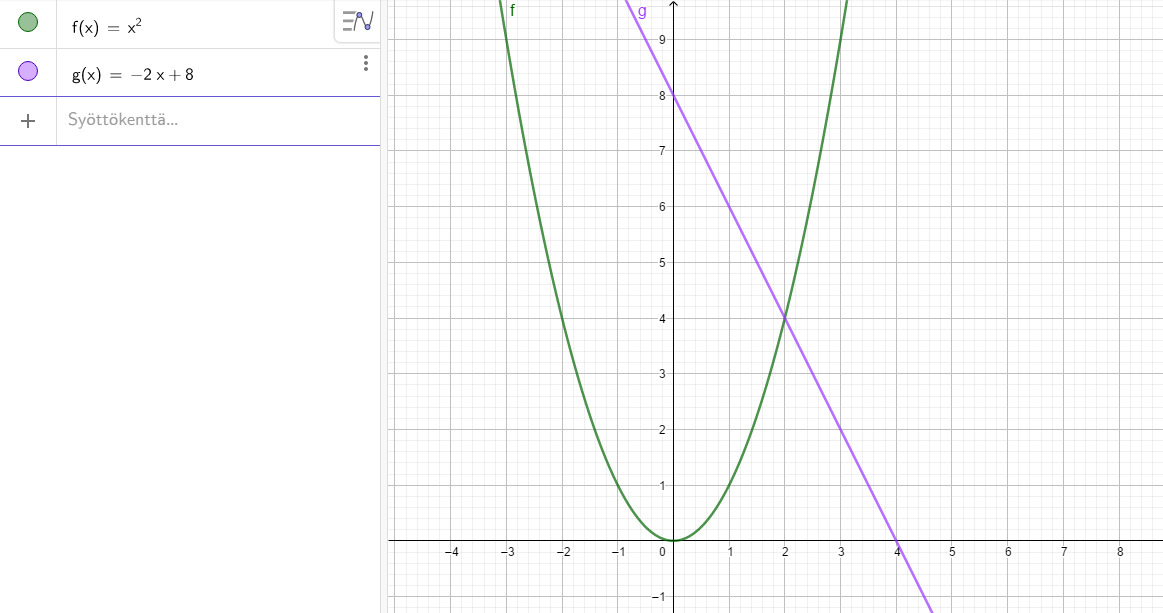
Suora 2x+y-8=0 on ratkaistussa muodossa y=-2x+8. Paraabeli y=x²

Lasketaan ensi funktioiden leikkauspisteet

$-2x+8=x^2\ \ \ \ \$

$-x^2-2x+8=0$
$x=−4$ tai $x=2$

Ja seuraavaksi funktioiden nollakohdat

$-2x+8=0$
$-2x=-8\ \ \ \ \ \left|\right|:\left(-2\right)$
$x=4$

$x^2=0$
$x=0$

Koska väli on positiivisella puolella, leikkauspiste pisteessä x=-4 ei huomioitaan.

Eli halutaan saada suora -2x+8 ja paraabelin x² pinta-ala välillä [0,4]

Tätä väliä voidaan jakaa kahteen eri osaa: [0,2] ja [2,4]

Lasketaan paraapelin avulla välin [0,2] pinta-ala ja suoran avulla pinta-ala välillä [2,4]

$A_1=\int_0^2f\left(x\right)dx=\bigg/_{\!\!\!\!\!0}^2\left(\frac{1}{3}x^3\right)$

$A_1=\left(\frac{1}{3}2^3-0\right)=\frac{8}{3}$

$A_2=\int_2^4\left(-2x+8\right)dx=\bigg/_{\!\!\!\!\!2}^4\left(-x^2+8x\right)$
$A_2=\left(\left(-4^2+8\cdot4\right)-\left(-2^2+8\cdot2\right)\right)=\left(16-12\right)=4$
$A_{kok}=\frac{8}{3}+4=\frac{20}{3}=6\frac{2}{3}$

408

a) $-3$
b) $\frac{5}{2}$
c) $\frac{5}{2}+\left(-3\right)=-\frac{1}{2}$

d) $-\frac{2}{3}$
e)

409

Käyrä muodostaa akselien kanssa alueen, joten ensimmäinen aluetta rajaava suora on kohdassa x=0

Toisen suoran saadaan laskemalla käyrän nollakohdat

$e^x-2=0$

$e^x=2$
$\log_e2=x$
$x=\ln2$

Koska aro kohdassa x=ln2 on 0, tarvitaan kohdan x=0 arvo

$e^0-2=1-2=-1$

Koska arvo on negatiivinen, janojen rajaama alue on negatiivinen

Halutaan laskea se alue joka on välillä [0,ln2]

$A=-\int_0^{\ln2}\left(e^x-2\right)dx=-\bigg/_{\!\!\!\!\!0}^{\ln2}\left(e^x-2x\right)$

$A=-\left(e^{\ln2}-2\cdot\left(\ln2\right)-e^0-2\cdot0\right)=\left(2-2\ln2-1\right)=2\ln2-1$

Aluetta rajaa suorat x=3, x-akseli ja funktio f(x)

Aluetta rajaava suora on funktio f(x) ja x-akseli leikkauspisteellä

Lasketaan funktion nollakohdat

$\frac{1}{x}-1=0$
$\frac{1}{x}=1$

$x=1$

Koska aro kohdassa x=1 on 0, tarvitaan kohdan x=3 arvo
$\frac{1}{3}-1=-\frac{2}{3}$
Arvo on negatiivinen, janojen rajaama alue on negatiivinen
Halutaan laskea se alue joka on välillä [1,3]
$A=-\int_1^3\left(\frac{1}{x}-1\right)dx=-\bigg/_{\!\!\!\!\!1}^3\left(\ln\left|x\right|-x\right)$
$A=-\left(\ln3-3-\left(-1\right)\right)=-\left(\ln3-2\right)=2-\ln3$

410

Lasketaan funktion f(x) nollakohdat

$\sqrt[]{3-x}=0$

$3-x=0$
$-x=-3$
$x=3$

Lasketaan suoran y nollakohta

$x+3=0$
$x=-3$

Lasketaan funktioiden leikkaupisteet

$\sqrt[]{3-x}=x+3$

$x=-1$ (laskin)

Koska suora on nouseva, ja funktiolla f(x) on vain ratkaisuja kun x≤0, joten alue on positiivinen

Alueet ovat välillä [-3,-1] ja [-1,3]

$A_1=\int_{-3}^{-1}\left(x+3\right)dx=\bigg/_{\!\!\!\!\!{-3}}^{-1}\left(\frac{1}{2}x^2+3x\right)$

$A_1=f\left(-1\right)-f\left(-3\right)=2$
$A_2=\int_{-1}^3\left(\sqrt[]{3-x}\right)dx=\int_{-1}^3\left(\left(3-x\ \right)^{\frac{1}{2}}\right)dx=\bigg/_{\!\!\!\!\!{-1}}^3\left(\frac{-2\left(3-x\right)^{\frac{3}{2}}}{3}\right)$
$A_2=f\left(3\right)-f\left(-1\right)=\frac{16}{3}$

$A_{kok}=2+\frac{16}{3}=\frac{22}{3}=7\frac{1}{3}$

413

Lasketaan suorakulmion pinta-ala
$A_s=2\cdot1=2$
Käyrän nollakohdat välillä [-1,1] on
$\cos2x=0{,}\ \left[-1{,}1\right]$
$x=\frac{\pi}{4}\ ja\ x=-\frac{\pi}{4}$ (laskin)

Käyrän pinta-ala välillä [ $-\frac{\pi}{4}{,}\ \frac{\pi}{4}$ ]