4.2

431

$x^2+2x-5=7-x^2$
$x=-3\ tai\ x=2$

Otetaan testipisteeksi välin keskiarvo $-\frac{1}{2}$

$f\left(x\right)=x^2+2x-5-7$

$g\left(x\right)=7-x^2$

$f\left(-\frac{1}{2}\right)=-\frac{23}{4}$ (Laskin)

$g\left(-\frac{1}{2}\right)=\frac{27}{4}$ (Laskin)

Laskujen perusteella funktio g(x) on ylempänä, koska sen arvo pisteessä $x=-\frac{1}{2}$ on suurempi

$A=\int_{-3}^2\left(f\left(x\right)-g\left(x\right)\right)=\frac{125}{3}=41\frac{2}{3}$

432

$x^3-x^2-x=x$

$x=−1\ tai\ x=0\ tai\ x=2$ (laskin)

f(x) on ylempänä välillä ]-1,0[, ja g(x) on ylempänä välillä ]0,2[

$A_1=\int_{-1}^0\left(f\left(x\right)-g\left(x\right)\right)=\frac{5}{12}$
$A_2=\int_0^2\left(g\left(x\right)-f\left(x\right)\right)=\frac{8}{3}$
$A_{kok}=\frac{5}{12}+\frac{8}{3}=\frac{37}{12}=3\frac{1}{12}$

433

$A_1=\int_{-3}^1f\left(x\right)-g\left(x\right)dx=10-2=8$

$A=\int_1^7f\left(x\right)-g\left(x\right)=23-\left(-5\right)=28$

$A=28+8=36$

434

Lasketaan funktioiden leikkauspisteet

$x+6=x^2$

$-x^2+x+6=0$

$x=\frac{-1\pm\sqrt[]{1^2-4\cdot\left(-1\right)\cdot6}}{2\cdot\left(-1\right)}=\frac{-1\pm5}{-2}$
$x=\frac{-1+5}{-2}=-2\ tai\ x=\frac{-1-5}{-2}=3$

$\int_{-2}^3\left(-x^2+x+6\right)dx=\bigg/_{\!\!\!\!\!{-2}}^3-\frac{1}{3}x^3+\frac{1}{2}x^2+6x=\left(-\frac{1}{3}\cdot3^3+\frac{1}{2}\cdot3^2+6\cdot3\right)-\left(-\frac{1}{3}\cdot\left(-2\right)^3+\frac{1}{2}\cdot\left(-2\right)^2+6\left(-2\right)\right)=\frac{125}{6}=20\frac{5}{6}$

Suoran nollakohta on

$x+6=0$

$x=-6$

Lasketaan suora, y-akseli ja x-akseli rajaaman alueen pinta-ala

$A_a=\frac{6\cdot6}{2}=18$

Lasketaan paraapelin ja suoran rajaaman alueen pinta-ala välillä [-2,0]

$A_b=\int_{-2}^0\left(-x^2+x+6\right)dx=\bigg/_{\!\!\!\!\!{-2}}^0-\frac{1}{3}x^3+\frac{1}{2}x^2+6x=\left(-\frac{1}{3}\cdot0^3+\frac{1}{2}\cdot0^2+6\cdot0\right)-\left(-\frac{1}{3}\cdot\left(-2\right)^3+\frac{1}{2}\cdot\left(-2\right)^2+6\cdot\left(-2\right)\right)=7\frac{1}{3}$

$A_2=A_a-A_b=10\frac{2}{3}$

436

Lasketaan funktioiden leikkauspisteet

$e^x=e^{2x-1}$

$e^x-e^{2x-1}=0$
$x=1$

Lasketan funktioiden rajaama alueen pinta-ala välillä [0,1]

$\int_0^1\left(e^x-e^{2x-1}\right)dx=\frac{\left(e^2-2e+1\right)\cdot e^{-1}}{2}$

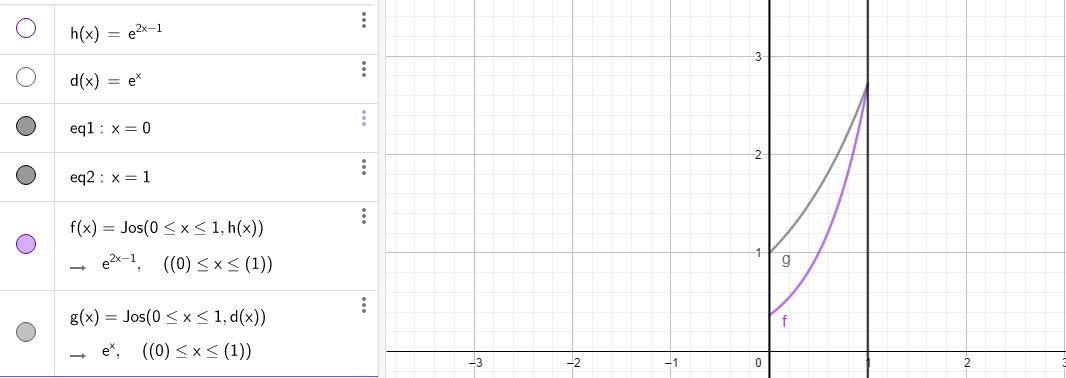
438

Leikkauskohdat

$\sin x=\cos x$

$\frac{\sin x}{\cos x}=1$
$\tan x=1$
$x=\frac{\pi}{4}+n\cdot\pi$

Leikkauskohdista välillä 0≤x≤π/2 on x=π/4

Alue koostuu kahdesta osasta. Välillä [0,π/4] käyrän sinx ja x-akselin rajaamasta osasta ja välillä [π/4,π/2] käyrän cosx ja x-akselin rajaamasta osasta

Käyrien rajoittaman alueen pinta-ala on

$\int_0^{\frac{\pi}{4}}\left(\sin x\right)dx+\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\left(\cos x\right)dx=\bigg/_{\!\!\!\!\!0}^{\frac{\pi}{4}}\left(-\cos x\right)+\bigg/_{\!\!\!\!\!{\frac{\pi}{4}}}^{\frac{\pi}{2}}\left(\sin x\right)$
$=\left(-\cos\frac{\pi}{4}+\cos0\right)+\left(\sin\frac{\pi}{2}-\sin\frac{\pi}{4}\right)$
$=\left(-\frac{1}{\sqrt[]{2}}+1\right)+\left(1-\frac{1}{\sqrt[]{2}}\right)$
$=2-\sqrt[]{2}$

Käyrien ja y-akselin väliin jäävä alue on käyrien y=sinx ja y=cosx väliin välillä [0,π/4] jäävä alue

Käyrien väliin jäävä pinta-ala on

$A=\int_0^{\frac{\pi}{4}}\left(\cos x-\sin x\right)dx=\bigg/_{\!\!\!\!\!0}^{\frac{\pi}{4}}\left(\sin x+\cos x\right)$

$=\left(\sin\frac{\pi}{4}+\cos\frac{\pi}{4}\right)-\left(\sin0+\cos0\right)$
$=\left(\frac{1}{\sqrt[]{2}}+\frac{1}{\sqrt[]{2}}\right)-\left(0+1\right)=\frac{^{\left(\sqrt[]{2}\right)}2}{\sqrt[]{2}}-1=\frac{2\sqrt[]{2}}{2}-1=\sqrt[]{2}-1$

443

$\int_{-1}^1\left(\left(-x^2+1\right)-\left(x+b\right)\right)dx=\bigg/_{\!\!\!\!\!{-1}}^1\left(\left(-\frac{1}{3}x^3+x\right)-\left(\frac{1}{2}x^2+bx\right)\right)=\bigg/_{\!\!\!\!\!{-1}}^1\left(-\frac{1}{3}x^3-\frac{1}{2}x^2+x-bx\right)$

$A=\left(-\frac{1}{3}-\frac{1}{2}+1-b\right)-\left(\frac{1}{3}-\frac{1}{2}-1+b\right)=\frac{4}{3}-2b$

$\frac{4}{3}-2b=8$

$-2b=\frac{20}{3}\ \ \ \ \ \left|\right|:\left(-2\right)$
$b=-\frac{10}{3}=-3\frac{1}{3}$