Tilavuus

Tilavuus

  • Pituus on yksiulotteinen (vain yhteen suuntaan)
  • Pinta-ala on kaksiulotteinen (2D, two dimensional)
  • Tilavuus on kolmiulotteinen (3D)

Yksikönmuunnoksia

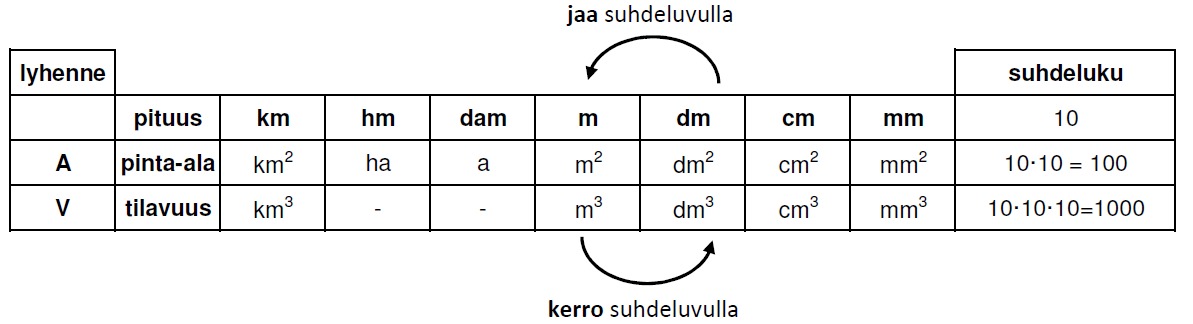
Pituus, pinta-ala ja tilavuus

  • Kiinnitä erityistä huomiota suhdelukuun!
  • pituus: suhdeluku 10
    • esim. 1 cm = 10 mm

  • pinta-ala: suhdeluku 100 (10 · 10)
    • 1 cm²  = 10 mm · 10 mm = 100 mm²

  • tilavuus: suhdeluku 1000 (10 · 10 · 10)
    • 1 cm³ = 10 mm · 10 mm · 10 mm = 1000 mm³
  • Riittää kun opettelet pituuden yksiköt, loput voi päätellä

Vetomitat

  • Litroihin perustuvissa mitoissa suhdeluku on taas hämäävästi 10 vaikka kyse on tilavuuksista.
  • Aika pitkälle pääsee kun opettelee mitä m3, dm3 ja cm3 on litroina.

Kuutio

Tilavuus


  • Pinta-ala lasketaan [[$ a \cdot b $]] (taso)
  • Tilavuuden voi ajatella koostuvan päällekäisistä tasoista
  • Kun tasoja laitetaan paljon päällekäin, ne täyttävät lopulta kolmiulotteisen tilan

  • Kuution (tai minkä tahansa suorakulmaisen särmiön) tilavuus lasketaan siis [[$$ V = a \cdot b \cdot c $$]]
  • Koska kuution kaikki sivut ovat yhtä pitkiä ([[$ a = b = c $]]) voidaan myös sanoa, että [[$$ V = a \cdot a \cdot a =a^3 $$]]

Pinta-ala

  • Kuutio muodostuu (nimensä mukaisesti) kuudesta samanlaisesta sivusta eli tahkosta. Siksi kuution kokonaispinta-ala voidaan laskea kertomalla yhden tahkon pinta-ala kuudella eli [[$ A_{kuutio} = 6 \cdot a^2 $]]

Suorakulmainen särmiö

Suorakulmainen särmiö
  • On "perinteinen laatikko"
  • Sen kaikki kulmat ovat 90°
    • eli kaikki tahkot ovat suorakulmioita

Tilavuus

  • Tilavuus lasketaan kertomalla kaikki kolme pituutta keskenään [[$$ V=a \cdot b \cdot c $$]]
    • yleensä pituudet erotetaan toisistaan termeillä korkeus, leveys ja pituus (tai syvyys)
    • ei ole mitään väliä mitä suuntaa kutsuu esim. leveydeksi

Pinta-ala


  • Särmiössä on kuusi tahkoa
  • Vastakkaiset tahkot ovat aina saman kokoiset
    • Esim. pohjan pinta-ala lasketaan [[$ A_{pohja} = a \cdot b $]], kansi on saman kokoinen eli [[$ A_{pohja+kansi}=2 \cdot a \cdot b $]]
  • Koko särmiön pinta-ala saadaan siis laskettua kun vastakkaisten tahkojen pinta-alat kerrotaan kahdella ja lasketaan yhteen [[$$ A=2\cdot a \cdot b + 2\cdot a \cdot c + 2\cdot b \cdot c $$]]