4.1 Lämpökapasiteetti ja ominaislämpökapasiteetti
Lämpökapasiteetti
Kaikessa aineessa tapahtuu lämpöliikettä, koska aine ei voi olla absoluuttisessa nollapisteessä. Lämpöliikkeeseen on varastoituneena energiaa, samoin aineen rakenneosien välisiin sidoksiin. Yleensä varastoituneen energian määrä ei ole keskeistä. Sen sijaan halutaan tietää, paljonko energiaa siirtyy kappaleesta tai aineesta toiseen. Energiaa siirtyy, kun kappale lämpenee, jäähtyy, tai sen olomuoto muuttuu. Siirtyvää lämpöenergiaa kutsutaan lämmöksi. Esimerkiksi aurinko siirtää lämpöä lumeen, saa sen sulamaan ja sulaneen veden edelleen lämpenemään.
Tutkitaan, miten veteen siirtynyt lämpö muuttaa sen lämpötilaa. Vesi on yleinen aine ja ihmiselle elintärkeä. Ihminen hyödyntää vettä lämpöilmiöihin liittyvissä sovelluksissa, ja veden ominaisuuksien tunteminen edesauttaa sovellusten suunnittelussa. Vettä käytetään mm. kaukolämpöverkossa lämpöenergian siirtäjänä.
Tutkimuksessa käytetään välineinä vedenkeitintä ja lämpömittaria. Vedenkeittimen teho [[$(P)$]] on sen pohjasta löytyvän arvokilven mukaan 2 000 W. Tehon määritelmän nojalla lasketaan lämpö [[$(Q)$]], jonka keitin siirtää veteen ajassa [[$(t)$]]:
[[$ \quad P=\dfrac{Q}{t} $]], joten [[$ Q = Pt $]].
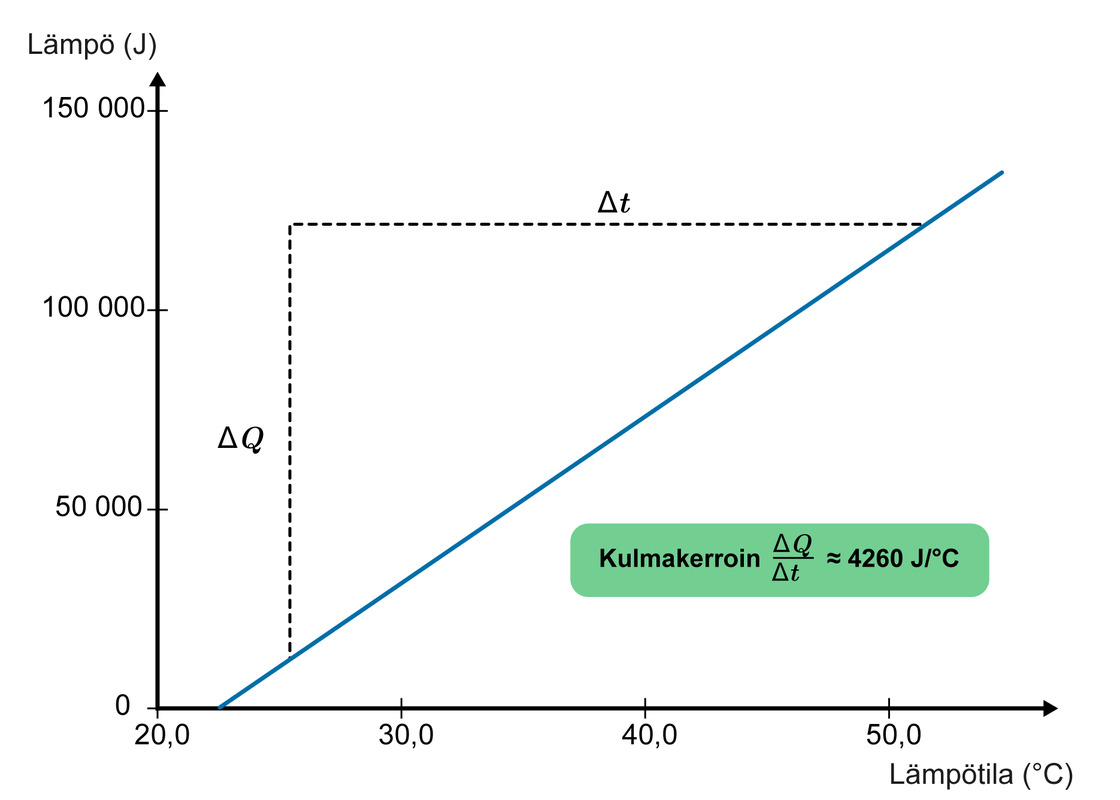
Alla olevalla videolla lämmitetään 1,00 kg vettä vedenkeittimessä samalla kun mitataan veden lämpötilaa. Vettä sekoitetaan mittauksen aikana, jotta lämpötila muuttuu kaikkialla astiassa tasaisesti. Vedenkeittimien tehon ja ajan avulla lasketaan veteen siirtynyt lämpö tehon määritelmää käyttäen. Mittaustulokset esitetään kuvaajana, jossa on lämmön riippuvuus lämpenemisajasta.
Mittaustulokset:
veden_lampokapasiteetin_mittaus.ods
veden_lampokapasiteetin_mittaus.cmbl
veden_lampokapasiteetin_mittaus.cap
Veteen tuodun lämmön ja lämpötilan välillä havaitaan lineaarinen riippuvuus. Jokainen asteen lämpeneminen vaatii yhtä paljon energiaa. Kulmakerroin ilmaisee, kuinka paljon energiaa tarvitaan yhteen kilogrammaan vettä, jotta veden lämpötila muuttuu yhden celsiusasteen. Kuvaajan kulmakertoimeksi saadaan 4 260 J/°C. Veteen tuotu lämpö varastoituu sen rakenneosasten lämpöliikkeeksi, ja kulmakerroin voidaan ymmärtää myös veden kykynä varastoida lämpöä. Suuretta kutsutaan lämpökapasiteetiksi. Mitä suurempi lämmitettävän kappaleen lämpökapasiteetti on, sitä enemmän energiaa tarvitaan sen lämmittämiseen ja sitä enemmän lämpöä se pystyy varastoimaan itseensä.
Kappaleen lämpötila voi myös laskea, jolloin se luovuttaa energiaa ympärilleen. Luovutettu energiamäärä on yhtä suuri kuin lämmittämisen yhteydessä vastaanotettu energiamäärä.
Kappaleen lämmetessä siihen siirtyvä energia on [[$ Q=C \Delta T $]].
- Kappaleen lämpökapasiteetti [[$(C)$]] kuvaa sen kykyä varastoida lämpöä.
- Kappaleen jäähtyessä se luovuttaa vastaavan määrän energiaa.
Ominaislämpökapasiteetti
Lämpökapasiteetilla kuvataan kappaleen kykyä sitoa energiaa itseensä. Yhden vesikilogramman lämpökapasiteetti oli edellisen mittauksen perusteella noin 4 200 J/°C. Vastaava mittaus voidaan toteuttaa suuremmalle määrälle vettä. Jos vettä on enemmän, sen lämmittämiseen samaan loppulämpötilaan kuluu pidempi aika. Energiaa on siirrettävä enemmän, eli isomman vesimäärän lämpökapasiteetti on suurempi. Veden lämmittämiseen tarvittava energiamäärä kasvaa samassa suhteessa kuin massa, koska energiaa on siirrettävä yhä useammalle rakenneosaselle.
Lämpökapasiteetti ei ole kätevä suure aineiden vertailuun, koska sen arvo riippuu sekä aineesta että sen määrästä. Tarvitaan suure, joka kertoo aineelle ominaisen kyvyn varastoida energiaa. Ominaislämpökapasiteetti [[$(c)$]] on aineen ominaisuus, joka ilmaisee aineen lämmittämiseen tarvittavan energian yhtä kilogrammaa kohden. Ominaislämpökapasiteetti on lämpökapasiteetin [[$(C)$]] ja massan [[$(m)$]] osamäärä.
[[$\quad c=\dfrac{C}{m}$]]
Koska edellä tehdyssä mittauksessa oli vettä yksi kilogramma, veden ominaislämpökapasiteetti on mittauksen perusteella [[$4\, 200 \, \dfrac{\text{J}}{\text{kg}\cdot \text{°C}} $]]. Veden lämpökapasiteetti kilogrammaa kohden on tarkemmin mitattuna [[$4\,190\, \dfrac{\text{J}}{\text{kg}\cdot \text{°C}} $]]. Mittauksen virhe on voinut aiheutua siitä, että kaikki vedenkeittimen tuottama energia ei ole siirtynyt veteen, vaan osa energiasta siirtyy vedenkeittimen kuoreen ja edelleen ympäristöön.
Lämpökapasiteetti liittyy kappaleen ja ominaislämpökapasiteetti aineen lämpötilan muutokseen. Ominaislämpökapasiteetti on jokaiselle aineelle ominainen suure. Yleisimpien aineiden ominaislämpökapasiteettien suuruudet löytyvät taulukkokirjasta. Aineilla on siis kullakin ominainen kyky varastoida lämpöä. Yksi kilogramma alumiinia, rautaa tai vettä tarvitsevat eri määrän energiaa lämmetäkseen yhden celsiusasteen. Vedellä on suuri ominaislämpökapasiteetti verrattuna moniin aineisiin. Se on esimerkiksi rautaan verrattuna lähes kymmenkertainen: kilo vettä tarvitsee 4 190 joulea lämmetäkseen yhden asteen, kun kilo rautaa lämpiää yhden asteen 450 joulella. Veden suuren ominaislämpökapasiteetin voi havaita veden hitaana lämpenemisenä auringonpaisteessa.
Aineen tai kappaleen lämpötila voi myös laskea, jolloin se luovuttaa energiaa ympärilleen. Luovutettu energiamäärä on yhtä suuri kuin lämmittämisen yhteydessä vastaanotettu energiamäärä.
Tietystä aineesta koostuvan kappaleen lämpökapasiteetti lasketaan aineen ominaislämpökapasiteetin ja massan tulona: [[$ C=cm $]].
- Ominaislämpökapasiteetti [[$(c)$]] kuvaa aineen kykyä varastoida energiaa.
Aineen lämmetessä siihen siirtyvä energia on [[$ Q=cm \Delta T $]].
- Aineen jäähtyessä se luovuttaa vastaavan määrän energiaa.
Lämpötasapaino
Lämpötilaerot pyrkivät aina tasoittumaan. Tällöin energiaa siirtyy erilämpöisten kappaleiden tai aineiden välillä. Jos eri lämpötiloissa olevat aineet muodostavat eristetyn systeemin, energiaa ei siirry systeemin ulkopuolelle. Systeemissä kokonaisenergia säilyy, mutta lämpöä voi siirtyä sen osien välillä. Lopulta systeemin osien lämpötilaerot tasoittuvat niin, että jäähtyvien osien luovuttamat lämmöt ovat yhtä suuret kuin lämpenevien osien vastaanottamat.
Eristettyä systeemiä voidaan kuvata seuraavanlaisella yhtälöllä.
[[$ \quad Q_{\text{luovutetut}}=Q_{\text{vastaanotetut}} $]]
Suljetun tai avoimen systeemin kokonaisenergia voi muuttua. Tällöin systeemiin tai siitä ulos siirtyvä energia lisätään yllä olevaan yhtälöön joko luovutettuihin tai vastaanotettuihin lämpöihin. Jos ympäristöstä tuodaan energiaa systeemiin, kyseessä on vastaanotettu lämpö. Vastaavasti ympäristöön siirtyvä lämpö on luovutettua energiaa.
Siirtyvää lämpöä laskettaessa lämpötilan muutos [[$ \Delta T $]] lasketaan alkulämpötilan ja loppulämpötilan erotuksena. Suuremmasta lämpötilan arvosta vähennetään pienempi, jolloin lämpötilan muutos [[$ \Delta T=T_{1}-T_{2} $]] on aina positiivinen. Siirtyvät lämmöt ovat näin ollen aina suuruudeltaan positiivisia.
Laskuissa voidaan käyttää lämpötilan yksikkönä joko celsiusasteita tai kelvineitä, koska molemmissa asteikoissa lämpötilan muutokset ovat yhtä suuret. Ominaislämpökapasiteetti tulee ilmaista käytettävien yksiköiden mukaisesti esimerkiksi jollain seuraavista tavoista:
[[$ \quad c_{\text{vesi}}=4\,190\,\dfrac {\text{J}}{\text{kg} \cdot \text{°C} }=4\,190\,\dfrac {\text{J}}{\text{kg} \cdot \text{K} }=4{,}190\, \dfrac {\text{kJ}}{\text{kg} \cdot \text{K} } $]].
Jos ominaislämpökapasiteetin yksikössä käytetään yksikköä kJ, myös siirtynyt lämpöenergia on yksikössä kJ. Energian yhteenlaskuissa kaikkien termien yksiköiden on oltava samat. Tämä on huomioitava, kun lämpöenergian suuruuksia lasketaan systeemin eri osille. Tällöin ominaislämpö- tai lämpökapasiteetille on valittava sama energian yksikkö.
Vaihtoehtoinen ratkaisutapa
Ratkaistavan yhtälön voi kirjoittaa myös siitä näkökulmasta, että lämpöä vastaanottavan systeemin osan lämpö on positiivinen ja luovuttavan systeemin osan lämpö negatiivinen. Esimerkiksi osa 1 vastaanottaa lämpöä, jolloin [[$Q_1$]] on positiivinen ja osa 2 luovuttaa lämpöä, jolloin [[$Q_2$]] on negatiivinen. Näiden summa on systeemin yhteensä vastaanottama tai luovuttama lämpö:
[[$\quad Q_1+Q_2=Q_\text{yht}$]]
Eristetylle systeemille summa on siten nolla.
[[$\quad Q_1+Q_2=0$]]
Positiivinen ja negatiivinen lämpö ovat seurausta positiivisesta tai negatiivisesta lämpötilan muutoksesta, joka lasketaan aina loppulämpötilan [[$T$]] ja alkulämpötilan [[$T_1$]] tai [[$T_2$]] erotuksena.
[[$ \quad \Delta T_1=T-T_{\text{1,alku}}$]] (positiivinen, jos lämpötila nousee)
[[$ \quad \Delta T_2=T-T_{\text{2,alku}}$]] (negatiivinen, jos lämpötila laskee)
Tässä ratkaisumenetelmässä ei tarvitse miettiä, mikä systeemin osa luovuttaa ja mikä vastaanottaa lämpöä. Esimerkki 3 on ratkaistu myös vaihtoehtoisella tavalla.
Pysähdy pohtimaan
Esimerkit
Esimerkki 1
 Kiukaan kivien lämpökapasiteetti on 14 000 J/°C. Kiukaan lämmitysteho on 4,5 kW.
Kiukaan kivien lämpökapasiteetti on 14 000 J/°C. Kiukaan lämmitysteho on 4,5 kW.
- Kuinka paljon energiaa vaatii kivien lämmitys 140 °C:n lämpötilaan? Kivien alkulämpötila on 15 °C.
- Kuinka kauan lämmitys kestää? Oletetaan, että 75 % kiukaan tehosta menee kivien lämmittämiseen.
Esimerkki 2
- Kuinka paljon energiaa vaatii, että 2,5 litraa vettä lämmitetään huoneenlämpöisestä (20,0 °C) kiehuvaksi?
- Jos yhtä paljon energiaa siirtyisi 2,5 kilogrammaan rautanauloja, kuinka paljon niiden lämpötila muuttuisi?
Esimerkki 3
Virvoitusjuomaa kaadetaan pakastimessa jäähdytettyyn lasiin, jonka lämpötila on -18 °C. Lasin lämpökapasiteetti on 130 J/K. Virvoitusjuoman alkulämpötila on 12 °C, massa 180 g ja ominaislämpökapasiteetti sama kuin vedellä. Mihin loppulämpötilaan systeemi päätyy, mikäli se oletetaan eristetyksi?
Esimerkki 4
Alumiininen punnus on lämpimässä vesihauteessa. Punnus siirretään eristettyyn astiaan, jossa on 350 g vettä. Kuvaajissa lämpötila 2 on lämpöhauteen ja lämpötila 1 eristetyn astian lämpötila.
- Millä hetkellä punnus siirrettiin?
- Määritä kuvaajien perusteella punnuksen massa.