Määritelmä
Olkoot a ja n kokonaislukuja. Kokonaisluku a on jaollinen luvulla n, jos on olemassa sellainen kokonaisluku q, että a=nq
Luku a on luvun n monikerta.
Luku n on luvun a tekijä.
Jakolasku ja jakoyhtälö
Kun suoritetaan jakolasku a:n, tulokseksi saadaan osamäärä ja jakojäännös
Jakoyhtälön avulla:
Jos jakolaskun a:n osamäärä on q ja jakojäännös r, niin

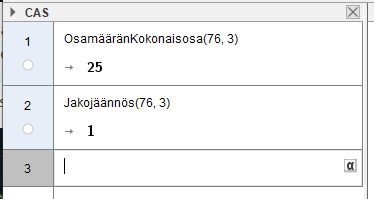
Ilmaise luku 76 muodossa
laskimella 76:3 = 25,3333...
eli

Jokainen kokonaisluku on muotoa 3q, 3q+1 tai 3q+2
Vastaavasti, kun mikä tahansa kokonaisluku jaetaan luvulla 2, jakojäännös on aina 0 tai 1
Siis jokainen kokonaisluku on näin ollen muotoa:
2q tai 2q+1
Binääri- eli kaksikantainen järjestelmä
Binäärijärjestelmässä lukujen kirjoittamiseen ei tarvita muita lukuja kuin 0 ja 1, sillä luvulla 2 jaettaessa jakojäännös on aina 0 tai 1
Esim. Kirjoitetaan binääriluku 1001011 kymmenjärjestelmän lukuna
1+2+8+64=75
Esim. Kirjoitetaan 38 binäärilukuna
Luku a on luvun n monikerta.
Luku n on luvun a tekijä.
Jakolasku ja jakoyhtälö
Kun suoritetaan jakolasku a:n, tulokseksi saadaan osamäärä ja jakojäännös
Jakoyhtälön avulla:
Jos jakolaskun a:n osamäärä on q ja jakojäännös r, niin
Ilmaise luku 76 muodossa
laskimella 76:3 = 25,3333...
eli

Jokainen kokonaisluku on muotoa 3q, 3q+1 tai 3q+2
Vastaavasti, kun mikä tahansa kokonaisluku jaetaan luvulla 2, jakojäännös on aina 0 tai 1
Siis jokainen kokonaisluku on näin ollen muotoa:
2q tai 2q+1
Binääri- eli kaksikantainen järjestelmä
Binäärijärjestelmässä lukujen kirjoittamiseen ei tarvita muita lukuja kuin 0 ja 1, sillä luvulla 2 jaettaessa jakojäännös on aina 0 tai 1
Esim. Kirjoitetaan binääriluku 1001011 kymmenjärjestelmän lukuna
1+2+8+64=75
Esim. Kirjoitetaan 38 binäärilukuna