1.1 Jaollisuus ja jakoyhtälö
113
a) 0
b) 1
c) 4
d) 2
b) 1
c) 4
d) 2
114
a) ei ole, pitäisi olla 2
b) -
b) -
112
a) 4*(-7)+1
b) 5*(-7)+2
c) 7*(-4)+5
d) 4*(-19)
b) 5*(-7)+2
c) 7*(-4)+5
d) 4*(-19)
109
2, 14, 26
108
11*12+8=140
118
a)
J= 1001010
U=1010101
U=1010101
R=1010010
I=1001001
10001101010100101010010100101000101
b)
1001011 K
1001001 I
1010110 V
1000001 A
J= 1001010
U=1010101
U=1010101
R=1010010
I=1001001
10001101010100101010010100101000101
b)
1001011 K
1001001 I
1010110 V
1000001 A
117
a) 4

b) se loppuu 000
b) se loppuu 000
116
a) 
b) 505
c) 1111 0110 0010
b) 505
c) 1111 0110 0010
106
a)
624:4=156
luku on jaollinen
b)
896:7=128
luku on jaollinen
c)
556:6=92, jakojäännös 4
luku ei ole jaollinen
624:4=156
luku on jaollinen
b)
896:7=128
luku on jaollinen
c)
556:6=92, jakojäännös 4
luku ei ole jaollinen
Määritelmä
Olkoot a ja n kokonaislukuja. Kokonaisluku a on jaollinen luvulla n, jos on olemassa sellainen kokonaisluku q, että a=nq
Luku a on luvun n monikerta.
Luku n on luvun a tekijä.
Jakolasku ja jakoyhtälö
Kun suoritetaan jakolasku a:n, tulokseksi saadaan osamäärä ja jakojäännös
Jakoyhtälön avulla:
Jos jakolaskun a:n osamäärä on q ja jakojäännös r, niin

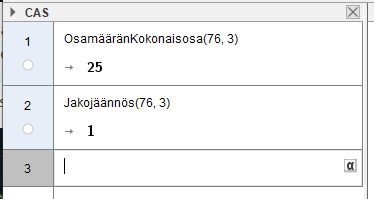
Ilmaise luku 76 muodossa
laskimella 76:3 = 25,3333...
eli

Jokainen kokonaisluku on muotoa 3q, 3q+1 tai 3q+2
Vastaavasti, kun mikä tahansa kokonaisluku jaetaan luvulla 2, jakojäännös on aina 0 tai 1
Siis jokainen kokonaisluku on näin ollen muotoa:
2q tai 2q+1
Binääri- eli kaksikantainen järjestelmä
Binäärijärjestelmässä lukujen kirjoittamiseen ei tarvita muita lukuja kuin 0 ja 1, sillä luvulla 2 jaettaessa jakojäännös on aina 0 tai 1
Esim. Kirjoitetaan binääriluku 1001011 kymmenjärjestelmän lukuna
1+2+8+64=75
Esim. Kirjoitetaan 38 binäärilukuna
Luku a on luvun n monikerta.
Luku n on luvun a tekijä.
Jakolasku ja jakoyhtälö
Kun suoritetaan jakolasku a:n, tulokseksi saadaan osamäärä ja jakojäännös
Jakoyhtälön avulla:
Jos jakolaskun a:n osamäärä on q ja jakojäännös r, niin
Ilmaise luku 76 muodossa
laskimella 76:3 = 25,3333...
eli

Jokainen kokonaisluku on muotoa 3q, 3q+1 tai 3q+2
Vastaavasti, kun mikä tahansa kokonaisluku jaetaan luvulla 2, jakojäännös on aina 0 tai 1
Siis jokainen kokonaisluku on näin ollen muotoa:
2q tai 2q+1
Binääri- eli kaksikantainen järjestelmä
Binäärijärjestelmässä lukujen kirjoittamiseen ei tarvita muita lukuja kuin 0 ja 1, sillä luvulla 2 jaettaessa jakojäännös on aina 0 tai 1
Esim. Kirjoitetaan binääriluku 1001011 kymmenjärjestelmän lukuna
1+2+8+64=75
Esim. Kirjoitetaan 38 binäärilukuna