Tehtävät
Teksti
439
a)
442
a)
b)
Kpl 4.1
401
a) 13,23
b) Pienempi
403
3.1, vähittäin 91 osaväliä


%3D-x%5E2%2B8x-7)

)
 Osavälit ovat [1,3] [3,5] [5,7].
Osavälit ovat [1,3] [3,5] [5,7].



%7B%2C%7D%5C%20f%5Cleft(4%5Cright)%5C%20ja%5C%20f%5Cleft(6%5Cright))
%2B2f%5Cleft(4%5Cright)%2B2f%5Cleft(6%5Cright)%3D38)
421
%3D-5%7B%2C%7D%5C%20f%5Cleft(2%5Cright)%3D-9%7B%2C%7D%5C%20f%5Cleft(4%5Cright)%3D-5) a) Kuvaaja on x.akselin alapuolella, joten suorakulmioiden korkeudet ovat funktion arvojen vastalukuja. Suorakulmioiden leveys on 2.
a) Kuvaaja on x.akselin alapuolella, joten suorakulmioiden korkeudet ovat funktion arvojen vastalukuja. Suorakulmioiden leveys on 2.
-f%5Cleft(2%5Cright)-f%5Cleft(4%5Cright)%5Cright)%3D2%5Cleft(5%2B9%2B5%5Cright)%3D38)
%5Capprox-A%3D-38)
dx%3D-A2%3D-2)
dx%3DA1-A2%2BA3%3D4%5Cfrac%7B1%7D%7B3%7D-2%2B%5Cfrac%7B1%7D%7B2%7D%3D2%5Cfrac%7B5%7D%7B6%7D)
%5Cright%7Cdx%3DA1%2BA2%2BA3%3D6%5Cfrac%7B5%7D%7B6%7D)
426

![A\left[0{,}\pi\right]\approx3{,}28987](https://math-demo.abitti.fi/math.svg?latex=A%5Cleft%5B0%7B%2C%7D%5Cpi%5Cright%5D%5Capprox3%7B%2C%7D28987)
![A\left[\pi{,}2\pi\right]\approx-9.67144](https://math-demo.abitti.fi/math.svg?latex=A%5Cleft%5B%5Cpi%7B%2C%7D2%5Cpi%5Cright%5D%5Capprox-9.67144)

%5Capprox2.467)

%3D)
408
411
405.
Lasketaan kuvaajan ja x-akselin leikkauskodat.
Suorakulmioita on 3 kpl eli n=3
Yhden osavälin pituus eli suorakulmion leveys on
Osavälien keskipisteet ovat
Suorakulmion korkeudet ovat fubktiob arvot välien keskpisteissä eli
b) Määrätty integraali on negatiivinen, koska kuvaaja on x-akselin alapuolella.
423
a)
b)
c)
427
3.2 Numerinen derivointi
322
a)
b)
c)
324
325
326
a)
b)
d)
329



%3D2%5E%7B-x%7D%5Ccdot%5Cleft(-%5Cln2%5Cright))
%3D2%5E%7B-1%7D%5Ccdot%5Cleft(-%5Cln2%5Cright)%3D%E2%88%920.34657...%5Capprox-0%7B%2C%7D3466)
331
%3De%5Ex)
%3De%5Ex)
%3De%5E2)
331
Raja-arvo ei ole
332
333
-f%5Cleft(a%5Cright)%7D%7Bh%7D%3D%5Cfrac%7Bf%5Cleft(0%2B%5Cleft(-0%7B%2C%7D1%5Cright)%5Cright)-f%5Cleft(0%5Cright)%7D%7B-0%7B%2C%7D1%7D%5Capprox%E2%88%921.0488)
-f%5Cleft(a%5Cright)%7D%7Bh%7D%3D%5Cfrac%7Bf%5Cleft(0%2B0%7B%2C%7D1%5Cright)-f%5Cleft(0%5Cright)%7D%7B0%7B%2C%7D1%7D%5Capprox0.9487)
-f%5Cleft(a-h%5Cright)%7D%7B2h%7D%5Capprox-0.0501)
Ei näytä oleva derivoituva
340
%5Capprox0.877586521890373)








8
3.1 Derivaatan ja derivoituvuuden tarkastelua
2.3 Kiintopistemenetelmä ja iterointi
251
a)
b)
252
C
254
257
b)
264
a)
b)
c)265
a) Funktio on kasvava eli sillä on korkeitaan yksi ratkaisu


Bolzanon lauseen nojalla voidaan oleta, että välillä ]0,2[ on ainakin yksi nollakohta.
b)
Neljäs

267
a)
272
yhdistetään funktiot, saadan funktio h(x)
Kuvan kautta voidaan ottaa 3 alkuarvausta, ja niiden avulla voidaan laskea nollakohtien x-koordnaatit
Kun x-koordinaatit on laskettu, voidaan niitä sijoita funktioon f(x) tai g(x), saadaan niiden y-koortit
Leikkauspisteet ovat
2.2 Newtonin menetelmä
229

230

231
x=1.109956 or x=3.35302 or x=5.50089
232
a)

b)

c)
ei mikään
233


234
Funktio on kasvava eli sillä on korkeitaan yksi ratkaisu%3D-2)
%3D1)
a) 3

b) 5
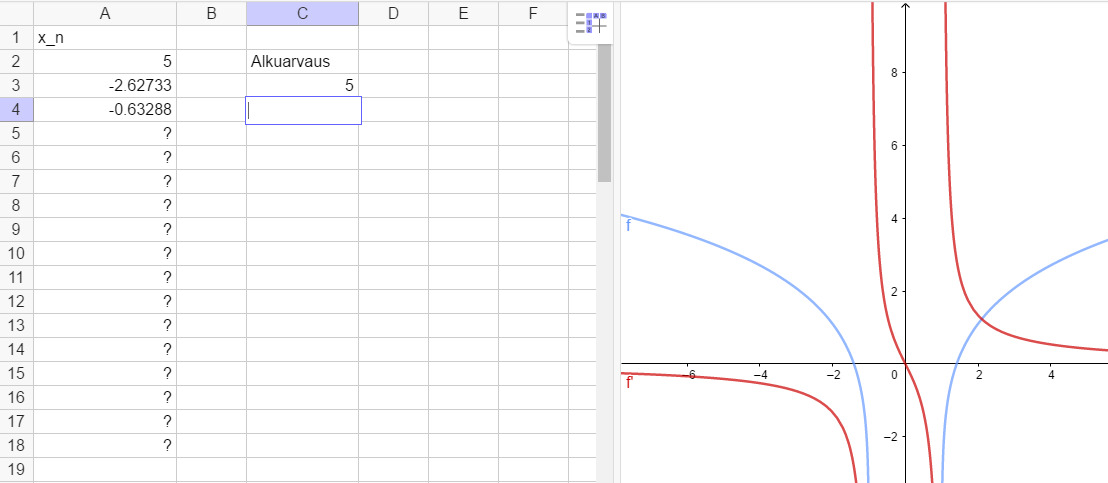
236


237
230

231
x=1.109956 or x=3.35302 or x=5.50089
232
a)
b)
c)
ei mikään
233
a)
Annettu alkuarvo ei toimi, otetaan uudeksi alkuarvoksi luku 3
b)
Annettu alkuarvo ei toimi, otetaan uudeksi alkuarvoksi luku
Funktio on kasvava eli sillä on korkeitaan yksi ratkaisu
Lasketaan funktion ratkaisut välin pätepisteessä 0 ja 1
jos tuloksien merkit vaihtuu, funktio noudataa Bolzanon lausetta, tällöin funktiolla on nollakohta avoimella välillä ]0,1[
Kun alkuarvaus1, tulos on 0,83512, ei muita ratkaisuja.
235a) 3

b) 5

236

237
Merkitään
Funktio f on jatkuva kaikkialla
Tutkitaan funktion f kulkua deravaatan avulla
Derivaattafunktio %5Cge1) , jolloin funktio f on kasvava. Siten funktiolla f voi korkeintaan olla yksi nollakohta
, jolloin funktio f on kasvava. Siten funktiolla f voi korkeintaan olla yksi nollakohta
Newtonin menetelmällä saatava likiarvo on siten funktion f ainoan nollakohdan likiarvo.
Newtonin menetelmän rekursiokaava
Käytetään alkuarvoa
Lasketaan nollakohdalle likiarvot taulukkolaskentaohjelmalla
Nollakohta 5 desimaalin tarkkuudella on 
Tarkistetaan, että näin on
Välillä ]1,063065;1,063075[ olevat luvut pyöristyvät 5 desimaalin tarkkuudella luvuksi 1,06307
238
239
yksi nollakohta
yksi nollakohta
241


242
2.1 Haarukointi ja ratkaisujen lukumäärä
201


203
%3D3x%5E2%2B3)



1,8; 1,9; 2,0
202
a)
b)
203
a)
Lasketaan funktion derivaatta nollakohdat
Ei ratkaisua
Tämä tarkoittaa sitä että funktiolla ei ole missään paikassa maksimipistettä
Lasketaan funktion nollakohdat
1.4 Polynomi yhtälön ratkaiseminen
162
Koska f(4)=0, niin olynomi on jaollinen binomilla x-4
Lasketaa jakolasku%7D%7Bx-4%7D) jakoalgoritmilla
jakoalgoritmilla
Lasketaa jakolasku
Lasketaan nollakohdat
163
Koska f(3)=0, niin olynomi on jaollinen binomilla x-3
Lasketaa jakolasku %7D%7Bx-3%7D) jakoalgoritmilla
jakoalgoritmilla
164
a) kolme
b)
a)
Nimitään %3D6x%5E3-13x%5E2%2B4%3D0)
Etsitään yhtälölle P(x)=0 jokin kokonaislukuratkaisu. Jos yhtälöllä on kokonaislukuratkaisuja, ne löydetään sijoittamalla yhtälöön vakiotermin -6 tekijöitä ±1 ±2 ±4
Etsitään yhtälölle P(x)=0 jokin kokonaislukuratkaisu. Jos yhtälöllä on kokonaislukuratkaisuja, ne löydetään sijoittamalla yhtälöön vakiotermin -6 tekijöitä ±1 ±2 ±4
Koska P(2)=0, niin olynomi on jaollinen binomilla x-2
Lasketaa jakolasku%7D%7Bx-2%7D) jakologaritmilla
jakologaritmilla
Lasketaa jakolasku
Nimitään
Jaetaan polynomi g(x) tekijöihin ryhmittelemällä.
Ratkaistaan yhtälö P(x)=0 tulon nollasäännöllä
%3D%5Cleft(3x%2B2%5Cright)%5Cleft(2x-1%5Cright))
tai



V:  ,
, .
.
b)
Nimitään %3D2x%5E4-2x%5E3-x%5E2-3x-6)
Etsitään yhtälölle P(x)=0 jokin kokonaislukuratkaisu. Jos yhtälöllä on kokonaislukuratkaisuja, ne löydetään sijoittamalla yhtälöön vakiotermin -6 tekijöitä ±1 ±2 ±3 ±6
%3D2%5Ccdot1%5E4-2%5Ccdot1%5E3-1%5E2-3%5Ccdot1-6%3D-10)
Koska P(-1)=0, niin olynomi on jaollinen binomilla x+1
Lasketaa jakolasku %7D%7Bx%2B1%7D) jakologaritmilla
jakologaritmilla
Nimitään %3D%5Cleft(2x%5E3-4x%5E2%5Cright)%2B%5Cleft(3x-6%5Cright))
Jaetaan polynomi g(x) tekijöihin ryhmittelemällä.
%3D2x%5E2%5Cleft(x-2%5Cright)%2B3%5Cleft(x-2%5Cright)%3D%5Cleft(x-2%5Cright)%5Cleft(2x%5E2%2B3%5Cright))
Ratkaistaan yhtälö P(x)=0 tulon nollasäännöllä
Jaetaan polynomi g(x) tekijöihin ryhmittelemällä.
Ei ratkaisua
V: x=0, x=-1, x=2
1.3 Polynomien jakoalgoritmi
141
%5C%5C%0A%26--------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%203x%5E2%2B16x%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(3x%5E2%2B15x%5Cright)%5C%5C%0A%26-----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20x%2B5%5C%5C%0A-%5C%20%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(x%2B5%5Cright)%5C%20%5C%5C%0A%26-------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%5C%5C%0A%26%0A%5Cend%7Barray%7D)
%5C%5C%0A%26-------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20-2x%5E2-3x%5C%5C%0A-%5C%20%5C%20%5C%20%5C%20%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(-2x%5E2%2B4x%5Cright)%5C%5C%0A%26----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20x-2%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(x-2%5Cright)%5C%5C%0A%26------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)
%5C%5C%0A%26-------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20-3x%5E3%2B8x%5E2%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(-3x%5E3%2B2x%5E2%5Cright)%5C%5C%0A%26-----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%206x%5E2-4x%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(6x%5E2-4x%5Cright)%5C%5C%0A%26--------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%202%0A%5Cend%7Barray%7D)

%3D-2%5Ccdot3%5E3%2B5%5Ccdot3%5E2%2B6%5Ccdot3-9%3D-54%2B45%2B18-9%3D-6%5Ccdot9%2B5%5Ccdot9%2B2%5Ccdot9-1%5Ccdot9%3D9%5Cleft(-6%2B5%2B2-1%5Cright)%3D0) On jaollinen
On jaollinen
%5C%5C%0A%26--------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20-x%5E2%2B6x%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(-x%5E2%2B3x%5Cright)%5C%5C%0A%26----------%5C%5C%0A%5C%20%5C%20%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%203x-9%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(3x-9%5Cright)%5C%5C%0A%26-------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)
%3D%5Cleft(x-3%5Cright)%5Cleft(-2x%5E2-x%2B3%5Cright))
%5C%5C%0A%26----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%206x%5E2%2B3x-9%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(6x%5E2%2B3x-9%5Cright)%5C%20%5C%20%5C%5C%0A%26------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)
%3D%5Cleft(x-3%5Cright)%5Cleft(-2x%5E2-x%2B3%5Cright))
%5C%5C%0A%26--------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%203x%5E2-8x%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(3x%5E2-2x%5Cright)%5C%5C%0A%26-----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20-6x%2B4%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(-6x%2B4%5Cright)%5C%20%5C%5C%0A%26-------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)
%5Cleft(x%5E2-x%2B2%5Cright))

%5Cleft(x%5E2-%5Cfrac%7B5%7D%7B3%7Dx%2B%5Cfrac%7B8%7D%7B3%7D%5Cright)%2B4)
a)
b)
c)
142
I, II, IV
143
A II
B I
C Ei mikään
D III
144
a)
b)
145
a)
b)
146
%5C%5C%0A%26--------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%204x%5E2%2B12x%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(4x%5E2%2B6x%5Cright)%5C%5C%0A%26-----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%206x%2B9%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(6x%2B9%5Cright)%5C%5C%0A%26-------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)

147
%3D2x%5E3-5x%5E2%2B3x-2)
%3D2%5Ccdot%5Cleft(-1%5Cright)%5E3-5%5Ccdot%5Cleft(-1%5Cright)%5E2%2B3%5Ccdot%5Cleft(-1%5Cright)-2%3D-2-5-3-2%3D-12)
%3D2%5Ccdot2%5E3-5%5Ccdot2%5E2%2B3%5Ccdot2-2%3D16-20%2B6-2%3D0)
%3Alla)
%5C%5C%0A%26-------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20-x%5E2%2B3x%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(-x%5E2%2B2x%5Cright)%5C%5C%0A%26----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20x-2%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(x-2%5Cright)%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%5C%0A%26------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)
%3D%5Cleft(x-2%5Cright)%5Cleft(2x%5E2-x%2B1%5Cright))
%3D6x%5E3%2B7x%5E2-1)
%3D6%5Ccdot%5Cleft(-1%5Cright)%5E3%2B7%5Ccdot%5Cleft(-1%5Cright)%5E2-1%3D-6%2B7-1%3D0)
%3D6%5Ccdot2%5E3%2B7%5Ccdot2%5E2-1%3D48%2B28-1%3D76-1%3D75)
%3All%C3%A4)
%5C%5C%0A%26-------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20x%5E2%2B0x%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(x%5E2%2Bx%5Cright)%5C%5C%0A%26---------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20-x-1%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(-x-1%5Cright)%5C%5C%0A%26-----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)
%3D2x%5E3-x%5E2%2B4x%2Bk)
%3D2%5Ccdot%5Cleft(-2%5Cright)%5E3-%5Cleft(-2%5Cright)%5E2%2B4%5Ccdot%5Cleft(-2%5Cright)%2Bk)
%5E3-%5Cleft(-2%5Cright)%5E2%2B4%5Ccdot%5Cleft(-2%5Cright)%2Bk%3D0)



%5C%5C%0A%26----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20-x%5E2%2Bk%5C%5C%0A-%5C%20%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(x%5E2%2B2%5Cright)%5C%5C%0A%26----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)

%5C%5C%0A%26------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%202x%5E2-2x%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(2x%5E2-2x%5Cright)%5C%5C%0A%26------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%201%5C%20%0A%5Cend%7Barray%7D)
%5Cleft(x%5E2%2B2%5Cright)%2B1)
%5Cleft(3x%5E2-1%5Cright)%2B2x%3D3x%5E4-x%5E2%2B3x%5E2-1%2B2x%3D3x%5E4%2B2x%5E2%2B2x-1)
 Tällöin voidaan hyödyntää hopitalin sääntöä
Tällöin voidaan hyödyntää hopitalin sääntöä
%7D%7Bg%27%5Cleft(x%5Cright)%7D%5Cright)%3D%5Cfrac%7B-6x%5E2-8x%2B18%7D%7B2%7D%3D%5Cfrac%7B-6%5Ccdot2%5E2-8%5Ccdot2%2B18%7D%7B2%7D%3D%5Cfrac%7B-24-16%2B18%7D%7B2%7D%3D-11)
%5C%5C%0A%26-------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20kx-6%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(9x-6%5Cright)%5C%5C%0A%26-----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)

%5C%5C%0A%26---------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20-x%5E2%2Bk%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(-x%5E2%2B3%5Cright)%5C%5C%0A%26-----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)

%5Ccdot%5Cleft(-2x%5E2-5x-11%5Cright)-34)
%5Ccdot%5Cleft(-2x%5E2-5x-11%5Cright))
%5C%5C%0A%26------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%206x%5E2%2B15x-33%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(6x%5E2%2B15x%2B33%5Cright)%5C%5C%0A%26--------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)
%5C%5C%0A%26--------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20-10x%5E2-28x%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(-10x%5E2-30x%5Cright)%5C%5C%0A%26------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%202x%2B6%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(2x%2B6%5Cright)%5C%5C%0A%26--------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)





%2B%5Cleft(-6x%2B2%5Cright)%3D4x%5Cleft(3x-1%5Cright)-2%5Cleft(3x-1%5Cright)%3D%5Cleft(4x-2%5Cright)%5Cleft(3x-1%5Cright))


%5C%5C%0A%26-------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20-5x%5E3-6x%5E2%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(-5x%5E3-5x%5E2%5Cright)%5C%5C%0A%26----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20-x%5E2%2B5x%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(-x%5E2-x%5Cright)%5C%5C%0A%26------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%206x%2B6%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(6x%2B6%5Cright)%5C%5C%0A%26---------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)
%5C%5C%0A%26-------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20-7x%5E2-x%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(-7x%5E2-7x%5Cright)%5C%5C%0A%26----------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%206x%2B6%5C%5C%0A-%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft(6x%2B6%5Cright)%5C%5C%0A%26------------%5C%5C%0A%26%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%200%0A%5Cend%7Barray%7D)

![x=\frac{7\pm\sqrt[]{\left(-7\right)^2-4\cdot2\cdot6}}{2\cdot2}=\frac{7\pm\sqrt[]{1}}{4}=\frac{7\pm1}{4}](https://math-demo.abitti.fi/math.svg?latex=x%3D%5Cfrac%7B7%5Cpm%5Csqrt%5B%5D%7B%5Cleft(-7%5Cright)%5E2-4%5Ccdot2%5Ccdot6%7D%7D%7B2%5Ccdot2%7D%3D%5Cfrac%7B7%5Cpm%5Csqrt%5B%5D%7B1%7D%7D%7B4%7D%3D%5Cfrac%7B7%5Cpm1%7D%7B4%7D)



%5E2%5Cleft(x-2%5Cright)%5Cleft(2x-3%5Cright))
147
a)
b)
148
a)
b)
149
150
151
152
a)
b)
153
154
155
1.2 Polymien jaollisuus
121
%7D%7Bx%2B2%7D)




%2B%5Cleft(2x%2B4%5Cright)%3Dx%5Cleft(x%2B2%5Cright)%2B2%5Cleft(x%2B2%5Cright)%3D%5Cleft(x%2B2%5Cright)%5Cleft(x%2B2%5Cright)%3D%5Cleft(x%2B2%5Cright)%5E2)
%7D%7Bx%2B2%7D%3D%5Cfrac%7B2%5Cleft(x%2B2%5Cright)%5E2%7D%7B%5Cleft(x%2B2%5Cright)%7D%3D2%5Cleft(x%2B2%5Cright)%3D2x%2B4)
%5E2%2B1%7D%7Bx%2B1%7D%3Dx%2B1%2B%5Cfrac%7B1%7D%7Bx%2B1%7D)
122
%3D3%5Ccdot1%5E2-1-2%3D3-1-2%3D0)

%2B%5Cleft(vx%2Bc%5Cright))




%2B%5Cleft(-3x-2%5Cright))
-%5Cleft(3x%2B2%5Cright)%3D%5Cleft(x-1%5Cright)%5Cleft(3x%2B2%5Cright))
%3D3%5Ccdot2%5E2-2-2%3D12-4%3D8) ei ole
ei ole
%3D3%5Ccdot1%5E2-1-2%3D0) on
on

%2B%5Cleft(vx%2Bc%5Cright))




%2B%5Cleft(-3x-2%5Cright))
-%5Cleft(3x%2B2%5Cright)%3D%5Cleft(x-1%5Cright)%5Cleft(3x%2B2%5Cright))
%5Cleft(3x%2B2%5Cright)%7D%7B2x-2%7D%3D%5Cfrac%7B%5Cleft(x-1%5Cright)%5Cleft(3x%2B2%5Cright)%7D%7B2%5Cleft(x-1%5Cright)%7D%3D%5Cfrac%7B3x%2B2%7D%7B2%7D)
%3D%5Cleft(2x-2%5Cright)%5Cleft(%5Cfrac%7B3%7D%7B2%7Dx%2B1%5Cright))
123




%2B%5Cleft(-3x%2B3%5Cright)%3D3x%5Cleft(x-1%5Cright)-3%5Cleft(x-1%5Cright)%3D%5Cleft(3x-3%5Cright)%5Cleft(x-1%5Cright)) b)
b)




%2B%5Cleft(x-4%5Cright)%3D2x%5Cleft(x-4%5Cright)%2B1%5Cleft(x-4%5Cright)%3D%5Cleft(2x%2B1%5Cright)%5Cleft(x-4%5Cright))
)
124
%5Cleft(x%2B1%5Cright)%7D%7B%5Cleft(x%2B1%5Cright)%7D%3D4%5Cleft(x-1%5Cright)%3D4x-4)
%5Cleft(x%2B1%5Cright)) b)
b)
%7D%7Bx%2B4%7D)
![x=\frac{-1\pm\sqrt[]{1^2-4\cdot1\cdot\left(-12\right)}}{2\cdot1}=\frac{-1\pm\sqrt[]{49}}{2}=\frac{-1\pm7}{2}](https://math-demo.abitti.fi/math.svg?latex=x%3D%5Cfrac%7B-1%5Cpm%5Csqrt%5B%5D%7B1%5E2-4%5Ccdot1%5Ccdot%5Cleft(-12%5Cright)%7D%7D%7B2%5Ccdot1%7D%3D%5Cfrac%7B-1%5Cpm%5Csqrt%5B%5D%7B49%7D%7D%7B2%7D%3D%5Cfrac%7B-1%5Cpm7%7D%7B2%7D)


%7D%7Bx%2B4%7D%3D%5Cfrac%7Bx%5Cleft(x-3%5Cright)%5Cleft(x%2B4%5Cright)%7D%7B%5Cleft(x%2B4%5Cright)%7D%3Dx%5Cleft(x-3%5Cright))
%5Cleft(x%2B4%5Cright))
125
a)
%3D6%5Ccdot%5Cleft(%5Cfrac%7B1%7D%7B2%7D%5Cright)%5E2-%5Cfrac%7B1%7D%7B2%7D-2%3D1%5Cfrac%7B1%7D%7B2%7D-%5Cfrac%7B1%7D%7B2%7D-2%3D-1) ei ole jaollinen
ei ole jaollinen
%3D4%5Ccdot%5Cleft(%5Cfrac%7B1%7D%7B2%7D%5Cright)%5E4-%5Cleft(%5Cfrac%7B1%7D%7B2%7D%5Cright)%5E3-%5Cfrac%7B1%7D%7B2%7D%5Ccdot%5Cleft(%5Cfrac%7B1%7D%7B2%7D%5Cright)%5E2%3D%5Cfrac%7B4%7D%7B16%7D-%5Cfrac%7B1%7D%7B8%7D-%5Cfrac%7B1%7D%7B8%7D%3D%5Cfrac%7B4%7D%7B16%7D-%5Cfrac%7B1%7D%7B4%7D%3D%5Cfrac%7B4%7D%7B16%7D-%5Cfrac%7B4%7D%7B16%7D%3D0)
%7D%3D%5Cfrac%7Bx%5E2%5Cleft(8x%5E2-2x-1%5Cright)%7D%7B2%5Cleft(2x-1%5Cright)%7D)
%3D8x%5E2-2x-1)



%2B%5Cleft(-4x-1%5Cright)%3D2x%5Cleft(4x%2B1%5Cright)-1%5Cleft(4x%2B1%5Cright)%3D%5Cleft(2x-1%5Cright)%5Cleft(4x%2B1%5Cright))
%7D%7B2%5Cleft(2x-1%5Cright)%7D%3D%5Cfrac%7Bx%5E2%5Cleft(2x-1%5Cright)%5Cleft(4x%2B1%5Cright)%7D%7B2%5Cleft(2x-1%5Cright)%7D%3D%5Cfrac%7Bx%5E2%5Cleft(4x%2B1%5Cright)%7D%7B2%7D)
%3D%5Cleft(%5Cfrac%7Bx%5E2%5Cleft(4x%2B1%5Cright)%7D%7B2%7D%5Cright)%5Ccdot%5Cleft(2x-1%5Cright))
126
%5Ccdot%5Cleft(x%2B3%5Cright))
%7D%7Bx%2B3%7D%2B%5Cfrac%7Bx%2B3%7D%7Bx%2B3%7D%2B%5Cfrac%7B3%7D%7Bx%2B3%7D%3D%5Cfrac%7Bx%5E3%2B3x%5E2%2Bx%2B6%7D%7Bx%2B3%7D)
%3D%5Cfrac%7Bx%5E3%2B3x%5E2%2Bx%2B6%7D%7Bx%2B3%7D%5Ccdot%5Cleft(x%2B3%5Cright)%3Dx%5E3%2B3x%5E2%2Bx%2B6)
%7D%7B2x-3%7D)




%2B%5Cleft(-3x%2B3%5Cright)%3D2x%5Cleft(x-1%5Cright)%2B-3%5Cleft(x-1%5Cright)%3D%5Cleft(2x-3%5Cright)%5Cleft(x-1%5Cright))
%3D%5Cfrac%7Bx%5Cleft(2x-3%5Cright)%5Cleft(x-1%5Cright)%7D%7B2x-3%7D%3Dx%5Cleft(x-1%5Cright)%3Dx%5E2-x)


%5E2%2B%5Cleft(2%5Ccdot%20b%5Ccdot3x%5Cright)%2B4%5C%20%5C%20%5C%20%5C%20%5C%20%5Cleft%7C%5Cright%7C4%3D2%5E2%7B%2C%7D%5C%20joten%5C%20b%3D%5Cpm2)
%5E2%2B%5Cleft(2%5Ccdot2%5Ccdot3x%5Cright)%2B2%5E2%3D9x%5E2%2B12x%2B4)

%2B%5Cleft(-2%5Cright)%5E2%3D%5Cleft(2x-2%5Cright)%5E2)
%5E2%3D4x%5E2%2B2%5Ccdot%5Cleft(-2%5Cright)%5Ccdot2x%2B%5Cleft(-2%5Cright)%5E2%3D4x%5E2-8x%2B4)

%7D%7Bx%5Cleft(x%2B2%5Cright)%7D%3D%5Cfrac%7Bx%5Cleft(x%2B2%5Cright)%5Cleft(x-2%5Cright)%7D%7Bx%5Cleft(x%2B2%5Cright)%7D%3Dx-2)
-4%5Cleft(x-1%5Cright)%3D%5Cleft(x%5E2-4%5Cright)%5Cleft(x-1%5Cright)%3D%5Cleft(x-2%5Cright)%5Cleft(x%2B2%5Cright)%5Cleft(x-1%5Cright)) b)
b)
%2B%5Cleft(x%2B8%5Cright)%3D%5Cleft(x%5E2%2B1%5Cright)%5Cleft(x%2B8%5Cright))
%2B2%5Cleft(x-3%5Cright)%3D%5Cleft(x%5E2%2B2%5Cright)%5Cleft(x-3%5Cright))

![x=\frac{-2\pm\sqrt[]{2^2-4\cdot2\cdot\left(-24\right)}}{2\cdot2}=\frac{-2\pm14}{4}](https://math-demo.abitti.fi/math.svg?latex=x%3D%5Cfrac%7B-2%5Cpm%5Csqrt%5B%5D%7B2%5E2-4%5Ccdot2%5Ccdot%5Cleft(-24%5Cright)%7D%7D%7B2%5Ccdot2%7D%3D%5Cfrac%7B-2%5Cpm14%7D%7B4%7D)



%3D2%5E2-2k-k%5E2-1%3D4-2k-k%5E2-1%3D-k%5E2-2k%2B3)

![k=\frac{2\pm\sqrt[]{\left(-2\right)^2-4\cdot\left(-1\right)\cdot3}}{2\cdot\left(-1\right)}=\frac{2\pm4}{-2}](https://math-demo.abitti.fi/math.svg?latex=k%3D%5Cfrac%7B2%5Cpm%5Csqrt%5B%5D%7B%5Cleft(-2%5Cright)%5E2-4%5Ccdot%5Cleft(-1%5Cright)%5Ccdot3%7D%7D%7B2%5Ccdot%5Cleft(-1%5Cright)%7D%3D%5Cfrac%7B2%5Cpm4%7D%7B-2%7D)




)

%3D2x%5E2%3D2x%5Ccdot%20x)

%3D2x%5E2%2B16x%2B32%3D2%5Cleft(x%5E2%2B8x%2B16%5Cright)%3D2%5Cleft(x%2B4%5Cright)%5E2)
-2%7D%7B2%5Cleft(x%2B2%5Cright)%7D)
-2%7D%7B2%5Cleft(x%2B2%5Cright)%7D%5Cright)%3D%5Cfrac%7B-2%5Cleft(3%5Ccdot%5Cleft(-2%5Cright)%2B5%5Cright)-2%7D%7B2%5Cleft(-2%2B2%5Cright)%7D%3D%5Cfrac%7B-2%5Cleft(-6%2B5%5Cright)-2%7D%7B2%5Ccdot0%7D%3DNollalla%5C%20jako) Käytetään Hopitalin sääntöä
Käytetään Hopitalin sääntöä
%7D%7Bg%27%5Cleft(x%5Cright)%7D%3D%5Cfrac%7B6x%2B5%7D%7B2%7D%3D%5Cfrac%7B6%5Ccdot%5Cleft(-2%5Cright)%2B5%7D%7B2%7D%3D-%5Cfrac%7B7%7D%7B2%7D)
-3%5Cleft(x-1%5Cright)%7D%7Bx-1%7D%3D%5Cfrac%7Bx%5E2%5Cleft(2%5Cleft(x-1%5Cright)%5Cright)-3%5Cleft(x-1%5Cright)%7D%7Bx-1%7D%3D%5Cfrac%7B2x%5E2%5Cleft(x-1%5Cright)-3%5Cleft(x-1%5Cright)%7D%7Bx-1%7D%3D%5Cfrac%7B%5Cleft(2x%5E2-3%5Cright)%5Cleft(x-1%5Cright)%7D%7B%5Cleft(x-1%5Cright)%7D%3D2x%5E3-3)







%2B%5Cleft(6x-3%5Cright)%3Dx%5Cleft(2x-1%5Cright)%2B3%5Cleft(2x-1%5Cright)%3D%5Cleft(x%2B3%5Cright)%5Cleft(2x-1%5Cright))
%5Cleft(2x-1%5Cright)%7D%7B3x%2Ba%7D)
%7D%7B3x%2Ba%7D%3D%5Cfrac%7Bx%2B3%7D%7B3%5Cleft(x%2B%5Cfrac%7Ba%7D%7B3%7D%5Cright)%7D)


%7D%7B3%5Cleft(x%2B%5Cfrac%7Ba%7D%7B3%7D%5Cright)%7D)

)









-4x%5E2%5Cleft(2x-1%5Cright)%3D%5Cleft(x%5E4-4x%5E2%5Cright)%5Cleft(2x-1%5Cright)%3Dx%5E2%5Cleft(x%5E2-4%5Cright)%5Cleft(2x-1%5Cright)%3Dx%5Ccdot%20x%5Cleft(x-2%5Cright)%5Cleft(x%2B2%5Cright)%5Cleft(2x-1%5Cright))
a)
b)
122
a)
On
b)
c)
123
a)
c)
124
a)
tai
125
a)
b)
126
A I
B II, IV
C II, IV
D III
127
a)
b)
128
a)
b)
c)
129
130
a)
c)
131
a)
b)
132
133
a)
b)
134
tai
135
1.1 Algoritmi
101

102
%3D0)





%3D0)













107

 b)
b)




b)
r-säteisen ja) -keskisen ympyrän yhtälö on keskipistemuodossa
-keskisen ympyrän yhtälö on keskipistemuodossa %5E2%2B%5Cleft(y-y_0%5Cright)%5E2%3Dr%5E2) . Seuraavalla algorimilla voidaan selvittää pisteen (a,b) sijaini ympyrään nähden:
. Seuraavalla algorimilla voidaan selvittää pisteen (a,b) sijaini ympyrään nähden:
1) Lasketaan luku c kaavalla%5E2%2B%5Cleft(b-y_0%5Cright)%5E2) .
.
2) Jos , niin piste on ympyrän ulkopuolella. Jos
, niin piste on ympyrän ulkopuolella. Jos  , niin piste on ympyrän sisäpuolella. Jos
, niin piste on ympyrän sisäpuolella. Jos  , niin piste on ympyrän kehällä.
, niin piste on ympyrän kehällä.



<p>
<script>
var a = 2;
var b = -1;
var c = 4;
var d = -3;
var a=2;
var b=-7;
var c=4;
var d =5;
if a*b*c*d>0:
print('numbers a b c d have the same sign')
else: {print('numbers a b c d have not the same sign')
}
</script>
a)
1)
2)
2)
b)
1)
2)
102
a)
tai
b)
tai
103
a)
b)
Jakoalgoritmissa toistetaan vaiheita
- Jaa
- Kerro
- Vähennä
- Pudota
c)
104
a)
1) Olkoon p=41. Nyt
2) 93>p, joten
3) , 11<p
, 11<p
4) Viimeisen vähennyslaskun tulos on 11
b) Algoritmilla saadaan selville jakojäännös, kun isompi luvuista jaetaan pienemmällä.
c) Algoritmi on ihmisen toteuttamana todella työläs, jos toinen luku on paljon suurempi kuin toinen.
Algoritmin ei myöskään kerro, mitä pitää tehdä, jos annetut luvut ovat yhtä suuret tai pienempi luku on nolla.
106
a)
b)
107
a) Valitaan esimerkiksi luvut a= 17 ja b= 82
110
a) Lasketaan lukujen erotus a-b. Jos erotus positiivinen, luku a on suurempi. Jos erotus ei ole positiivinen, luku b on suurempi.
b) Lasketaan lukujen erotus a-b. Jos erotus positiivinen, luku a on suurempi. Jos erotus ei ole positiivinen, lasketaan erotus b-a. Mikäli erotus on positiivinen, on luku b suurempi. Jos kumpikaan erotuksista ei ole positiivinen, niin luvut ovat keskenään yhtä suuria.
111
a)
c)
112
1) laske arvosanojen summa
2) Jakaa summa oppilaiden määrällä
113
Tulos, kun annettu luku jaetaan viidellä
114
a)
b)
Osamäärän kokonaisosa
c)
115
a)
Olkoon funktio y=f(x) kaikkialla määritelty. Seuraavalla algoritmilla, voidaan selvittää pisteen (a,b) sijainti funktioon f nähden:
Olkoon funktio y=f(x) kaikkialla määritelty. Seuraavalla algoritmilla, voidaan selvittää pisteen (a,b) sijainti funktioon f nähden:
1) Laske funktion arvo f(a).
2) Jost saatu arvo on suurempi kuin piseen y-koordinaatti eli f(a)>b, niin piste on kuvaajan alapuolella. Jos f(a)<b, niin piste on kuvaajan yläpuolella. Jos f(a)=b, niin piste on kuvaajalla.
b)
r-säteisen ja
1) Lasketaan luku c kaavalla
2) Jos
116
a)
b)
Murtolukujen osamäärä
c)
Helppo käyttää
117
Itse ohjelma:<p>
<script>
var a = 2;
var b = -1;
var c = 4;
var d = -3;
var a=2;
var b=-7;
var c=4;
var d =5;
if a*b*c*d>0:
print('numbers a b c d have the same sign')
else: {print('numbers a b c d have not the same sign')
}
</script>





