Kotitehtävät
Tehtävät 14 S.127
14-2
a) Yksi miljardeista galakseista, jolal aurinkokuntamme sijaitsee.
b) Se muodosruu tähtistä ja tähden kiertolaisista, kaasusta ja pölystä.
c) Galaksijoukoksi kutsutaan semmoista joukkoa, jossa on kymmenittäin galakseja pienellä alueella.
d) Pienempi kuin paneetta, mutta suurempi kuin mereori ja on kivinen kappale.
e) Komeetta muistutta asteroidia ja koostuu jäästä. Se on pienei auringon kappale.
f) Tähdenlento on puhekielessä käytetty ilmaisu meteorille, joka palaa ilmakehässä.
14-3
a) Tähti on kaasua, joka pakkautunut palloksi ja planeetta tähteä kiertävä kappale.
b) Meteoriitti on maahan tai muun kappaleen päälle pudonnut kivi ja meteoridi on ilmakehässä palava kivi eli toinen on lentävä ja toinen on jo maahan pudonnut.
c) Planeetta sijaitsee meidän aurinkokunnassa ja eksoplaneetta ei.
a) Yksi miljardeista galakseista, jolal aurinkokuntamme sijaitsee.
b) Se muodosruu tähtistä ja tähden kiertolaisista, kaasusta ja pölystä.
c) Galaksijoukoksi kutsutaan semmoista joukkoa, jossa on kymmenittäin galakseja pienellä alueella.
d) Pienempi kuin paneetta, mutta suurempi kuin mereori ja on kivinen kappale.
e) Komeetta muistutta asteroidia ja koostuu jäästä. Se on pienei auringon kappale.
f) Tähdenlento on puhekielessä käytetty ilmaisu meteorille, joka palaa ilmakehässä.
14-3
a) Tähti on kaasua, joka pakkautunut palloksi ja planeetta tähteä kiertävä kappale.
b) Meteoriitti on maahan tai muun kappaleen päälle pudonnut kivi ja meteoridi on ilmakehässä palava kivi eli toinen on lentävä ja toinen on jo maahan pudonnut.
c) Planeetta sijaitsee meidän aurinkokunnassa ja eksoplaneetta ei.
Tehtävät 13 S.119
13-2
- Kosminen taustasäteily.
- Galaksie loittoneminen.
13-5
a) Totta
b) Totta
c) Vääri, laajeneminen on kiihtyvää.
d) Väärin, ensimmäiset atomit syntyivät vasta 400 000 vuotta sitten.
e) Väärin
- Kosminen taustasäteily.
- Galaksie loittoneminen.
13-5
a) Totta
b) Totta
c) Vääri, laajeneminen on kiihtyvää.
d) Väärin, ensimmäiset atomit syntyivät vasta 400 000 vuotta sitten.
e) Väärin
Tehtävät 15 S.132
15-1
Pitävätkö seuraavay väitteet paikkansa?
a) Atomin ydin muodostuu protoneista ja elektroneista.
Ei
b) Atomi muodostuu elektroneista, u-kvarkeista ja d-kvarkeista.
Kyllä
c) Ytimen ja elektroniverhon välillä on sähkömagneettinen vuorovaikutus.
Kyllä
d) Luonnossa tiedetään olevan kuusi rilaista kvarkkilajia.
Kyllä
e) Elektroni koostuu kvarkeista.
Ei
f) Kvarkeilal ei ole sähkövarausta.
Ei
15-6
a) Luettele kvarkit
Kvarkit: u(up), c (charm), t (truth tai top), d (down), s (strange), b (beauty tai bottom)
b) Mistä kvarkeista näkyvä aine koostuu?
u:sta ja d:sta
c) Mitkä ovat perushiukkaset?
Kvarkit ja leptonit
Pitävätkö seuraavay väitteet paikkansa?
a) Atomin ydin muodostuu protoneista ja elektroneista.
Ei
b) Atomi muodostuu elektroneista, u-kvarkeista ja d-kvarkeista.
Kyllä
c) Ytimen ja elektroniverhon välillä on sähkömagneettinen vuorovaikutus.
Kyllä
d) Luonnossa tiedetään olevan kuusi rilaista kvarkkilajia.
Kyllä
e) Elektroni koostuu kvarkeista.
Ei
f) Kvarkeilal ei ole sähkövarausta.
Ei
15-6
a) Luettele kvarkit
Kvarkit: u(up), c (charm), t (truth tai top), d (down), s (strange), b (beauty tai bottom)
b) Mistä kvarkeista näkyvä aine koostuu?
u:sta ja d:sta
c) Mitkä ovat perushiukkaset?
Kvarkit ja leptonit
Tehtävät 12 S.113
12-1
Luettele perusvuorovaikutukset niiden voimakkuuden mukaisessa järjestyksessä
Vahva vuorovaikutus
Sähkömagneettinen vuorovaikutus
Heikko vuorovaikutus
Gravitaatiovuorovaikutus
12-3
Mikä perusvuorovaikutus on vallitseva seuraavissa tapauksissa:
a) Lumi putoaa katolta
- Gravitaatiovuorovaikutus
b) Rikkiatomin yhdin pysyy koossa
- Vahva vuorovaikutus
c) Ohut kääremuovi takertuu sormiin
- Sähkömagneettinen vuorovaikutus
d) Korvanappikuulokkeet hylkivät toisiaan
- Sähkömagneettinen vuorovaikutus
e) Cesiumydin säteilee elektroneja
- Heikko vuorovaikutus
12-4
Arvio seuraavien väitteiden paikkansapitävyyttä:
a) Gravitaatio vaikuttaa vain taivaankappaleiden välillä.
- Epätosi
b) Sähköien voima ja magneettinen voima liittyvät samaan perusvuorovaikutukseen.
- Tosi
c) Lattian jalkapohjisi kohdistama voima aiheutuu gravitaatiovuorovaikuksesta.
- Epätosi
d) Ainoa vuorovaikutus ytimessä on vahava vuorovaikutus.
- Epätosi
e) Sähköinen magneettinen vuorovaikutus määrää aineen kemialliset ominaisuudet.
- Tosi
f) Vahva vuorovaikutus sitoo kvarkit toisiinsa.
- Tosi
g) Beeta-aktiivisuus aiheutuu heikosta vuorovaikutuksesta.
- Tosi
Luettele perusvuorovaikutukset niiden voimakkuuden mukaisessa järjestyksessä
Vahva vuorovaikutus
Sähkömagneettinen vuorovaikutus
Heikko vuorovaikutus
Gravitaatiovuorovaikutus
12-3
Mikä perusvuorovaikutus on vallitseva seuraavissa tapauksissa:
a) Lumi putoaa katolta
- Gravitaatiovuorovaikutus
b) Rikkiatomin yhdin pysyy koossa
- Vahva vuorovaikutus
c) Ohut kääremuovi takertuu sormiin
- Sähkömagneettinen vuorovaikutus
d) Korvanappikuulokkeet hylkivät toisiaan
- Sähkömagneettinen vuorovaikutus
e) Cesiumydin säteilee elektroneja
- Heikko vuorovaikutus
12-4
Arvio seuraavien väitteiden paikkansapitävyyttä:
a) Gravitaatio vaikuttaa vain taivaankappaleiden välillä.
- Epätosi
b) Sähköien voima ja magneettinen voima liittyvät samaan perusvuorovaikutukseen.
- Tosi
c) Lattian jalkapohjisi kohdistama voima aiheutuu gravitaatiovuorovaikuksesta.
- Epätosi
d) Ainoa vuorovaikutus ytimessä on vahava vuorovaikutus.
- Epätosi
e) Sähköinen magneettinen vuorovaikutus määrää aineen kemialliset ominaisuudet.
- Tosi
f) Vahva vuorovaikutus sitoo kvarkit toisiinsa.
- Tosi
g) Beeta-aktiivisuus aiheutuu heikosta vuorovaikutuksesta.
- Tosi
Tehtävät S.101
11-2
Luettele urheilulajeja, joissa kitkaa tai väliaineen vastusta pyritään
a) Hyödyntämään
- Moottoriurheilu
b) Vähentämään
- Talviurheilu (Luistelu, laskettelu, jääkiekko)
11-3
Mainitse kaksi tilannetta, joissa kitka on kappaleen liikettä
a) Vastustava voima
- Polkupyörän jarruttaminen
b) Ylläpitävä tai kiihdyttävä voima
- Eteepäin kulkevan auton liike
11-4
Kappaleen kohdistuvaa liukukirtkaa tutkittiin vetämällä kappaletta vaakasuoraa pintaa pitkin. Kappaleen nopeus oli vakio. Tulokset ovat taulukossa.
a) Laske liukukitka virherajoineen, Arvioi virhettä vaihteluvälin puolikkaan avulla.

b) Miksi mitatut voiman arvot poikkeavat hieman toisistaan?
- Koska kappaleeseen kohdistuva voima eri ajalla ei voi olla täysin saman suuruisia.
c) Miksi mittauksen alun arvoja ei ole otettu mukaan, vaan arvot alkavat hetkellä 3,0s?
- Koska halutaan niin, että nopeus pysyy vakiona.
11-6
Ovatko seuraavat väitteet oikein?
a) Ilmanvastus kasvaa, kun kappaleen nopeus kasvaa.
-Oikein
b) Vierimisvastus aiheuttaa auton renkaiden lämpenemistä ajon aikana.
-Oikein
11-7
Oheinen kuvaaja esittää auton jarrujen testauksessa mitattua auton kiihtyvyyttä.
a) Mitä kiihtyvyyden negatiivinen arvo tarkoittaa?
- Liike on hidastuvaa
b) Kuinka suuri on auton kiihtyvyys voimakkaimman jarrutuksen aikana?
- -7,2 m/s2
c) Mitkä voimat aiheuttavat negatiivisen kiihtyvyyden?
- Kitka, ilmavastus
d) Laske edellä määritettyä kiihtyvyyttä vastaava jarruttavan voiman suuruus, kun auton kokonaismassa kuljettajineen on 1485 kg.

Luettele urheilulajeja, joissa kitkaa tai väliaineen vastusta pyritään
a) Hyödyntämään
- Moottoriurheilu
b) Vähentämään
- Talviurheilu (Luistelu, laskettelu, jääkiekko)
11-3
Mainitse kaksi tilannetta, joissa kitka on kappaleen liikettä
a) Vastustava voima
- Polkupyörän jarruttaminen
b) Ylläpitävä tai kiihdyttävä voima
- Eteepäin kulkevan auton liike
11-4
Kappaleen kohdistuvaa liukukirtkaa tutkittiin vetämällä kappaletta vaakasuoraa pintaa pitkin. Kappaleen nopeus oli vakio. Tulokset ovat taulukossa.
| t (s) | 3,0 | 3,5 | 4,0 | 4.5 | 5.0 |
| F (N) | 2,71 | 2,52 | 2,67 | 2,59 | 2,66 |
| t (s) | 5,5 | 6,0 | 6,5 | 7,0 | 7,5 |
| F (N) | 2,70 | 2,69 | 2,64 | 2,60 | 2,68 |
b) Miksi mitatut voiman arvot poikkeavat hieman toisistaan?
- Koska kappaleeseen kohdistuva voima eri ajalla ei voi olla täysin saman suuruisia.
c) Miksi mittauksen alun arvoja ei ole otettu mukaan, vaan arvot alkavat hetkellä 3,0s?
- Koska halutaan niin, että nopeus pysyy vakiona.
11-6
Ovatko seuraavat väitteet oikein?
a) Ilmanvastus kasvaa, kun kappaleen nopeus kasvaa.
-Oikein
b) Vierimisvastus aiheuttaa auton renkaiden lämpenemistä ajon aikana.
-Oikein
11-7
Oheinen kuvaaja esittää auton jarrujen testauksessa mitattua auton kiihtyvyyttä.
a) Mitä kiihtyvyyden negatiivinen arvo tarkoittaa?
- Liike on hidastuvaa
b) Kuinka suuri on auton kiihtyvyys voimakkaimman jarrutuksen aikana?
- -7,2 m/s2
c) Mitkä voimat aiheuttavat negatiivisen kiihtyvyyden?
- Kitka, ilmavastus
d) Laske edellä määritettyä kiihtyvyyttä vastaava jarruttavan voiman suuruus, kun auton kokonaismassa kuljettajineen on 1485 kg.
Tehtävät S.95
10-1
a) Miksi auto takaikkunan hyllyllä olevat irtonaiset esineet ovat turvallisuusriski liikenteessä.
- Kun auto pysähtyy nopeasti esimerkiksi törmätessään esteeseen, irtonaiset tavarat sinkoutuvat kohti tuulilasia, samoin matkustaja, joka ei ole kiinnittänyt turvavyötä.
b) Miten auton sisällä katosta riippuva nallekarhu reagoi, kun autoa jarrutetaan, kiihdytetään tai auton nopeus pysyy vakiona?
- Jarrutaessa: Lähtee lentämään kohti tuulilasia.
- Kiihdytäessä: Kaalistu taka tuulilasia päin.
- Pysähtynyt: Pysyy paikallaan.
c) Miten saat kauhaan tarttuneen muusin tipahtamaan lautaselle?
- Heitelemällä sitä kauhaa. Heiteleessä muusi jatkaa matkaa, ja tipuu lautaselle.
d) Miksi pääntuet ovat hyödyllisiä autojen istuimissa?
- Koska kun auto kiihtyy, se tukee meidän kaulaa ja päätä.
10-3
Kuvassa on esitetty moukarin rata ennen heittoa vastapäivään ylhäältä päin katsottuna. Moukari irtoaa pisteessä A. Mikä viivoista 1, 2, 3 tai 4 kuvaa moukarin lentorataa irtoamisen jälkeen.
- 2
10-5
Mitä voima kohdistuu
a) Pöydällä olevaan kukkamaljakkoon
- Painovoima, tukivoima
b) Naulakon koukkuun ripustettuun takkiin
- Painovoima, tukivoima(Jännitysvoima)
c) Maata kohti vakionopeudella leijuvaan lumihiutaleeseen?
- Painovoima, ilmavastus
10-6
Kynttilä on pöydällä ja kaappia töynnetään lattiaa pitkin vakionopeudella. Täydenä voimakuvioihin puuttuvat voimat.
a)Tukivoima
b) Painovoima , Kitka
, Kitka  , Kiihtyvys(vakio)
, Kiihtyvys(vakio)
10-8
Laatikkoa vedettiin pitkin vaakasuoraa lattiaa. Laatikon nopeus oli vakio. Vetävän voima suuruus taulukoitiin puolen sekunnin välein.
a) Esitä graafisesti voima ajan funktiona.
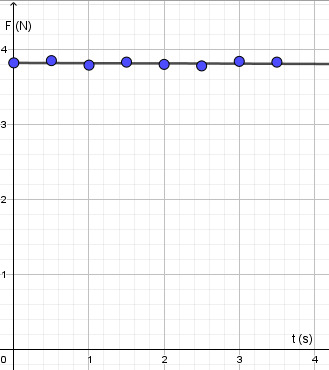
b) Piirrä laatikon voima kuvio, kun laatikon paino on 7,6 N. Kuinka suuri on kitka?

3.8 N
a) Miksi auto takaikkunan hyllyllä olevat irtonaiset esineet ovat turvallisuusriski liikenteessä.
- Kun auto pysähtyy nopeasti esimerkiksi törmätessään esteeseen, irtonaiset tavarat sinkoutuvat kohti tuulilasia, samoin matkustaja, joka ei ole kiinnittänyt turvavyötä.
b) Miten auton sisällä katosta riippuva nallekarhu reagoi, kun autoa jarrutetaan, kiihdytetään tai auton nopeus pysyy vakiona?
- Jarrutaessa: Lähtee lentämään kohti tuulilasia.
- Kiihdytäessä: Kaalistu taka tuulilasia päin.
- Pysähtynyt: Pysyy paikallaan.
c) Miten saat kauhaan tarttuneen muusin tipahtamaan lautaselle?
- Heitelemällä sitä kauhaa. Heiteleessä muusi jatkaa matkaa, ja tipuu lautaselle.
d) Miksi pääntuet ovat hyödyllisiä autojen istuimissa?
- Koska kun auto kiihtyy, se tukee meidän kaulaa ja päätä.
10-3
Kuvassa on esitetty moukarin rata ennen heittoa vastapäivään ylhäältä päin katsottuna. Moukari irtoaa pisteessä A. Mikä viivoista 1, 2, 3 tai 4 kuvaa moukarin lentorataa irtoamisen jälkeen.
- 2
10-5
Mitä voima kohdistuu
a) Pöydällä olevaan kukkamaljakkoon
- Painovoima, tukivoima
b) Naulakon koukkuun ripustettuun takkiin
- Painovoima, tukivoima(Jännitysvoima)
c) Maata kohti vakionopeudella leijuvaan lumihiutaleeseen?
- Painovoima, ilmavastus
10-6
Kynttilä on pöydällä ja kaappia töynnetään lattiaa pitkin vakionopeudella. Täydenä voimakuvioihin puuttuvat voimat.
a)Tukivoima
b) Painovoima
10-8
Laatikkoa vedettiin pitkin vaakasuoraa lattiaa. Laatikon nopeus oli vakio. Vetävän voima suuruus taulukoitiin puolen sekunnin välein.
| t(s) | 0,0 | 0,5 | 1,0 | 1,5 |
| F(N) | 3,82 | 3,85 | 3,79 | 3,83 |
| t(s) | 2,0 | 2,5 | 3,0 | 3,5 |
| F(N) | 3,80 | 3,78 | 3,84 | 3,83 |

b) Piirrä laatikon voima kuvio, kun laatikon paino on 7,6 N. Kuinka suuri on kitka?

3.8 N
S. 89 Tehtävät
9-1
Kappaleeseen vaikuttaa nollasta eroava kokonaisvoima, joka on vakio. Mitkä seuraavista väitteistä ovat tosia?
a) Kappale on tasaisessa liikkeessä.
- Epätosi
b) Kappale on tasaisesti kiihtyvässä liikkeessä
- Tosi
c) Kappaleen nopeus on vakio
- Epätosi
d) Kappaleen kiihtyvyys on vakio.
- Tosi
9-4
Avaruuslennolle Marsiin lähtevän astronautin massaksi mitataan lähdettävässä 92 kg. Astronauttiin kohdistuva paino Marsissa on
a) 92 kg
b) 900 N
c) 340 N

V: c
9-6
Pikajuoksijan massa on 88 kg. Kuinka suuri on häneen kohdistuva kokonaisvoima sillä hetkellä, kun kiihtyvyys on 3,2m/s2?

9-7
Tarkastellaan kiihtyvässä liikkeessä olevia kappaleita.
a) Laske kappaleeseen vaikuttava voima, kun kappaleen massa on 420 g ja kiihtyvyys 4,7m/s2?

b) Laske kappaleen kiihtyvyys, kun kappaleen massa on 12 t ja kappaleeseen vaikuttava voima 0,98kN.



9-9
Herkkäliikkeisen vaunun liikkeen muutosta mitattiin vaunuradalla samanaikaisesti liikeanturilla ja vaunuun kohdistuvaa voimaa voima-anturilla. Liikeanturin avulla saatiin vaunun nopeudeksi taulukon mukaiset arvot.
a) Määritä vaunun kiihtyvyys liikkeen kuvaajasta.

b) Oheisessa kuvassa on esitetty vaunuun kohdistuvan voiman suuruus kiihdytyksen aikana. Määritä vaunun massa.

Kappaleeseen vaikuttaa nollasta eroava kokonaisvoima, joka on vakio. Mitkä seuraavista väitteistä ovat tosia?
a) Kappale on tasaisessa liikkeessä.
- Epätosi
b) Kappale on tasaisesti kiihtyvässä liikkeessä
- Tosi
c) Kappaleen nopeus on vakio
- Epätosi
d) Kappaleen kiihtyvyys on vakio.
- Tosi
9-4
Avaruuslennolle Marsiin lähtevän astronautin massaksi mitataan lähdettävässä 92 kg. Astronauttiin kohdistuva paino Marsissa on
a) 92 kg
b) 900 N
c) 340 N
V: c
9-6
Pikajuoksijan massa on 88 kg. Kuinka suuri on häneen kohdistuva kokonaisvoima sillä hetkellä, kun kiihtyvyys on 3,2m/s2?
9-7
Tarkastellaan kiihtyvässä liikkeessä olevia kappaleita.
a) Laske kappaleeseen vaikuttava voima, kun kappaleen massa on 420 g ja kiihtyvyys 4,7m/s2?
b) Laske kappaleen kiihtyvyys, kun kappaleen massa on 12 t ja kappaleeseen vaikuttava voima 0,98kN.
9-9
Herkkäliikkeisen vaunun liikkeen muutosta mitattiin vaunuradalla samanaikaisesti liikeanturilla ja vaunuun kohdistuvaa voimaa voima-anturilla. Liikeanturin avulla saatiin vaunun nopeudeksi taulukon mukaiset arvot.
| t (s) | v (m/s) |
| 0,00 | 0,00 |
| 0,50 | 0,40 |
| 1,00 | 0,76 |
| 1,50 | 1,18 |
| 2,00 | 1,54 |
b) Oheisessa kuvassa on esitetty vaunuun kohdistuvan voiman suuruus kiihdytyksen aikana. Määritä vaunun massa.
S. 68-69 Tehtävät
7-2
Herkkäliikkeisen vaunun liikettä kaltevalla tasolla tutkittiin liikeanturin avulla. Kuvassa on vaunun nopeuden kuvaaja.
a) Kuvaile vaunun liikettä. Mikä oli mittauksen alkaessa vauun nopeus.
- 0,25 m/s
b) Määritä vaunun kiihtyvyys.

7-4
Polkupyöräilijä ajaa 10,0 sekuntia vakionopeudella 3,0m/s. Tämän jälkeen hän tulee alamäkeen, jossa 4,0 sekunnin ajan nopeutta tulee joka sekunti 2,0m/s lisää. Alamäen päätyttyä ajo jatkuu saavutetulla vakionopeudella. Piirrä pyöräilijän liikettä esittävä kuvaa ja t,v-koordinaatistoon.

7-7
Pekka lähtee liikennevaloista moottoripyörällään vakiokiihtyvyydellä 4,1 m/s. Pyörän nopeus 3,0 sekunnin kuluttua lähdöstä on
a) 44 km/h
b) 12 m/s
c) 1,4 m/s

7 -10
Kun ilmassa putoavan kappaleen nopeus mitattiin, saattiin seuraavat tulokset:
a) Piirrä kappaleen nopeuden kuvaaja v=v (t).
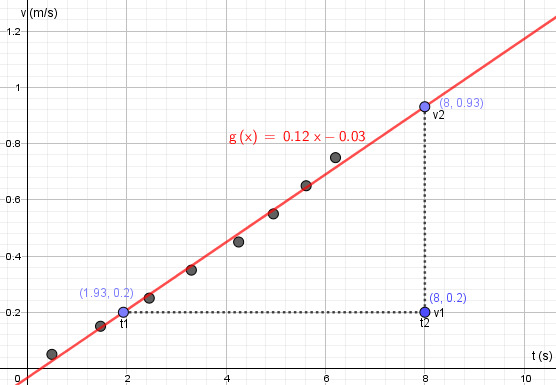
b) Perustele kuvaajan muoto.
Kysessä oleva liike on putoaminen, joka on myös kiihtyväliike. Tässä topeus kiihtyy koko ajan, ja siksi kuvaaja on myös nouseva.
7-11
Formula 1-auto törmää rengasvaliin nopeudella 130 km/h ja pysähti 0,14 sekunnissa. Laske auton ja kuljettajan kiihtyvyys törmäyksessä. Oletetaan liike tasaisesti hidastuvaksi.


Kyseessä on hidastuminen, joten liikkeen kiihtyvys on oltava negatiivinen.

tai


Herkkäliikkeisen vaunun liikettä kaltevalla tasolla tutkittiin liikeanturin avulla. Kuvassa on vaunun nopeuden kuvaaja.
a) Kuvaile vaunun liikettä. Mikä oli mittauksen alkaessa vauun nopeus.
- 0,25 m/s
b) Määritä vaunun kiihtyvyys.
7-4
Polkupyöräilijä ajaa 10,0 sekuntia vakionopeudella 3,0m/s. Tämän jälkeen hän tulee alamäkeen, jossa 4,0 sekunnin ajan nopeutta tulee joka sekunti 2,0m/s lisää. Alamäen päätyttyä ajo jatkuu saavutetulla vakionopeudella. Piirrä pyöräilijän liikettä esittävä kuvaa ja t,v-koordinaatistoon.

7-7
Pekka lähtee liikennevaloista moottoripyörällään vakiokiihtyvyydellä 4,1 m/s. Pyörän nopeus 3,0 sekunnin kuluttua lähdöstä on
a) 44 km/h
b) 12 m/s
c) 1,4 m/s
a)
v: a ja b.
v: a ja b.
7 -10
Kun ilmassa putoavan kappaleen nopeus mitattiin, saattiin seuraavat tulokset:
| t (s) | 0,05 | 0,15 | 0,25 | 0,35 | 0,45 | 0,55 | 0,65 | 0,75 |
| v (m/s) | 0,49 | 1,47 | 2,45 | 3,30 | 4,25 | 4,95 | 5,61 | 6,20 |

b) Perustele kuvaajan muoto.
Kysessä oleva liike on putoaminen, joka on myös kiihtyväliike. Tässä topeus kiihtyy koko ajan, ja siksi kuvaaja on myös nouseva.
7-11
Formula 1-auto törmää rengasvaliin nopeudella 130 km/h ja pysähti 0,14 sekunnissa. Laske auton ja kuljettajan kiihtyvyys törmäyksessä. Oletetaan liike tasaisesti hidastuvaksi.
Kyseessä on hidastuminen, joten liikkeen kiihtyvys on oltava negatiivinen.
tai
S. 60-61 Tehtävät
6-2
Kuvaaja esittää kappaleien A ja B paikka ajan funktiona.
a) Onko kappaleiden A ja B liike tasaista? Perustele.
- On, koska kuvaajan kasvu on tasainen, eli kun aika muuttuu, matka tulee samalla lisää.
b) Kuman nopeus on suurempi? Perustele.
- A, koska sen kuvaaja on yrkämpi
6-3
Kuvassa on kappaleiden A ja B paikan kuvaajat.
a) Milloin kappaleet kohtaavat?
- 2,0s
b) Määritä nopeammin kulkevan kappaleen nopeus.
A:

B:

c) Piirrä nopeammin kulkevan kappaleen nopeuden kuvaaja.
-
6-6
Autoilijan reaktioajala tarkoitetaan aikaan ,joka kuluu esteen havaitsemista jarrutuksen aloittamiseen. Reaktioaika on yleensä noin 1 sekunti. Kuinka pitkän matkan auto kulkee reaktioaikana, kun kerkivauhti on 120km/h.

6-9
Sinivalaan matala ääni voi edetä syvällä meressä satoja kilometrejä. Äänen nopeus näissä olosuhteissa on noin 1440m/s. Kuinka pitkä aika kuluu, kun sinivalaan ääni etenee 550km.
-

6-16
Taloudellisuusajokilpailuun osallistuvalla moottori pyörllä ajettiin puolet 126 kilometrin tarkkailumatkasta keskivauhdilla 95km/h ja puolet keskivauhdilla 75km/h. Mikä oli moottooripyörän keskivauhtitarkkailumatkalle.



)



Kuvaaja esittää kappaleien A ja B paikka ajan funktiona.
a) Onko kappaleiden A ja B liike tasaista? Perustele.
- On, koska kuvaajan kasvu on tasainen, eli kun aika muuttuu, matka tulee samalla lisää.
b) Kuman nopeus on suurempi? Perustele.
- A, koska sen kuvaaja on yrkämpi
6-3
Kuvassa on kappaleiden A ja B paikan kuvaajat.
a) Milloin kappaleet kohtaavat?
- 2,0s
b) Määritä nopeammin kulkevan kappaleen nopeus.
A:
B:
c) Piirrä nopeammin kulkevan kappaleen nopeuden kuvaaja.
-

6-6
Autoilijan reaktioajala tarkoitetaan aikaan ,joka kuluu esteen havaitsemista jarrutuksen aloittamiseen. Reaktioaika on yleensä noin 1 sekunti. Kuinka pitkän matkan auto kulkee reaktioaikana, kun kerkivauhti on 120km/h.
6-9
Sinivalaan matala ääni voi edetä syvällä meressä satoja kilometrejä. Äänen nopeus näissä olosuhteissa on noin 1440m/s. Kuinka pitkä aika kuluu, kun sinivalaan ääni etenee 550km.
-
6-16
Taloudellisuusajokilpailuun osallistuvalla moottori pyörllä ajettiin puolet 126 kilometrin tarkkailumatkasta keskivauhdilla 95km/h ja puolet keskivauhdilla 75km/h. Mikä oli moottooripyörän keskivauhtitarkkailumatkalle.
S.33 Tehtävät
3-3
Ilmoita suureen arvo käyttäen 1) kymmenen potenssia ja 2) sopivaa etuliitettä:
a) juoksumatkan pituus
b) mikroprosessorin taajuus
c) kalvon paksuus
d) Hiuksen paksuus
3-5
Kirjoita suureen arvo ilman etuliitettä ja kymmenen potenssia:
a) kiintolevyn kapasiteetti
b) kännykkätaajuus
c) sinisen valon aallonpituus
3-6
a) Betonilaatan pituus on 35cm ja leveys 35 cm. Ilmoita laatan pinta-ala neliömetreinä.


b) Tiilistä muuratun laatikon tilavuus on . Kuinka monta litraa vettä laatikkoon mahtuu?
. Kuinka monta litraa vettä laatikkoon mahtuu?


c) Kiven tilavuus on . Ilmoita tilavuus kuutiometreinä.
. Ilmoita tilavuus kuutiometreinä.

3-7
a) Ilmoita ihmisen päivittäinen energiantarve 2100 kcal käyttäen yksikköä megajoule (MJ).



b) Muunna teho 83 hv kilowateiksi.



3-9
a) Ilmoita 24 m/s käyttäen yksikköä km/h.



b) Ilmoita 120 km/h käyttäen yksikköä m/s.


 c) Ilmoita 100 km/h käyttäen yksikköä mailia/tunti (mph).
c) Ilmoita 100 km/h käyttäen yksikköä mailia/tunti (mph).



d) Veneilyssä solmu tarkoittaa meripeninkulmaa tunnissa. Ilmoita 22 solmua käyttäen yksikköä km/h.



3-10
Ilmoita
a) 5,25h tunteina ja minuutteina

b) 2h 45 min desimaalilukuna

Ilmoita suureen arvo käyttäen 1) kymmenen potenssia ja 2) sopivaa etuliitettä:
a) juoksumatkan pituus
b) mikroprosessorin taajuus
c) kalvon paksuus
d) Hiuksen paksuus
3-5
Kirjoita suureen arvo ilman etuliitettä ja kymmenen potenssia:
a) kiintolevyn kapasiteetti
b) kännykkätaajuus
c) sinisen valon aallonpituus
3-6
a) Betonilaatan pituus on 35cm ja leveys 35 cm. Ilmoita laatan pinta-ala neliömetreinä.
b) Tiilistä muuratun laatikon tilavuus on
c) Kiven tilavuus on
3-7
a) Ilmoita ihmisen päivittäinen energiantarve 2100 kcal käyttäen yksikköä megajoule (MJ).
b) Muunna teho 83 hv kilowateiksi.
3-9
a) Ilmoita 24 m/s käyttäen yksikköä km/h.
b) Ilmoita 120 km/h käyttäen yksikköä m/s.
d) Veneilyssä solmu tarkoittaa meripeninkulmaa tunnissa. Ilmoita 22 solmua käyttäen yksikköä km/h.
3-10
Ilmoita
a) 5,25h tunteina ja minuutteina
b) 2h 45 min desimaalilukuna
S.25 Tehtävät
2-5
Kuinka monta merkitsevää numeroa on mittaustuloksessa
a) 13s, 2
b) 15,0kg, 3
c) 0,2m 1
d) 0,047g 2
e) 400m 1,2 tai 3
2-6
Paistipalan massaksi mitattiin puolitoista kilogrammaa yhden gramman tarkkuudella. Kumpi punnistustulos on ilmoitettu oikein, 1500 g vai 1,500 kg? Perustele vastauksesi.
- 1,500 kg, koska puolistoista kilo ei ole tarkka arvo, vaan se on pyöristetty arvo. Kaikki ne, joita on pienempi kuin 1,54 tai suurempi kuin 1,44 pyöristyy 1,5 kiloon.
2-7
Opiskelijat pudottivat tennispallon 25 metriä korkean hyppyrin lähtotasanteelta. Ajat mitattiin matkapuhelimen ajanottolaitteella.
a)Ilmoita putoamisaika virherajoineen. Käytä virheen keskipoikkeamaa.

b) Laske ajan suhteellinen virhe.

c) Mitä virhelähteitä mittaukseen liittyy? Miten mittauksen voisi tehdä tarkemmaksi?
- Mittajien määrä, mittaukset ja pokkeamat.
Mitä enemmän mittajia on, sitä enemmän mittauksia saadaan, ja sitä tarkemmin mittauksesta tulee.
Kuinka monta merkitsevää numeroa on mittaustuloksessa
a) 13s, 2
b) 15,0kg, 3
c) 0,2m 1
d) 0,047g 2
e) 400m 1,2 tai 3
2-6
Paistipalan massaksi mitattiin puolitoista kilogrammaa yhden gramman tarkkuudella. Kumpi punnistustulos on ilmoitettu oikein, 1500 g vai 1,500 kg? Perustele vastauksesi.
- 1,500 kg, koska puolistoista kilo ei ole tarkka arvo, vaan se on pyöristetty arvo. Kaikki ne, joita on pienempi kuin 1,54 tai suurempi kuin 1,44 pyöristyy 1,5 kiloon.
2-7
Opiskelijat pudottivat tennispallon 25 metriä korkean hyppyrin lähtotasanteelta. Ajat mitattiin matkapuhelimen ajanottolaitteella.
a)Ilmoita putoamisaika virherajoineen. Käytä virheen keskipoikkeamaa.
b) Laske ajan suhteellinen virhe.
c) Mitä virhelähteitä mittaukseen liittyy? Miten mittauksen voisi tehdä tarkemmaksi?
- Mittajien määrä, mittaukset ja pokkeamat.
Mitä enemmän mittajia on, sitä enemmän mittauksia saadaan, ja sitä tarkemmin mittauksesta tulee.