Palautettavat tehtävät 2020
Verkkotentti ti 28.4. klo 12:00 – 19:00
Linkki tenttiin
Tenttisivu ohjeistaa vaiheittaisin toimintaohjein. Opiskelijanumero on tärkeää kirjoittaa oikein, sillä järjestelmä päästää vain teidät kurssilaiset sisälle. Saatte tosin valita käyttämänne sähköpostiosoitteen itse.
Tenttiin on siis aikaa kolme tuntia, ja järjestelmä ajastaa aikahaarukan jokaiselle teistä valmiiksi. Tentti on mahdollista aloittaa aikaisintaan n. klo 12:00 ja myöhäisintään klo 19:00.
Kun sivusto on saanut vaatimansa tiedot Aloita-painikkeen painalluksella, saatte neljä tenttikysymystä suoraan sähköpostiinne. Tehtävänänne on luoda yksi pdf-tiedosto, jossa vastaatte saamiinne neljään kysymykseen perusopetuksen opetussuunnitelmaan sekä muihin oheisdokumentteihin (perusopetuslaki, tuntijako) tukeutuen. Toivon, että liitätte nimenne selkeästi sekä dokumentin nimeen että sen sisältöön.
Koska teknisiä ongelmia saattaa ilmetä itse kullekin, voit saada teknistä tukea lähettämällä minulle viestin joko tekstiviestinä tai Whatsappilla (kts. numero sähköpostissa). Ilmoita viestissäsi joko nimesi, opiskelijanumerosi tai molemmat, jotta pääsen tutkimaan asiaa mahdollisimman pikaisesti.
Tenttiin on siis aikaa kolme tuntia, ja järjestelmä ajastaa aikahaarukan jokaiselle teistä valmiiksi. Tentti on mahdollista aloittaa aikaisintaan n. klo 12:00 ja myöhäisintään klo 19:00.
Kun sivusto on saanut vaatimansa tiedot Aloita-painikkeen painalluksella, saatte neljä tenttikysymystä suoraan sähköpostiinne. Tehtävänänne on luoda yksi pdf-tiedosto, jossa vastaatte saamiinne neljään kysymykseen perusopetuksen opetussuunnitelmaan sekä muihin oheisdokumentteihin (perusopetuslaki, tuntijako) tukeutuen. Toivon, että liitätte nimenne selkeästi sekä dokumentin nimeen että sen sisältöön.
Koska teknisiä ongelmia saattaa ilmetä itse kullekin, voit saada teknistä tukea lähettämällä minulle viestin joko tekstiviestinä tai Whatsappilla (kts. numero sähköpostissa). Ilmoita viestissäsi joko nimesi, opiskelijanumerosi tai molemmat, jotta pääsen tutkimaan asiaa mahdollisimman pikaisesti.
Verkkotentti ti 28.4. klo 12:00 – 19:00 (kopio)
Linkki tenttiin
Tenttisivu ohjeistaa vaiheittaisin toimintaohjein. Opiskelijanumero on tärkeää kirjoittaa oikein, sillä järjestelmä päästää vain teidät kurssilaiset sisälle. Saatte tosin valita käyttämänne sähköpostiosoitteen itse.
Tenttiin on siis aikaa kolme tuntia, ja järjestelmä ajastaa aikahaarukan jokaiselle teistä valmiiksi. Tentti on mahdollista aloittaa aikaisintaan n. klo 12:00 ja myöhäisintään klo 19:00.
Kun sivusto on saanut vaatimansa tiedot Aloita-painikkeen painalluksella, saatte neljä tenttikysymystä suoraan sähköpostiinne. Tehtävänänne on luoda yksi pdf-tiedosto, jossa vastaatte saamiinne neljään kysymykseen perusopetuksen opetussuunnitelmaan sekä muihin oheisdokumentteihin (perusopetuslaki, tuntijako) tukeutuen. Toivon, että liitätte nimenne selkeästi sekä dokumentin nimeen että sen sisältöön.
Koska teknisiä ongelmia saattaa ilmetä itse kullekin, voit saada teknistä tukea lähettämällä minulle viestin joko tekstiviestinä tai Whatsappilla (kts. numero sähköpostissa). Ilmoita viestissäsi joko nimesi, opiskelijanumerosi tai molemmat, jotta pääsen tutkimaan asiaa mahdollisimman pikaisesti.
Tenttiin on siis aikaa kolme tuntia, ja järjestelmä ajastaa aikahaarukan jokaiselle teistä valmiiksi. Tentti on mahdollista aloittaa aikaisintaan n. klo 12:00 ja myöhäisintään klo 19:00.
Kun sivusto on saanut vaatimansa tiedot Aloita-painikkeen painalluksella, saatte neljä tenttikysymystä suoraan sähköpostiinne. Tehtävänänne on luoda yksi pdf-tiedosto, jossa vastaatte saamiinne neljään kysymykseen perusopetuksen opetussuunnitelmaan sekä muihin oheisdokumentteihin (perusopetuslaki, tuntijako) tukeutuen. Toivon, että liitätte nimenne selkeästi sekä dokumentin nimeen että sen sisältöön.
Koska teknisiä ongelmia saattaa ilmetä itse kullekin, voit saada teknistä tukea lähettämällä minulle viestin joko tekstiviestinä tai Whatsappilla (kts. numero sähköpostissa). Ilmoita viestissäsi joko nimesi, opiskelijanumerosi tai molemmat, jotta pääsen tutkimaan asiaa mahdollisimman pikaisesti.
to 16.4.
Loppu häämöttää niin peruskoulun sisältöjen kuin kurssin suhteen. Toiseksi viimeisenä palautettavana tehtävänä otamme edellisen tehtävän käänteisversion: tavoitteenasi on analysoida, miten oppilaiden vastauksissaan osoittama osaaminen voi vertautua avaruusgeometrian luonnoskriteeristöön.
Tehtävä. Etsi kotoasi joko WC-rullan tai talouspaperirullan hylsy. Tehtävänäsi on rakentaa hylsyn kanssa samanpohjainen ja yhtä korkea kartio ja perustella tämän mitat oikeiksi välivaiheittain laskemalla.
Tehtävä. Etsi kotoasi joko WC-rullan tai talouspaperirullan hylsy. Tehtävänäsi on rakentaa hylsyn kanssa samanpohjainen ja yhtä korkea kartio ja perustella tämän mitat oikeiksi välivaiheittain laskemalla.
| opetuksen tavoite | arvioinnin kohde | oppilaan oppimisen tavoite | arvosana 5 | arvosana 7 | arvosana 8 | arvosana 9 |
| T18 kannustaa oppilasta kehittämään taitoaan laskea pinta-aloja ja tilavuuksia | pinta-alojen ja tilavuuksien laskutaito | Oppilas tietää avaruuskappaleisiin liittyviä nimityksiä ja ominaisuuksia. Hän osaa laskea tasokuvioiden pinta-aloja sekä kappaleiden tilavuuksia ja vaipan pinta-aloja. Hän soveltaa tietojaan käytännön tilanteisiin, sekä tekee pinta-alayksiköiden, tilavuusyksiköiden ja vetomittojen välillä muunnoksia. | Oppilas muuntaa yleisimmin käytettyjä pinta-alan ja tilavuuden yksiköitä. Oppilas osaa laskea suorakulmion pinta-alan ja suorakulmaisen särmiön tilavuuden. | Oppilas muuntaa pinta-alan ja tilavuuden yksiöitä. Oppilas laskee yleisimpien tasokuvioiden pinta-alat ja kappaleiden tilavuudet. | Oppilas osaa pinta-ala- ja tilavuusyksiköiden muunnoksia. Oppilas laskee yksittäisen tasokuvion pinta-alan ja kappaleen tilavuuden sekä vaipan pinta-alan. Oppilas laskee keskuskulmaa vastaavan sektorin pinta-alan. | Oppilas laskee moniosaisen tasokuvion pinta.alan, kappaleen tilavuuden ja vaipan pinta-alan sekä hyödyntää osaamistaan ongelmanratkaisussa. |
ti 7.4.
Tämän kerran luennolla keskityttiin 8. luokan geometrian ja prosenttilaskennan kipukohtiin. Koska opettajan kuin opettajan arkeen kuuluu tehtävien nyhtäminen tyhjästä, pääset suunnittelemaan kolme prosenttilaskennan tehtävää. Käytä peruskoulun päättöarvioinnin kriteeristön luonnosversion tekstejä:
| opetuksen tavoite | arvioinnin kohde | oppilaan oppimisen tavoite | arvosana 5 | arvosana 7 | arvosana 8 | arvosana 9 |
| T13 tukea oppilasta laajentamaan ymmärrystään prosenttilaskennasta | prosentin käsite ja prosenttilaskenta | Oppilas ymmärtää prosentin ja prosenttiyksikön käsitteet ja kertoo niiden käytöstä eri tilanteissa. Hän laskee prosenttiosuuden, prosenttiluvun osoittaman määrän, sekä muutos- ja vertailuprosentin | Oppilas selittää, päättelee tai laskee prosenttiosuuden ja prosenttiluvun osoittaman määrän. | Oppilas laskee prosenttiosuuden, prosenttiluvun osoittaman määrän kokonaisuudesta sekä laskee muutoksen suuruuden ja muutoksen prosentteina. | Oppilas laskee prosenttiosuuden, prosenttiluvun osoittaman määrän kokonaisuudesta sekä muutos- ja vertailuprosentin eri tilanteissa. | Oppilas ymmärtää prosentin ja prosenttiyksikön välisen eron, Oppilas tekee suhteellista vertailua ja käyttää prosenttilaskentaa eri tilanteissa. |
- tehtävä 1: symbolis-symbolinen (numeraalinen tehtävänanto, numeraalinen vastaus)
- täysin oikea ratkaisu osoittaa arvosanan 5 saavuttamiseen vaaditun osaamisen
- tehtävä 2: kuvallis-symbolinen (kuvallinen tehtävänanto, numeraalinen vastaus)
- täysin oikea ratkaisu osoittaa arvosanan 7 saavuttamiseen vaaditun osaamisen
- tehtävä 3: verbaalis-verbaalinen (sanallinen tehtävänanto, sanallinen vastaus)
- täysin oikea ratkaisu osoittaa arvosanan 9 saavuttamiseen vaaditun osaamisen
to 2.4.
Varsin algebrantäyteisen luennon jälkimainingeissa pääsette larppaamaan oppilaita.
- Keksi mahdollisimman monta erilaista väärää tapaa ratkaista seuraavat yhtälöt. Yritä sanallistaa jokainen keksimäsi virhekäsitys. Yritä siis perustella väärä vastauksesi oikeaksi – oppilastyyliin.
- 2x = 6
- 3(x – 8) = 28
- x² = 16
- Toimi samoin kuin edellisessä tehtävässä: yritä siis keksiä mahdollisimman monta väärää vastausta ajatusketjuineen, tällä kertaa sanallisiin tehtäviin.
- "Maila ja pallo maksavat yhteensä 1,10 €, ja maila maksaa 1,00 € enemmän kuin pallo. Kuinka monta euroa pallo siis maksaa?"
- "Jos viideltä laitteelta kestää viisi minuuttia valmistaa viisi tuotetta, kuinka kauan sadalta samanlaiselta laitteelta kuluu sadan tuotteen valmistamiseen?"
- "Järven lumpeet kasvavat joka päivä niin, että ne peittävät seuraavana päivänä kaksi kertaa niin suuren alan kuin edellisenä. Jos järvi peittyy 48 päivässä, kuinka monessa päivässä järvi oli peittynyt puoliksi?"
ti 31.3.
Tämänpäiväisen jaollisuus- ja kirjainlaskentaluennon siivittämänä pääsette tutkimaan tehtävien laadinnassa hyödyllisiä jaollisuuslauseita. Osoita siis seuraavat todeksi m.o.t.-tyylillä joko suoralla, epäsuoralla tai induktiivisella todistuksella tai vastaesimerkillä.
Lause. Olkoot n ja m kokonaislukuja. Jos on olemassa sellainen k, että k | n ja k | m, niin k | (n+m).
Lause. Olkoot n ja m kokonaislukuja. Jos on olemassa sellainen k, että k | n ja k | m, niin k | (n+m).
Lause. Olkoon n kokonaisluku. Tällöin on olemassa sellainen k ≤ √n, jolle k | n.
Lause. Osoita, että on olemassa sellaiset kokonaisluvut n, m ja k, että k | nm tekijä mutta k ei ole luvun n tekijä ja k ei ole luvun m tekijä.
to 26.4.
Torstain luennolla in a nutshell keskusteltiin jo jonkin verran, aiheena reaaliluvut lukusuoralla sekä geometria seiskaluokalla. Kuten luennon loppupuolella mainitsinkin, tämän kerran palautettava tehtävä liittyy tehtävänantoihin ja haastavuustasoon.
Totuttuun tapaan luomuksena syntyy tiedosto, jonka nimeämislogiikka on "Janne Valtonen 26 maaliskuuta.pdf", ja tämän sisältönä pääset luomaan alaspäin eriyttävän tehtävän, perustehtävän, haastavan tehtävän sekä bonustehtävän, jonka aiheena on pisteet, suorat sekä janat ja jonka ideana on selvittää mahdollisuuksien lukumääriä.
Ota huomioon tehtäviä laatiessasi viime pohdinnasta tutut viitekehykset (Oppimisen viitekehyksiä) sekä taustainspiraationa toimivat euklidisen geometrian aksioomat (Euklidisen geometrian aksioomat). Perustele myös, miksi tehtäväsi osuvat juuri kullekin haastavuustasolle.
Totuttuun tapaan luomuksena syntyy tiedosto, jonka nimeämislogiikka on "Janne Valtonen 26 maaliskuuta.pdf", ja tämän sisältönä pääset luomaan alaspäin eriyttävän tehtävän, perustehtävän, haastavan tehtävän sekä bonustehtävän, jonka aiheena on pisteet, suorat sekä janat ja jonka ideana on selvittää mahdollisuuksien lukumääriä.
Ota huomioon tehtäviä laatiessasi viime pohdinnasta tutut viitekehykset (Oppimisen viitekehyksiä) sekä taustainspiraationa toimivat euklidisen geometrian aksioomat (Euklidisen geometrian aksioomat). Perustele myös, miksi tehtäväsi osuvat juuri kullekin haastavuustasolle.
ti 24.3.
Palautettava tehtävä pureutuu tällä kertaa tehtävänantojen epätäsmällisyyksiin ja sudenkuoppiin.
Esittelin luennon loppupuolella reaalilukujen laskutoimituksia eriyttävän tehtäväsarjan idean:
"Ratkaise seuraavat tehtävät vihkoosi.
1. a) Mikä lämpötila on viisi astetta lämpimämpi kuin 1 °C?
1. b) 1 + 5 =
2. a) Mikä lämpötila on kolme astetta lämpimämpi kuin –1 °C?
2. b) –1 + 3 =
3. a) Mikä lämpötila on seitsemän astetta kylmempi kuin 4 °C?
3. b) –7 + 4 =
4. a) Mikä lämpötila on yhden asteen kylmempi kuin –2 °C?
4. b) –2 – 1 =
Muista tarkistaa vastauksesi kirjan takaa."
Pohdi seuraavia seikkoja vapaamuotoisessa, logiikalla "Janne Valtonen 24 maaliskuuta.pdf" nimetyssä dokumentissa. Muista lähettää dokumenttisi vastauksena tähän viestiin.
- Mitä tehtävien laadinnan viitekehyksiä (https://peda.net/id/1d2328e4b53) ylläolevat tehtävät 1 – 4 hyödyntävät
- Ovatko tehtävät mielestäsi ylöspäin vai alaspäin eriyttäviä? Miksi?
- Millä eri tavoilla oppilas voi epäonnistua tehtävien ratkaisemisessa?
- Keksi tehtäväpaketin jatkoksi samanhenkinen mutta avoin tehtävä 5.
to 19.3.
Tämänkertainen luento pureutui entistä syvemmälle perusopetuksen nivelvaiheisiin.
Edellisellä kerralla käsitellyn opettaja- ja kouluyhteistyön lisäksi esititte kysymyksiä matematiikan ydinsisältöihin liittyen: siihen, mitä luokanopettaja voi tehdä oppilaidensa matemaattisen tason takaamiseksi, ja siihen, miten aineenopettaja kykenee tunnistamaan tuen tarpeen nivellyksen seurauksena saaduista etukäteistiedoista, pedagogisista asiakirjoista sekä alkutesteistä ja seuloista.
Osa kysymyksistä jäi ratkaisujoukoiltaan puoliavoimiksi väleiksi [a,b), jossa a = tänään ja b = ensi tiistaina. Tämän varsin aiheeseen liittyvän vitsikkään sutjautuksen siivittämänä palautettava tehtävä ensi kerralle liittyy yläkoulun matematiikan sisältöjen metatasoon eli siihen, miten yliopistomatematiikka liittyy aineenopettajan työhön yläkoulun pyörteissä.
Alamme kerta kerralta taklata yläkoulun aihealueita. Ensi kerralla luvassa reaaliluvut ja rationaaliluvut, yläkoulukielelle dubatussa muodossa "murtoluvut" ja "kaikki luvut, joita oppilas voi keksiä".
- Määrittele reaaliluvut. Anna esimerkki luvusta, joka ei ole reaaliluku – perustelua unohtamatta.
- Määrittele ekvivalenssirelaatio. Anna vapaavalintainen esimerkki peruslaskutoimituksiin liittyvästä, funktioihin liittyvästä sekä joukkoihin liittyvästä ekvivalenssirelaatiosta, siis kolme yhteensä.
- Määrittele rengas. Anna esimerkki renkaasta, jossa tulon nollasääntö toimii, ja renkaasta, jossa se ei toimi.
Edellisellä kerralla käsitellyn opettaja- ja kouluyhteistyön lisäksi esititte kysymyksiä matematiikan ydinsisältöihin liittyen: siihen, mitä luokanopettaja voi tehdä oppilaidensa matemaattisen tason takaamiseksi, ja siihen, miten aineenopettaja kykenee tunnistamaan tuen tarpeen nivellyksen seurauksena saaduista etukäteistiedoista, pedagogisista asiakirjoista sekä alkutesteistä ja seuloista.
Osa kysymyksistä jäi ratkaisujoukoiltaan puoliavoimiksi väleiksi [a,b), jossa a = tänään ja b = ensi tiistaina. Tämän varsin aiheeseen liittyvän vitsikkään sutjautuksen siivittämänä palautettava tehtävä ensi kerralle liittyy yläkoulun matematiikan sisältöjen metatasoon eli siihen, miten yliopistomatematiikka liittyy aineenopettajan työhön yläkoulun pyörteissä.
Alamme kerta kerralta taklata yläkoulun aihealueita. Ensi kerralla luvassa reaaliluvut ja rationaaliluvut, yläkoulukielelle dubatussa muodossa "murtoluvut" ja "kaikki luvut, joita oppilas voi keksiä".
- Määrittele reaaliluvut. Anna esimerkki luvusta, joka ei ole reaaliluku – perustelua unohtamatta.
- Määrittele ekvivalenssirelaatio. Anna vapaavalintainen esimerkki peruslaskutoimituksiin liittyvästä, funktioihin liittyvästä sekä joukkoihin liittyvästä ekvivalenssirelaatiosta, siis kolme yhteensä.
- Määrittele rengas. Anna esimerkki renkaasta, jossa tulon nollasääntö toimii, ja renkaasta, jossa se ei toimi.
ti 17.3.
Tämän päivän illan verkkoluennoilla totuteltiin striimausluentoihin, keskusteltiin valmiuslain tuomasta poikkeusajasta sekä matematiikan opettamisen sisältönä ala- ja yläkoulun välisestä jatkumosta ja tämän nivelvaiheen haasteista. Lisäksi keskustelimme tentin detaljeista (tai ainakin luennoitsija luennoi näistä itselleen).
Laadi luennon jälkitehtävänä noin sivun mittainen erittely ja pohdinta seuraavista seikoista:
Laadi luennon jälkitehtävänä noin sivun mittainen erittely ja pohdinta seuraavista seikoista:
- Mitä tarkoittaa peruskoulussa nivelvaihe? Entä niveltäminen?
- Miksi oppilaita nivelletään? Mitä hyötyä niveltämisestä on?
- Minkä tietojen ja dokumenttien siirtyminen koulusta toiseen on kriittistä nivellysprosessissa?
- Miten nivellysyhteistyö koulujen välillä suhteutuu opettajien työaikaan?
- Mitä matematiikan aineenopettaja voi tehdä 7. luokan alussa, jotta syöttökoulujen erot, olivatpa ne suuret tai pienet, tasoittuisivat?
Luo vastauksistasi pdf-tiedosto, nimeä se logiikalla "Janne Valtonen 17 maaliskuuta.pdf" ja lähetä se vastauksesi liitteenä saamaasi massasähköpostiviestiin, tai muutoin luennoitsijan tiedostonhallinta ei enää ole triviaalia.
to 12.3.
Toisella (ja poikkeustilan vuoksi myös viimeisellä) lähiopetuskerralla ratkoimme varsin haastavia tehtäviä.
Jos olit kyseiseltä kerralta poissa, laadi pdf-muotoinen dokumentti, ja nimeä se logiikalla:
"Janne Valtonen 12 maaliskuuta.pdf"
Dokumentin tulee sisältää ratkaisusi (tai ratkaisuyrityksesi) seuraaviin neljään pulmatehtävään.
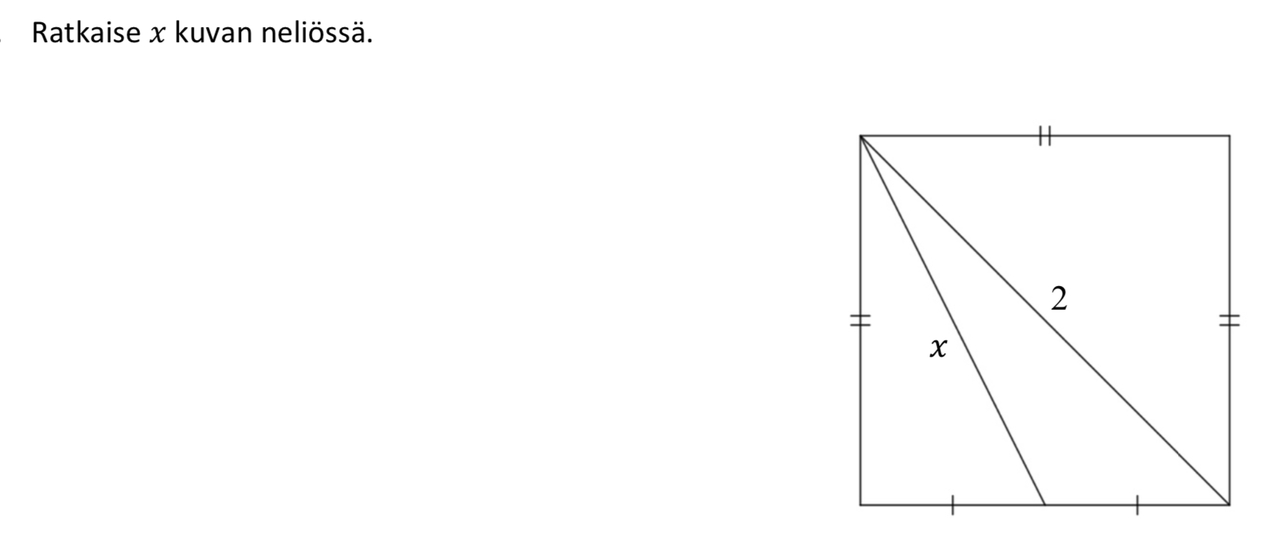
ti 10.3.20 Perusopetusta ohjaavat asiakirjat
Ensimmäisellä lähiopetuskerralla utelin teidän pohjatietojanne sekä alkukäsityksiänne siitä, minkälaista peruskoulun matematiikka on.
Jos olit kyseiseltä kerralta poissa, laadi pdf-muotoinen noin kahden sivun dokumentti, ja nimeä se logiikalla:
"Janne Valtonen 10 maaliskuuta.pdf"
Dokumentin tulee sisältää alkutiedot:
- pääaineesi
- suorittamasi matematiikan opintopisteet
- lista kolmesta sinulle kolmesta tutuimmasta matematiikan kurssista
Alkutietojen lisäksi haluan kuulla sinulta pohdintaa opettajan työstä. Voit lähestyä esimerkiksi seuraavien apukysymysten näkökulmista:
- Mitkä ovat opettajan tärkeimmät työkalut?
- Mitkä tekijät ohjaavat opettajan työtä?
- Mitkä toimijat ohjaavat opettajan työtä?
- Mitkä dokumentit ohjaavat opettajan työtä?
Jos olit kyseiseltä kerralta poissa, laadi pdf-muotoinen noin kahden sivun dokumentti, ja nimeä se logiikalla:
"Janne Valtonen 10 maaliskuuta.pdf"
Dokumentin tulee sisältää alkutiedot:
- pääaineesi
- suorittamasi matematiikan opintopisteet
- lista kolmesta sinulle kolmesta tutuimmasta matematiikan kurssista
Alkutietojen lisäksi haluan kuulla sinulta pohdintaa opettajan työstä. Voit lähestyä esimerkiksi seuraavien apukysymysten näkökulmista:
- Mitkä ovat opettajan tärkeimmät työkalut?
- Mitkä tekijät ohjaavat opettajan työtä?
- Mitkä toimijat ohjaavat opettajan työtä?
- Mitkä dokumentit ohjaavat opettajan työtä?
Sinulla ei ole tarvittavia oikeuksia lähettää mitään.


