[[$P(x)=ax^2+bx+c, \text{ missä }a\neq0, b \text{ ja } c \in \mathbb{R}$]]


Kuvaaja
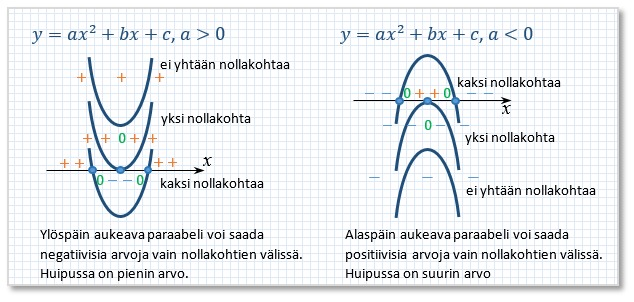
Toisen asteen polynomifunktion kuvaaja on
paraabeli. Jos toisen asteen termin kerroin on positiivinen, puhutaan
ylöspäin aukeavasta paraabelista ja jos kerroin on negatiivinen, puhutaan
alaspäin aukeavasta paraabelista.
Nollakohdat
Toisen asteen polynomilla on joko yksi, kaksi tai ei yhtään nollakohtaa. Nollakohdat, eli
juuret saadaan ratkaistua ratkaisemalla yhtälö [[$P(x)=0$]].
Funktion merkki
Toisen asteen polynomifunktion etumerkki voi vaihtua vain nollakohdassa aivan kuin ensimmäisen asteen polynomifunktionkin. Ratkaistaessa toisen asteen epäyhtälöitä tutkitaankin funktion merkin vaihtumista nollakohdassa ja merkkiä nollakohtien molemmin puolin.