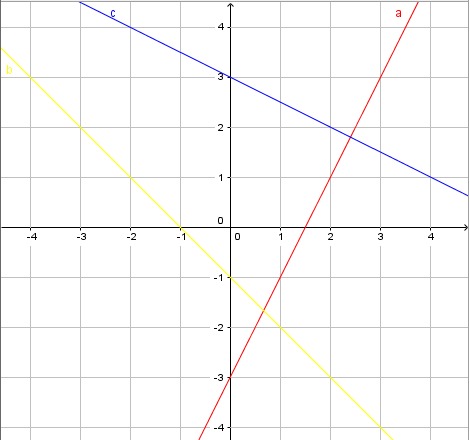
Suoran yhtälö
Ohje
- Klikkaa Geogebra-ohjelma auki linkistä omaan ikkunaan (eli klikkaa hiiren oikealla painikkeella linkkiä ja valitse "Avaa uudessa ikkunassa").
- Klikkaa avautuvan koordinaatiston pohjaa hiiren oikealla painikkeella ja valitse Koordinaatistoruudusto.
- Klikkaa oikeasta yläkulmasta "kolmea raitaa", sieltä Näkymät ja sitten Algebra
NYT TYÖSKENTELYPOHJASI ON VALMIS!