4.4 Hajoamislaki
Johdantovideo
Miksi näytteen mitattu aktiivisuus vähenee? Millainen matemaattinen malli kuvaa aktiivisen aineen määrää suhteessa kuluneeseen aikaan?
Radioaktiivisuuden taustaa
Alkuaineilla on eri isotooppeja, joista alle 10 % on vakaita. Epävakaat isotoopit hajoavat jollain aiemmin esitellyistä tavoista. Yleensä jokainen isotooppi hajoaa vain tietyllä tavalla, mutta esimerkiksi hyvin raskaat isotoopit voivat joskus hajota sekä alfahajoamisen, että spontaanin fission kautta. Alla olevaan graafiin on sijoitettu kaikki tunnetut isotoopit. Vaaka-askelilla on isotoopin järjestysluku Z, eli protonien lukumäärä ja pystyakselilla isotoopin neutronien lukumäärä. Eri värit kuvaavat isotooppien pysyvyyttä.
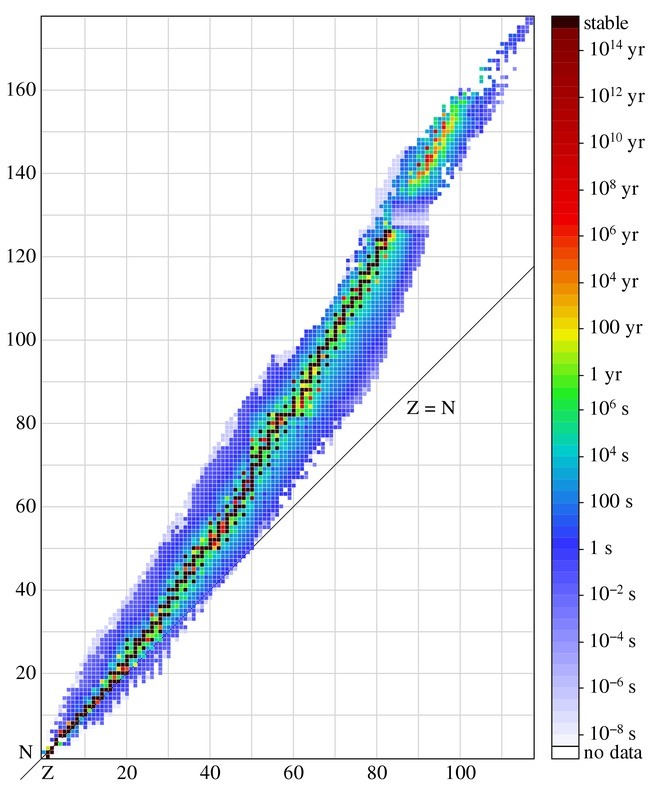
Graafissa pysyvät isotoopit on merkitty mustalla. Kevyimmissä on protoneita ja neutroneita likimäärin yhtä paljon, eli suhde N/Z on lähellä yhtä. Raskaammissa pysyvissä ytimissä suhde N/Z on suurempi. Vahvan vuorovaikutuksen on helpompi liittää yhteen neutroneja kuin protoneja, koska neutronien välillä ei esiinny sähköistä poistovoimaa. Radioaktiivinen hajoaminen tapahtuukin niin, että tytärytimen N/Z-suhde on lähempänä optimaalista kuin emoytimen.
Satunnaisuus on luonteenomaista radioaktiiviselle hajoamiselle. Tämä perustuu nukleonien aalto-hiukkasdualistisiin ominaisuuksiin. Luvussa 2 tutustuttiin kvanttimekaniikan periaatteisiin, joiden mukaan hiukkasilla ei ole tarkkaa paikkaa. Sen sijaan hiukkasten sijainnilla on todennäköisyysjakauma. Ytimen nukleonit ovat vahvan vuorovaikutuksen vaikutuksen alaisena, eikä niiden liike-energia riitä ytimestä karkaamiseen. Nukleonien sijainnin todennäköisyysjakauma voi ulottua kuitenkin ytimen ulkopuolelle, mikä mahdollistaa tunneloitumisen. Tunneloitumisen myötä hiukkanen pääsee ytimen ulkopuolelle, vaikka klassisen fysiikan mukaan se ei voisi sinne liikkua. Hyvin raskaiden ydinten tapauksessa hiukkaset erkanevat ytimistä heliumytimien muodostamina kokonaisuuksina, eli alfahiukkasina. Paettuaan vahvan vuorovaikutuksen voimakkaimman vaikutuksen alueelta alfahiukkasen ja ytimen välinen sähköinen hylkimisvoima sinkoaa ne suurella vauhdilla poispäin toisistaan.
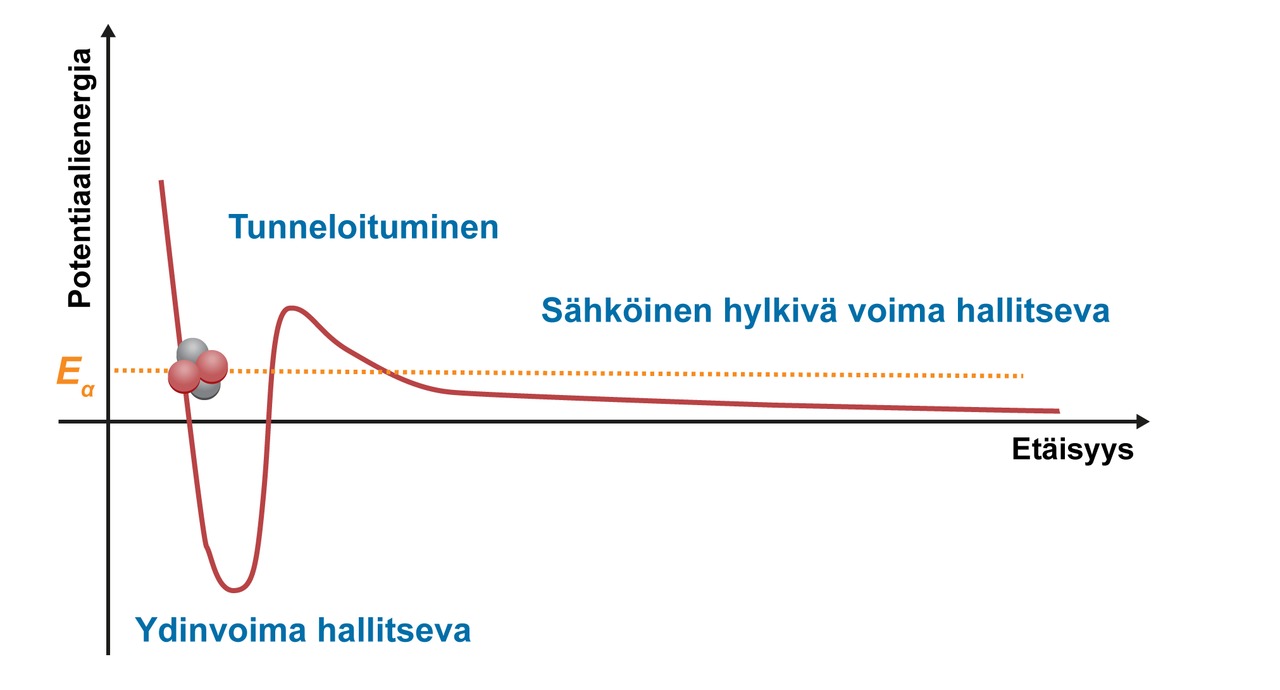Alfahiukkasen energia ytimen läheisyydessä.Aktiivisuus
Kvanttifysiikan mukaan radioaktiivisuus on aidosti satunnainen ilmiö. Vastaavaan satunnaisuuteen on tutustuttu käsiteltäessä elektronin sijaintia tai atomin viritystilan purkautumista. Yksittäisen radioaktiivisen ytimen hajoamishetkeä ei voida edes teoriassa ennustaa. Mitä sen sijaan voidaan ennustaa, on ytimen hajoamisen todennäköisyys. Tätä kuvataan suureella hajoamisvakio, [[$ \lambda $]].
Hajoamisvakio ilmaisee isotoopin yhden ytimen todennäköisyyden hajota sekunnin aikana. Mitä suurempi se on, sitä epävakaampi isotooppi on kyseessä. Hajoamisvakion suuruus on tyypillisesti luku väliltä 0...1 ja yksikkö 1/s. Esimerkiksi fluori-20:n hajoamisvakio on 0,063 1/s. Mikäli näytteessä on 1000 aktiivista fluoriydintä, hajoaa niitä sekunnin aikana n. 63 kappaletta (0,063[[$ \cdot $]]1000). Hajoamisten määrä aikayksikköä kohden voidaan yleisesti laskea hajoamisvakion [[$ \lambda $]] ja hiukkasten lukumäärän N tulona: [[$ \lambda N $]]. Tämä tulo on aktiivisuus (A):
[[$ \quad A= \lambda N $]].
Aktiivisuus (A) ilmaisee näytteessä tapahtuvien hajoamisten määrän aikayksikköä kohden. Sen yksikkö on becquerel (Bq), jolle pätee 1 Bq = 1/s. Yksikkö on nimetty ranskalaisen fyysikon Henri Becquerelin (1852-1908) mukaan.
Ytimen hajotessa syntyy säteilyä, joka voidaan havaita säteilyilmaisimella. Mikään säteilymittari ei kuitenkaan havaitse kaikkia näytteessä tapahtuvia hajoamisia, sillä säteily leviää joka suuntaan ja absorboituu ympäristöiviin aineisiin. Säteilymittari mittaakin suhteellista aktiivisuutta, joka on tietty prosentuaalinen osuus näytteen koko aktiivisuudesta.
Aktiivisuus
Aktiivisuus A ilmaisee aineessa tapahtuvien hajoamisten lukumäärän aikayksikköä kohden.
[[$ \quad A =\lambda N $]]
N on ydinten lukumäärä ja [[$ \lambda $]] isotoopin hajoamisvakio.
Radioaktiivisen näytteen ydinten lukumäärää on käytännössä mahdotonta laskea. Makroskooppisella tasolla voidaan sen sijaan mitata näytteen massa. Massa m on suoraan verrannollinen ydinten lukumäärään N, mitä ilmaisee yhtälö
[[$ \quad N=\dfrac{m}{m_{\text{atomi}}} $]]
Eri isotooppien atomimassat esitetään fysiikan taulukoissa. Ne annetaan atomimassayksikön (u) avulla. Atomimassayksikkö on kilogrammoina 1,66053886 · 10-27 kg. Näiden tietojen avulla on laskettavissa tietyn massaisen tunnettua isotooppia olevan näytteen ydinten lukumäärä. Esimerkiksi 10 mg näyte radioaktiivista jodi-131 -isotooppia sisältää seuraavan määrän ytimiä:
[[$ \quad N=\dfrac{m}{m_{\text{atomi}}}=\dfrac{10\cdot 10^{-6}\text{ kg}} {130,906124\cdot 1,66053886\cdot 10^{-27} {\text{ kg}}}\approx 4,0 \cdot 10^{19} $]]
Hajoamislaki
Radioaktiivinen ydin muuttuu hajotessaan toiseksi ytimeksi. Aktiivisten ydinten määrä siis vähenee ajan kuluessa. Näytteen aktiivisuus on määritelmänsä [[$ A=\lambda N $]] mukaan suoraan verrannollinen aktiivisten ydinten lukumäärään. Siksi myös aktiivisuus vähenee, mikä havaittiin johdantovideolla. Tarkastellaan, millaisella matemaattisella mallilla voidaan esittää ydinten lukumäärän riippuvuutta ajasta.
Yhden becquerelin aktiivisuus tarkoittaa, että aktiivisten ydinten määrä vähenee yhdellä sekunnissa. Aktiivisuus ilmaisee yleisemmin ydinten määrän muutosnopeuden. Määrän väheneminen tarkoittaa negatiivista muutosta, eli
[[$ \quad -A=\dfrac{\Delta N}{\Delta t} $]]
Ydinten määrä ajan funktiona merkitään [[$ N(t) $]]. Aktiivisuus on tällöin [[$ \lambda N(t) $]], ja muutosnopeus on ydinten lukumäärän derivaatta. Edellinen yhtälö voidaan siis muotoilla seuraavasti:
[[$ \quad N'(t)=-\lambda N(t)$]]
Yhtälö, jossa esiintyy funktio ja sen derivaatta, on niin sanottu differentiaaliyhtälö. Differentiaaliyhtälöitä ei käsitellä lukiomatematiikassa, mutta ratkaisu voidaan päätellä. Yhtälön toteuttavat funktiot, jotka ovat muotoa [[$ N(t) = ke^{-\lambda t} $]], jossa k on vakio. Tämä voidaan todeta yhdistetyn funktion ja eksponenttifunktion derivointisääntöjen perusteella:
[[$ \quad D N(t) =D ke^{-\lambda t}=-k\lambda e^{-\lambda t}=-\lambda N(t) $]]
Funktion vakiotermin k merkitys voidaan päätellä laskemalla funktion arvo ajanhetkellä 0 s:
[[$ \quad N(0 \text{ s})=ke^{-\lambda \cdot 0 \text{ s}}=k \cdot 1 =k $]]
Vakiotermi ilmaisee ydinten lukumäärän tarkastelun alkuhetkellä, mitä merkitään [[$ N_0 $]]. Näin on perusteltu radioaktiivisten ydinten lukumäärää ajanhetkellä t ilmaiseva hajoamislaki:
[[$ \quad N(t) =N_0 e^{-\lambda t} $]]
Myös näytteen aktiivisuus vähenee eksponentiaalisesti ajan suhteen. Tämä on selvää, sillä jokaisella ajanhetkellä aktiivisuus on hajoamisvakion ja ydinten lukumäärän tulo. Siis
[[$ \quad A(t) =A_0 e^{-\lambda t} $]]
Hajoamislaki
Radioaktiivisten ydinten lukumäärä N vähenee eksponentiaalisesti ajan t suhteen.
[[$ \quad N(t) =N_0 e^{-\lambda t} $]]
N0 on ydinten lukumäärä alussa ja [[$ \lambda $]] isotoopin hajoamisvakio.
Myös näytteen aktiivisuus A vähenee eksponentiaalisesti.
[[$ \quad A(t) =A_0 e^{-\lambda t} $]]
Puoliintumisaika
Havainnollinen radioaktiivisten isotooppien pysyvyyttä kuvaava suure on puoliintumisaika, T1/2. Se on aika, jonka kuluessa yksittäinen ydin hajoaa 50 %:n todennäköisyydellä. Jos ytimiä on paljon, kuten missä tahansa tavanomaisessa näytteessä, niiden määrä likimäärin puolittuu puoliintumisajan kuluessa. Samalla näytteen aktiivisuus laskee puoleen. Tämä on eksponentiaalisen mallin yleinen ominaisuus: tietyn ajan kuluessa prosentuaalinen muutos on aina yhtä suuri.
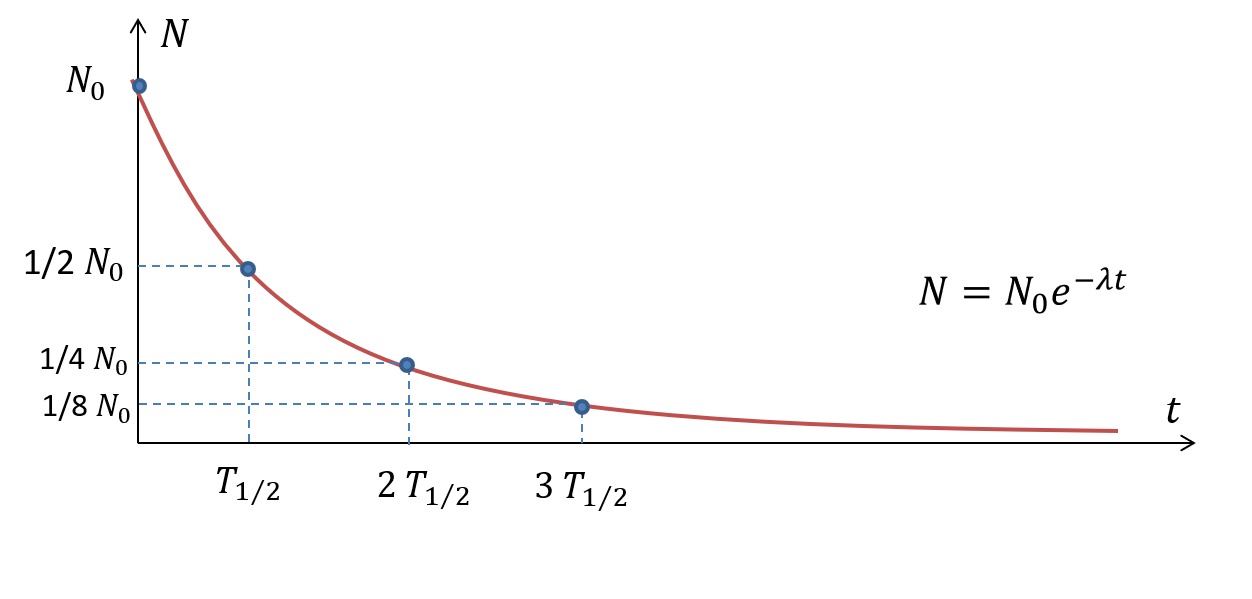Ydinten määrä puoliintuu aina tietyn ajan kuluessa.Puoliintumisajan yhteys isotoopin hajoamisvakioon voidaan ratkaista hajoamislain perusteella. Ratkaistaan hajoamislaista aika, jolloin ydinten määrä on puolet alkuperäisestä.
[[$ \quad \begin {align*} A_0 e^{-\lambda T_{1/2}}&=\frac {1}{2} A_0 &|& :A_0 \\ \, \\ e^{-\lambda T_{1/2}}&=\frac {1}{2} \lambda &|& \text{(otetaan logaritmi puolittain)} \\ \, \\ -\lambda T_{1/2} &= \ln \frac {1}{2} &|& \text{(sovelletaan logaritmin laskusääntöjä)} \\ \, \\ -\lambda T_{1/2} &= -\ln 2 \\ \, \\ T_{1/2} &= \frac {\ln 2}{\lambda} \\ \end {align*} $]]
Puoliintumisaika
Puoliintumisaika T1/2 on aika, jossa puolet radioaktiivisen aineen ytimistä hajoaa. Puoliintumisajan ja hajoamisvakion [[$ \lambda $]] välillä on riippuvuus
[[$ \quad T_{1/2} = \dfrac {\ln 2}{\lambda} $]]
Alla olevassa simulaatiossa voi havainnoida ydinten lukumäärän muutosta ajan suhteen.
Esimerkkejä
Esimerkki 1
Kuinka suuri on aktiivisuus 1,0 milligrammassa radium-223 -isotooppia? Kuinka suuri kokonaisenergia on vapautunut yhden radiumin puoliintumisajan kuluttua?
Esimerkki 2
Lääketieteellisen merkkiaineen aktiivisuus sen valmistuksen jälkeen on 45 MBq. Aktiivisuus on 34 MBq, kun aine tuodaan sairaalaan 16 tunnin kuluttua.
a) Määritä aineen puoliintumisaika.
b) Aine on käyttökelpoista, kunnes sen kokonaisaktiivisuus laskee alle 5,0 MBq. Kuinka kauan tähän kuluu aikaa?