Polynomin jaollisuus

Jos [[$x_1$]] on polynomin nollakohta, niin silloin [[$(x-x_1)$]] on polynomin tekijä. Kääntäen pätee myös, että jos polynomilla on tekijänä [[$(x-x_1)$]], niin silloin [[$x_1$]] on polynomin nollakohta.

Jos polynomilla ei ole reaalilukujen joukossa yhtään nollakohtaa, sitä ei voida jakaa reaalilukutekijöihin ja sanotaan, että polynomi on jaoton.

​

Polynomin jakolause
Jos [[$x_1$]] on polynomin nollakohta, niin [[$(x-x_1)$]] on polynomin tekijä.

​
Seuraus:
Mikä tahansa polynomi
[[$P(x)=a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0, $]] voidaan kirjoittaa tulomuotoon:
[[$P(x)=a_n (x-x_1)(x-x_2)\dots(x-x_n)$]]
missä [[$\{ x_1, x_2, ..., x_n \} $]]ovat yhtälön [[$P(x)=0$]] ratkaisut, eli [[$P$]]:n nollakohdat ja [[$a_n$]] on korkeimman asteisen termin kerroin.​

Esimerkki 1.
Määritä sellainen 3. asteen polynomi, jonka nollakohdat ovat:
[[$x=-2$]], [[$x=1$]] ja [[$x=3$]].
Ratkaisu:
Muodostetaan polynomin tulomuotoinen esitys nollakohtien avulla:
[[$P(x)=(x-(-2))(x-1)(x-3)$]]

Lasketaan sulut auki:
[[$\begin{align}&=(x+2)(x-1)(x-3)\\&=(x^2+x-2)(x-3)\\&=x^3-3x^2+x^2-3x-2x+6\\&=x^3-2x^2-5x+6\end{align}$]]
Vastaus:
Eräs 3. asteen polynomi, jonka nollakohdat ovat [[$x=-2$]], [[$x=1$]] ja [[$x=3$]] on [[$P(x)=x^3-2x^2-5x+6$]]


Esimerkki 2.
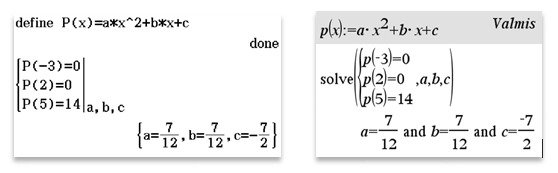
Määritä se toisen asteen polynomi,
jonka nollakohdat ovat [[$x_1=-3$]] ja [[$x_2=2$]]
ja [[$P(5)=14$]].

Ratkaisu:
Yleisen polynomien jakolauseen mukaan
[[$P(x)=a(x-x_1)(x-x_2),$]] missä [[$x_1$]] ja [[$x_2$]] ovat polynomin nollakohdat.

[[$\begin{align}P(x)&=a (x-(-3)) (x-2)\\&=a(x+3)(x-2)\\&=ax^2+ax-6a\end{align}$]]

Ratkaistaan [[$a$]] ehdosta [[$P(5)=14$]]

[[$\begin{align}P(5)&=14\\a(5+3)(5-2)&=14\\a&=\frac{14}{(5+3)(5-2)}\\a&=\frac{14}{24}=\frac{7}{12}\end{align}$]]

Kysytty polynomi on

[[$\begin{align}P(x)&=\frac{7}{12} (x+3) (x-2)\\&=\frac{7}{12}x^2+\frac{7}{12}x-\frac{7}{2}\end{align}$]]

Vinkki Voit selvittää 2. asteen polynomin kertoimet [[$a, b, c$]] myös määrittelemällä laskimeen yleisen toisen asteen polynomifunktion [[$P(x)=ax^2+bx+c$]] ja ratkaisemalla sen jälkeen kolmen yhtälön yhtälöryhmä annetuilla ehdoilla.