1.2. Polynomin jakaminen tekijöihin
Polynomin tulomuoto
Polynomin jakaminen tekijöihin tarkoittaa polynomin esittämistä kahden tai useamman polynomin tulona. Polynomia esittävä summalauseke esitetään siis tulomuodossa.
Esimerkiksi seuraavat polynomit tarkoittavat samaa:
Summalauseke: [[$5x^4+10x^3-185x^2+50x+840$]]
Tulomuoto: [[$5(x-3)(x+2)(x-4)(x+7)$]]
Tekijöihin jakamisesta on hyötyä sievennettäessä rationaalilausekkeita tai määritettäessä polynomin nollakohtia, eli polynomiyhtälön [[$P(x)=0$]] ratkaisuja.
Esimerkiksi seuraavat polynomit tarkoittavat samaa:
Summalauseke: [[$5x^4+10x^3-185x^2+50x+840$]]
Tulomuoto: [[$5(x-3)(x+2)(x-4)(x+7)$]]
Tekijöihin jakamisesta on hyötyä sievennettäessä rationaalilausekkeita tai määritettäessä polynomin nollakohtia, eli polynomiyhtälön [[$P(x)=0$]] ratkaisuja.
Yhteisen tekijän erottaminen
Yhteinen tekijä
Polynomi on mahdollista kirjoittaa tulomuotoon, jos termeille löytyy yhteinen tekijä. Yhteisen tekijän erottaminen on tulon osittelulain soveltamista taaksepäin.
| Esimerkki 1. |
|---|
| Jaa tekijöihin, eli esitä kahden tai useamman polynomin tulona [[$21x^2-28$]]. |
| Ratkaisu: [[$21x^2-28=7\cdot3x^2-7\cdot4=7(3x^2-4)$]] |
[[$21x^2-28=7(3x^2-4)$]] |
| Esimerkki 2. |
|---|
| Jaa tekijöihin, eli esitä kahden tai useamman polynomin tulona [[$6x^2+8x$]]. |
| Ratkaisu:
Jakamalla molemmat termit tekijöihin nähdään, että yhteinen tekijä on [[$2x$]]. Kertolaskun osittelulain perusteella polynomi voidaan kirjoittaa muotoon: [[$6x^2+8x = 3\cdot \underbrace{2\cdot x}_{2x} \cdot x+ 4\cdot \underbrace{2\cdot x}_{2x} = 2x(3x+4)$]] |
[[$6x^2+8x=2x(3x+4)$]] |
| Esimerkki 3. |
|---|
| Jaa tekijöihin, eli esitä kahden tai useamman polynomin tulona [[$(x+2)^4+(x+2)^3$]]. |
| Ratkaisu: Potensseja ei kannata laskea auki, kyseessä on samankantaiset potenssit. Erotetaan yhteinen tekijä [[$(x+2)^3$]]. [[$(x+2)^4+(x+2)^3 =\underbrace{\underline{(x+2)^3}\cdot(x+2)}_{(x+2)^4}+\underbrace{\underline{(x+2)^3}\cdot 1}_{(x+2)^3}$]] [[$ = (x+2)^3\left( (x+2) + 1\right) = (x+2)^3(x+3) $]] |
[[$(x+2)^4+(x+2)^3=(x+2)^3(x+3)$]] |
Tekijöihin jakaminen muistikaavojen avulla
Muistikaavat
 Muistikaavojan avulla saadaan jaetuksi tekijöihin polynomilausekkeita, joissa ei esiinny kaikille termeille yhteistä tekijää. Muistikaavoja ovat:
Muistikaavojan avulla saadaan jaetuksi tekijöihin polynomilausekkeita, joissa ei esiinny kaikille termeille yhteistä tekijää. Muistikaavoja ovat: - "Summan neliö"
- "Erotuksen neliö"
- "Summan ja erotuksen tulo"
Esimerkki 2.
a) Jaa tekijöihin, eli esitä tulomuodossa lauseke [[$4x^2-81.$]]
| "Kahden termin neliöiden erotus on yhtä suuri kuin samojen termien summan ja erotuksen tulo." [[$A^2-B^2 =(A+B)(A-B)$]] |
Ratkaisu:
[[$4x^2-81 \\ = (2x)^2-9^2 \\ = (2x+9)(2x-9).$]]
b) Jaa tekijöihin, eli esitä tulomuodossa lauseke [[$ 25x^2-10x+1.$]]
| [[$A^2-2AB+B^2=(A-B)^2$]] |
Ratkaisu:
[[$ 25x^2-10x+1 \\ = (5x)^2 - 2\cdot 5x \cdot 1 + 1^2 \\ = (5x+1)^2 = (5x+1)(5x+1).$]]
c) Jaa tekijöihin, eli esitä tulomuodossa lauseke [[$ 9x^2+24x+16.$]]
| [[$A^2+2AB+B^2=(A+B)^2$]] |
Ratkaisu:
[[$9x^2+24x+16 \\ = (3x)^2+2 \cdot 3x \cdot 4 +4^2 \\ = (3x+4)^2 = (3x+4)(3x+4).$]]
Esimerkkejä muistikaavojen soveltamisesta
Toimintaohje
Tutki, voiko lauseketta muokata muotoon, jossa se muistuttaa auki laskettua binomin neliötä [[$A^2 \pm 2AB+B^2$]] tai kahden termin neliöiden erotusta [[$A^2-B^2$]].
Esimerkki 1.
|
|---|
[[$9x^2+6x+1\\=(3x)^2+6x + 1^2\\=\underbrace{(3x)^2}_{A^2}+2\cdot\underbrace{3x}_{A} \cdot \underbrace{1}_{B}+\underbrace{1^2}_{B^2}$]]Nähdään, että lauseke on muotoa [[$A^2+2AB+B^2$]], joten kyseessä on binomin neliö [[$(A+B)^2$]]: [[$(3x+1)^2$]] |
Vastaus: [[$9x^2+6x+1$]] jaettuna 1. asteen tekijöihin on [[$(3x+1)(3x+1)$]] |
Esimerkki 2.Jaa 1. asteen tekijöihin, eli esitä tulomuodossa lauseke [[$4x^2-20x+25$]]. |
|---|
[[$4x^2-20x+25\\=(2x)^2-20x + 5^2\\=\underbrace{(2x)^2}_{A^2}-2\cdot\underbrace{2x}_{A} \cdot \underbrace{5}_{B}+\underbrace{5^2}_{B^2}$]]Nähdään, että lauseke on muotoa [[$A^2-2AB+B^2$]], joten kyseessä on binomin neliö [[$(A-B)^2$]]: [[$(2x-5)^2$]] |
Vastaus: [[$4x^2-20x+25$]] jaettuna 1. asteen tekijöihin on [[$(2x-5)(2x-5)$]]. |
Esimerkki 3.Jaa 1. asteen tekijöihin, eli esitä tulomuodossa lauseke [[$16x^2-36$]]. |
|---|
[[$16x^2-36\\=\underbrace{(4x)^2}_{A^2}-\underbrace{6^2}_{B^2}$]]Nähdään, että lauseke on muotoa [[$A^2-B^2$]], [[$(4x+6)(4x-6)$]] |
Vastaus: [[$16x^2-36$]] jaettuna 1. asteen tekijöihin on [[$(4x+6)(4x-6)$]]. |
Polynomin jakaminen tekijöihin nollakohtien avulla
Polynomin jaollisuus
Jos [[$x_1$]] on polynomin nollakohta, niin silloin [[$(x-x_1)$]] on polynomin tekijä. Kääntäen pätee myös, että jos polynomilla on tekijänä [[$(x-x_1)$]], niin silloin [[$x_1$]] on polynomin nollakohta.Jos polynomilla ei ole reaalilukujen joukossa yhtään nollakohtaa, sitä ei voida jakaa reaalilukutekijöihin ja sanotaan, että polynomi on jaoton.
Polynomin jakolause |
|---|
Jos [[$x_1$]] on polynomin nollakohta, niin [[$(x-x_1)$]] on polynomin tekijä. |
Seuraus:
Mikä tahansa polynomi
[[$P(x)=a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0, $]] voidaan kirjoittaa tulomuotoon:
[[$P(x)=a_n (x-x_1)(x-x_2)\dots(x-x_n)$]]
missä [[$\{ x_1, x_2, ..., x_n \} $]]ovat yhtälön [[$P(x)=0$]] ratkaisut, eli [[$P$]]:n nollakohdat ja [[$a_n$]] on korkeimman asteisen termin kerroin.
Esimerkki 1.
Määritä sellainen 3. asteen polynomi, jonka nollakohdat ovat:
[[$x=-2$]], [[$x=1$]] ja [[$x=3$]].
Ratkaisu:
Muodostetaan polynomin tulomuotoinen esitys nollakohtien avulla:
[[$P(x)=(x-(-2))(x-1)(x-3)$]]
Lasketaan sulut auki:
[[$\begin{align}&=(x+2)(x-1)(x-3)\\&=(x^2+x-2)(x-3)\\&=x^3-3x^2+x^2-3x-2x+6\\&=x^3-2x^2-5x+6\end{align}$]]
Vastaus:
Eräs 3. asteen polynomi, jonka nollakohdat ovat [[$x=-2$]], [[$x=1$]] ja [[$x=3$]] on [[$P(x)=x^3-2x^2-5x+6$]]
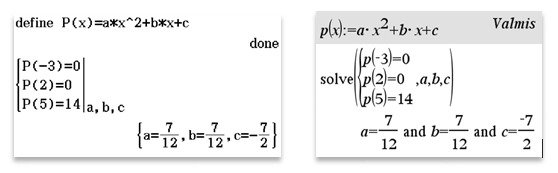
Esimerkki 2.
Määritä se toisen asteen polynomi,
jonka nollakohdat ovat [[$x_1=-3$]] ja [[$x_2=2$]]
ja [[$P(5)=14$]].
Ratkaisu:
Yleisen polynomien jakolauseen mukaan
[[$P(x)=a(x-x_1)(x-x_2),$]] missä [[$x_1$]] ja [[$x_2$]] ovat polynomin nollakohdat.
[[$\begin{align}P(x)&=a (x-(-3)) (x-2)\\&=a(x+3)(x-2)\\&=ax^2+ax-6a\end{align}$]]
Ratkaistaan [[$a$]] ehdosta [[$P(5)=14$]]
[[$\begin{align}P(5)&=14\\a(5+3)(5-2)&=14\\a&=\frac{14}{(5+3)(5-2)}\\a&=\frac{14}{24}=\frac{7}{12}\end{align}$]]
Kysytty polynomi on
[[$\begin{align}P(x)&=\frac{7}{12} (x+3) (x-2)\\&=\frac{7}{12}x^2+\frac{7}{12}x-\frac{7}{2}\end{align}$]]