mab7

441

$n’(t)=−2{,}1\cdot3t^2+37\cdot2t−155\cdot1+0=−6{,}3t+74t−155$

$−6{,}3t^2+74t−155=0$

$n(0)=−2{,}1⋅03+37⋅02−155⋅0+830=830$

$n(2{,}728\dots)=−2{,}1\cdot2{,}728\dots3+37\cdot2{,}728\dots2−155\cdot2{,}728\dots+830=639{,}879\dots\approx640$

$n(9{,}017\dots)=−2{,}1\cdot9{,}017\dots3+37\cdot9{,}017\dots2−155\cdot9{,}017\dots+830=901{,}106\dots\approx900$

$n\left(10\right)=−2{,}1\cdot103+37\cdot102−155\cdot10+830=880$

V: 640-900 lintua

0 kommenttia

411

$f'\left(x\right)=4\ joten\ ei\ nollakohtia$

$f(−3)=4\cdot(−3)+7=−12+7=−5$

$f(3)=4⋅3+7=12+7=19$

V:Suurin 19 ja pienin -5

$f′(x)=−3x^2+6x$

$-3x^2+6x=0$

$x=\frac{-6\ \pm\sqrt{6^2-4\cdot\left(-3\right)\cdot0}}{2\cdot\left(-3\right)}$

$\frac{-6\pm6}{-6}$

$x=0\ tai\ x=-2$

$f(−1)=−(−1)^3+3\cdot(−1)^2=−(−1)+3\cdot1=1+3=4$

$f(0)=−0^3+3\cdot0^2=0$

$f(2)=−2^3+3\cdot2^2=−8+3\cdot4=−8+12=4$

V: Suurin 4 ja pienin 0

0 kommenttia

402, 404, 410

402
a,

$2x+2=0$

$2x=-2$
$x=-1$

$f\left(-3\right)=\left(-3\right)^2+2\cdot\left(-3\right)=-3$
$f\left(-1\right)=\left(-1\right)^2+2\cdot\left(-1\right)-6=-7$
$f\left(2\right)=2^2+2\cdot2-6=2$

suurin arvo 2, pienin -7 välillä [-3,2]

0 kommenttia

moniste 5

A, B,

moniste 4

B, C

moniste 3

B ja C

moniste 2

A,D

1 moniste

A, C

337

a. oikein
b. väärin
c. väärin, 0
d. oikein

336

kasvava, kun x ≤ 3 eli ]−∞,3] ja vähenevä, kun x ≥ 3 eli [3,∞[

0 kommenttia

317

$-x^2+4x-3\ge0$

funktion nollakohdat:
$-x^2+4x-3=0$

$x=\frac{-4\pm\sqrt{4^2-4\cdot\left(-1\right)\cdot\left(-3\right)}}{2\cdot\left(-1\right)}=\frac{-4\pm\sqrt{4}}{-2}$
$x=\frac{-4+2}{-2}=1$

tai

$x=\frac{-4-2}{-2}=3$

vastaus, $1\le x\le3$

TAI valitaan kohdat nollakohtien rajaamilta lukusuoran väleiltä ja lasketaan niissä funktion arvot

Funktion g(x)=x^2-2x+3 nollakohdat

$x^2-2x+3=0$
$x=\frac{-\left(-2\right)\pm\sqrt{\left(-2\right)^2-4\cdot1\cdot3}}{2\cdot1}$

$=\ \frac{2\pm\sqrt{-8}}{2}$

ei nollakohtia

0 kommenttia

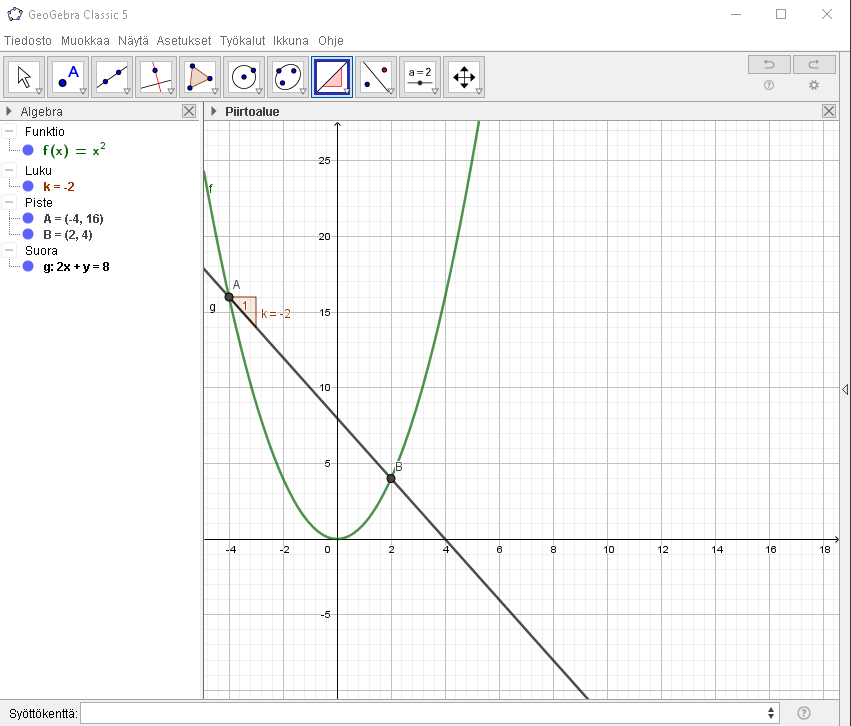
262

tangentin kulmakerroin :

$f'\left(4\right)$
eli

$f'\left(x\right)=-2x+2$

$f'\left(4\right)=-2\cdot4+2=-8+2=-6$

lasketaan funktion arvo kohdassa x = 4

$f\left(4\right)=4^2+2\cdot4+1=-16+8+1=-7$

muodostetaan suoralle yhtälö

$-6\cdot4+b=-7$

$b=-7+24=17$
tangentin yhtälö $y=-6x+17$

0 kommenttia

238

238 a

$f\left(3\right)\ =\ 3^2-5\cdot3+4=9-15+4=-2$

$f'\left(x\right)=2x-5$

$f'\left(3\right)=2\cdot3-5=6-5=1$

0 kommenttia

243

a,
$-6x+12$
$f'\left(0\right)=12$

b,
$-6x+12=0$
$12=6x\ \ :6$
$x=2$

0 kommenttia

238

a.
$3^2-5\cdot3+4$
$=9-15+4$
$=-2$

b.
$f'\left(x\right)=2x-5$

c,
$2\cdot3-5=1$

0 kommenttia

215

a,
$D(6x^5+4x^3+3x^2+x)$
$=6⋅5x^4+4⋅3x^2+3⋅2x+1$
$=30x^4+12x^2+6x+1$

b,
$D\left(\frac{3}{4}x^4+\frac{4}{3}x^3-\frac{1}{2}x^2+7\right)$
$=\frac{3}{4}\cdot4x^3+\frac{4}{3}\cdot3x^2-\frac{1}{2}\cdot2x+0$
$=3x^3+4x^2-x$

c,
$\frac{1}{3}\cdot7x^6+\frac{1}{2}+0=\frac{7}{3}x^6+\frac{1}{2}$
$=\frac{7}{3}x^6+\frac{1}{2}$

0 kommenttia

209

a, $11x-7x^2+9+2x=-7x^2+13x+9$
$g'\left(x\right)=-14x+13$

b, $4x^2-4x^4-2x+2x^3$
$=-4x^4+2x^3+4x^2-2x$
$g'\left(x\right)=-16x^3+6x^2+8x-2$

c, $x2-4x+4\ ja\ g'\left(x\right)\ =\ \ 2x-4$

0 kommenttia

derivointisetti

a, $f\left(x\right)\ =\ 2x\ -\left(x+7\right)$
$=\ 2x\ -x\ -7$
$=x-7$
$f'\left(x\right)\ =\ 1$

b, $g\left(x\right)\ =\ \left(x-2\right)\left(x+3\right)$
$x^2+3x-2x-6$
$x^2+x-6$
$g'\left(x\right)=2x+1$

c, $h\left(x\right)\ =\ \frac{4x^3+3x^2}{3}=\frac{4}{3}x^3+x^2$
$h'\left(x\right)=\frac{4}{3}\cdot3x^2+2x=4x^2+2x$