2.3 Nesteen paine ja kokonaispaine
Paine nesteessä
 Nesteen painon aiheuttamaa painetta kutsutaan hydrostaattiseksi paineeksi. Hydrostaattinen paine kasvaa sen myötä, mitä suurempi paino tarkastelupisteen yläpuolella on. Täten nesteen paine on sitä suurempi, mitä syvemmällä ollaan. Paineen kasvun huomaa jo parin metrin syvyydellä vedessä. Laskeuduttaessa kilometrien syvyyteen tarvitaan vahva suojakuori pitämään sukellusveneen muoto ennallaan.
Nesteen painon aiheuttamaa painetta kutsutaan hydrostaattiseksi paineeksi. Hydrostaattinen paine kasvaa sen myötä, mitä suurempi paino tarkastelupisteen yläpuolella on. Täten nesteen paine on sitä suurempi, mitä syvemmällä ollaan. Paineen kasvun huomaa jo parin metrin syvyydellä vedessä. Laskeuduttaessa kilometrien syvyyteen tarvitaan vahva suojakuori pitämään sukellusveneen muoto ennallaan.
Mitataan paineanturilla paine eri syvyydellä vedessä. Piirretään mittaustuloksista kuvaaja, jossa vaaka-akselilla on syvyys ja pystyakselilla paine, eli kyseessä on [[$(h,p)$]] -koordinaatisto.
Toistetaan mittaus syvemmässä astiassa ja tehdään se veden lisäksi myös etanolille. Piirretään kuvaajat samaan koordinaatistoon.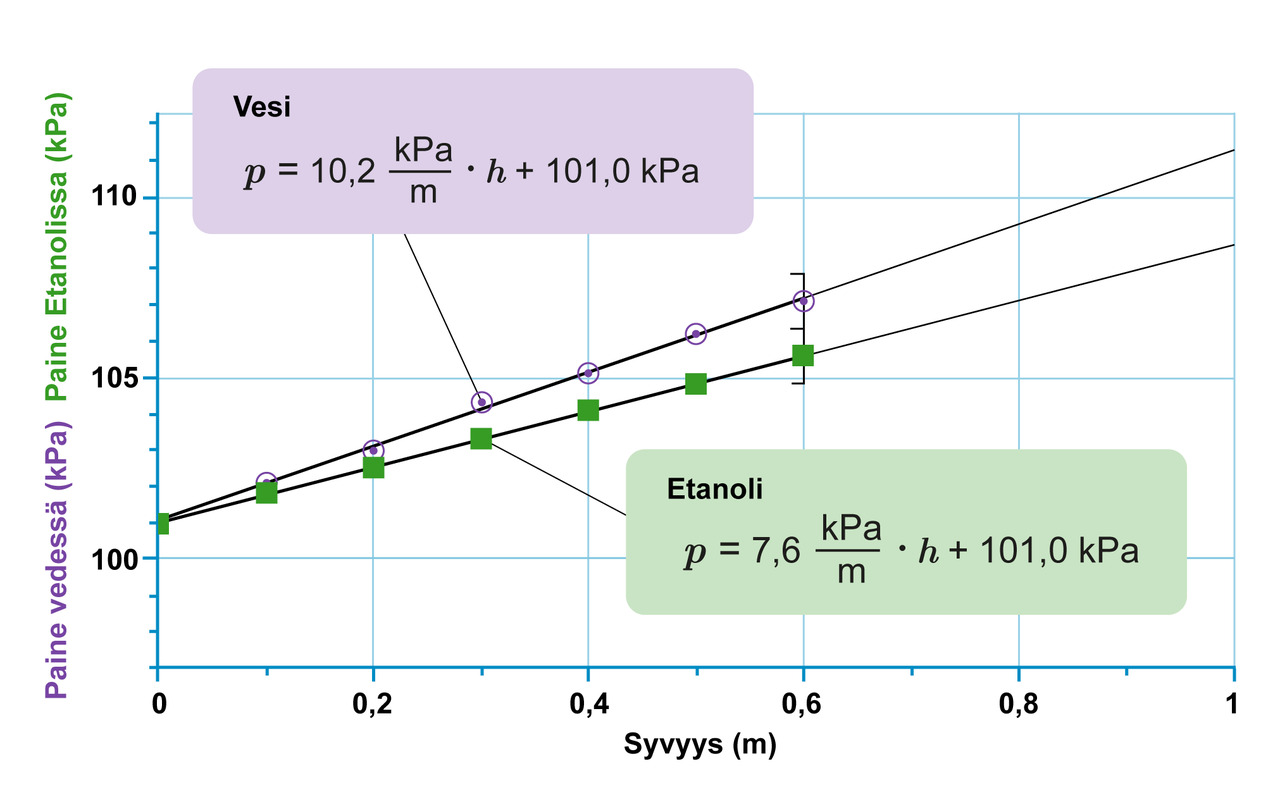
Mittaustulokset:
Hydrostaattinen paine vedessä ja etanolissa.cmbl (Logger Pro)
Hydrostaattinen paine vedessä ja etanolissa.ods (LibreOffice Calc)
Hydrostaattinen paine vedessä ja etanolissa.cap (Capstone)
Paineen kuvaajat ovat suoria, jotka leikkaavat pystyakselin samassa kohdassa. Niiden yhtälöt ovat muotoa [[$p=kh+b$]], missä k on suoran kulmakerroin ja b vakiotermi. Vakiotermi b ilmaisee suorien leikkauspisteen pystyakselin kanssa eli paineen suuruuden syvyydellä nolla. Tällöin ollaan nesteen pinnalla, jossa paine on normaalin ilmanpaineen suuruinen, noin 101 kPa. Kulmakertoimet ovat erilaisia, koska nesteiden ominaisuudet poikkeavat toisistaan. Seuraavassa kappaleessa tutkitaan, mitkä nesteen ominaisuudet vaikuttavat sen aiheuttaman paineen suuruuteen.
Hydrostaattinen paine ja kokonaispaine
 Tarkastellaan paineen suuruutta syvyydellä h. Tarkastelukohdan yläpuolella on nestepatsas, jolla on paino G. Paineen määrittämiseksi on rajattava nestepatsaalle pinta-ala A, johon painon vaikutus kohdistuu.
Tarkastellaan paineen suuruutta syvyydellä h. Tarkastelukohdan yläpuolella on nestepatsas, jolla on paino G. Paineen määrittämiseksi on rajattava nestepatsaalle pinta-ala A, johon painon vaikutus kohdistuu.
Nestepatsaan paino on
[[$\quad G=mg,$]]
missä m on nestepatsaan massa ja g on putoamiskiihtyvyys.
Nestepatsaan aiheuttama paine on
[[$\quad p=\dfrac{F}{A}=\dfrac{G}{A}=\dfrac{mg}{A}$]].
Edellä johdetussa lausekkeessa nestepatsaan massa ja pinta-ala ovat hankalasti määritettäviä suureita. Ne ovat tilannekohtaisia, joten paineen lauseke on kirjoitettava toiseen muotoon.
Nesteen tiheys yhdistää massan ja tilavuuden V toisiinsa. Tilavuus puolestaan on korkeuden ja pohjan pinta-alan tulo.
[[$\quad \rho = \dfrac{m}{V}=\dfrac{m}{Ah}$]]
Massalle saadaan lauseke [[$ m=\rho Ah$]].
Sijoittamalla tämä paineen lausekkeeseen saadaan
[[$\quad p=\dfrac{\rho Ahg}{A}=\rho gh.$]]
Nyt nesteessä vallitsevan paineen lauseke on saatu johdettua sopivaan muotoon, koska tiheys on nesteelle ominainen suure, putoamiskiihtyvyys on luonnonvakio ja korkeus on helposti mitattava suure.
Hydrostaattisen paineen lauseke ennustaa paineen kasvavan lineaarisesti mentäessä syvemmälle, mikä on yhtäpitävää edellisessä kappaleessa tehtyjen havaintojen kanssa. Paineen kuvaajien kulmakertoimet riippuvat nesteen tiheydestä. Veden tapauksessa kulmakerroin oli suurempi kuin etanolin tapauksessa. Vedessä paine kasvaa syvemmälle mentäessä voimakkaammin kuin etanolissa, koska vedellä on suurempi tiheys kuin etanolilla.
Nesteen paineen riippuvuus korkeudesta poikkeaa ilmanpaineen korkeusriippuvuudesta. Ilma voi puristua kokoon, minkä takia alhaalla oleva ilma on tiheämpää kuin ylhäällä oleva. Laskeuduttaessa ilmakehässä yläpuolella olevan ilman määrä ja paine kasvavat sitä nopeammin, mitä alempana ollaan. Neste ei juuri puristu kokoon, joten syvemmälle mentäessä yläpuolella olevan nesteen määrä kasvaa tasaisesti.
Paineanturit mittaavat nesteessä kokonaispainetta. Kokonaispaineeseen vaikuttavat nesteen paine sekä nesteen yläpuolella vallitseva ilmanpaine. Ellei erikseen mainita, nestepintaan kohdistuu normaali ilmanpaine, jolloin kokonaispaine on normaalin ilmanpaineen ja hydrostaattisen paineen summa.
Hydrostaattinen paine
Neste aiheuttaa paineen [[$p_{\text{h}}$]] syvyydellä [[$h$]], jonka tiheys on [[$\rho$]],
[[$\quad p_{\text{h}}=\rho g h,$]]
missä [[$g$]] on putoamiskiihtyvyys ja [[$\rho$]] on nesteen tiheys.
Kokonaispaine
Kokonaispaine nesteessä aiheutuu hydrostaattisesta paineesta [[$p_{\text{h}}$]] ja ilmanpaineesta [[$p_0$]].
[[$\quad p_{\text{kok}}=p_{\text{h}}+p_0=\rho g h+p_0$]]
Pysähdy pohtimaan
Esimerkit
Esimerkki 1
Esimerkki 2
Lasi täytetään vedellä ja kanneksi laitetaan ohut muovilevy. Miksi levy pysyy paikallaan ja vesi lasissa, kun lasi käännetään ylösalaisin?
Esimerkki 3

- Kuinka syvä vesikerros aiheuttaa ilmanpaineen suuruisen paineen?
- Laske sukeltajaan kohdistuva paine sukeltajan ollessa vesialtaassa 25 metrin syvyydessä. Vertaa ilmanpaineeseen.
