- osittain vanhan asian kertausta eli ympyrän pinta-alan laskemista

• ympyrän pinta-alaa varten pitää tietää vain ympyrän säde 
  • jos annetaan halkaisija, pitää siis tämä jakaa kahdella niin saadaan säde
  • jos annetaan ympyrän kehä, niin jakamalla piillä, saadaan halkaisija, josta päästään säteeseen
• ympyrän pinta-ala lasketaan siis 

​[[$$ Ala = \pi \cdot r^2 $$]]​

• • eli Ala = pii x säde^2

• viime kerran muistiinpanoissa on usea laskuesimerkki perustehtävissä, jossa lasketaan pinta-ala

- ne, jotka hakevat kiitettävää numeroa, kannattaa katsoa päivän uusia asia täöstä eteenpäin

• mites sitten saadaan selville säde (tai halkaisija), jos tiedetään pinta-ala?
  • tähän mennessä tehtävissä on tiedetty säde (tai halaksija) ja laskettu pinta-ala
• esim. Terassi on ympyränmuotoinen ja sen pinta-ala on 50 m^2. Kuinka paljon on terassin halkaisija? 

• • nyt tiedetään, että ympyrän pinta-ala on 50m^2 ja pinta-alan kaavasta saadaan selville säde. Tämän jälkene saadaan sitten halkaisija kertomalla säde kahdella. Muodostetaan yhtälö ja ratkaistaan yhtälöstä säde r. Yhtälössä pii:hän on luku eli noin 3,14 eli se on kerroin, joka saadaan "pois" jakamalla yhtälö pii:llä:

​[[$$ \begin {split}
 \pi \cdot r^2&=50&||:\pi \\
 r^2&=\frac{50}{\pi} \\
 r^2&=15,9&||\sqrt{} \\
 r&=\sqrt{15,9}&\\ r&=4& \end{split} $$]]​​

• • säde on siis 4,0 m, joten halkaisija on siis 8,0 m 

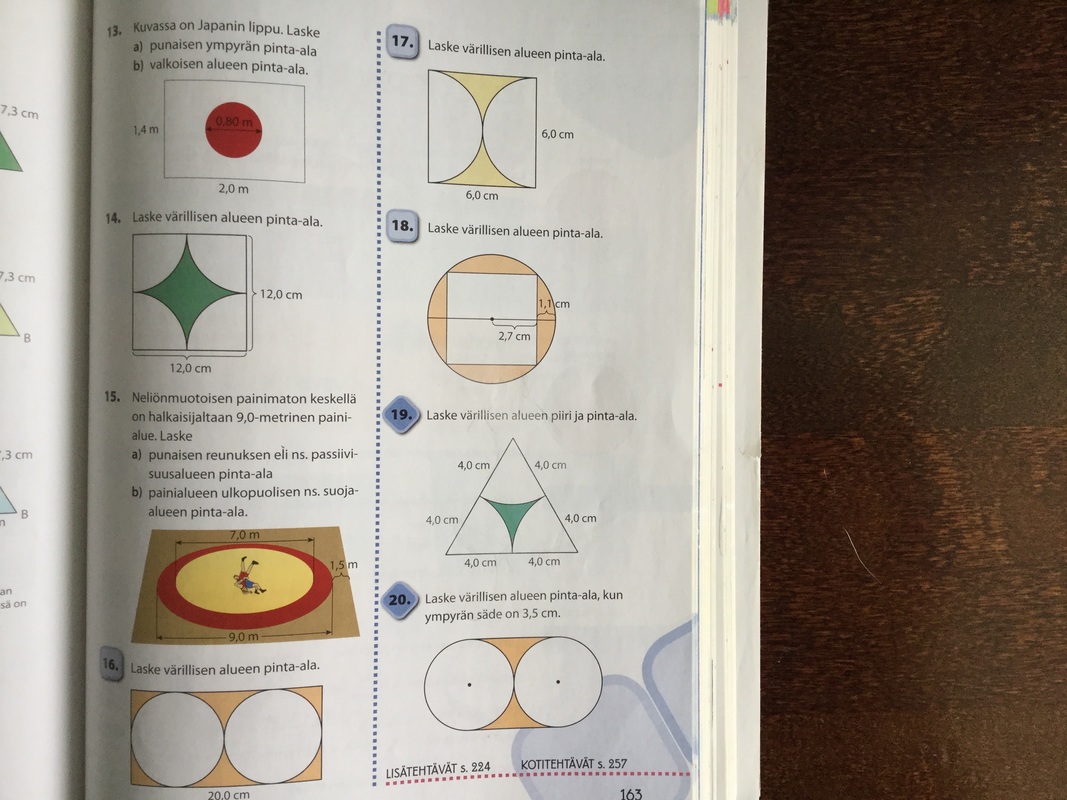
- perustehtävät 1, 2, 9, 13, 14, 16
- vet-tehtävät 11, 12, 17-20 (tarvitset t.19 Pythagoraan lausetta)