Esimerkkitilanteita
Huvipuistolaite
Huvipuistossa on pyörivä alusta (kuva alla). Sen pyörimisnopeus on 7,5 RPM.
a)
Alustalle asettuvan henkilön massa on 51 kg. Kuinka suuri kitkavoima tarvitaan pitämään paikallaan henkilöä, joka on 1,2 m:n etäisyydellä pyörivän alustan keskipisteestä?
b)
Miten henkilöä paikallaan pitävä kitkavoima muuttuu, kun hän siirtyy kauemmas keskipisteestä?
Ratkaisu
a)
Dynamiikan peruslain mukaan [[$ \Sigma \bar{F}=m\bar{a} $]]. Pysyäkseen ympyräradalla henkilöllä pitää olla ympyrärataehdon mukainen normaalikiihtyvyys: [[$a=a_n=\dfrac{v^2}{r}$]]. Tämän normaalikiihtyvyyden aiheuttaa henkilön ja alustan välinen kitkavoima.
[[$ \begin{align*} \quad \overline{F}_{\mu}&=m\overline{a} \\ \,\\ F_{\mu}&=ma_n \\ \,\\ F_{\mu}&=m\dfrac{v^2}{r} \\ \end{align*} $]]
Nopeuden [[$v$]] ja pyörimisnopeuden [[$n$]] välinen yhteys on [[$ v=\dfrac{2\pi r}{T}=2\pi r\cdot n $]]. Nyt voidaan laskea kitkavoiman suuruus pyörimisnopeuden avulla:
[[$ \begin{align} \quad F_{\mu}&=m\dfrac{(2\pi r \cdot n)^2}{r} \\\,\\&=m\cdot 4\pi^2 rn^2\end{align} $]]
Alkuarvot ovat [[$ m=51 \text{ kg}\text{ , } r=\text{1,2 m} \text{ ja } n=\text{7,5 RPM}=\text{0,125 kierrosta/s} $]].
Ratkaisuksi saadaan
[[$ \begin{align} \quad F_{\mu}&=51\text{ kg}\cdot4\pi^2\cdot \text{1,2 m}\cdot\left(\text{0,125 1/s}\right)^2 \\ \, \\ &=\text{37,7}\ldots \text{ N}\approx 38 \text{ N}\end{align} $]]
b)
Kitkavoiman lauseke johdettiin kohdassa a): [[$ F_{\mu}=m\cdot 4\pi^2 rn^2 $]]. Lausekkeesta huomataan, että kitkavoima on suoraan verrannollinen etäisyyteen pyörivän alustan keskipisteestä. Mitä kauemmas keskipisteestä siirrytään, sitä suurempi henkilöä paikallaan pitävän kitkavoiman on oltava.
Lumilautailija
 Lumilautailussa halfpipe-kourun säde on 4,2 m. Tarkastellaan tilannetta, jossa lumilautailija on juuri tulossa kourun vaakasuoralle osalle ympyrärataosalta. Lautailija etenee nopeudella 7,7 m/s.
Lumilautailussa halfpipe-kourun säde on 4,2 m. Tarkastellaan tilannetta, jossa lumilautailija on juuri tulossa kourun vaakasuoralle osalle ympyrärataosalta. Lautailija etenee nopeudella 7,7 m/s.
a)
Piirrä voimakuvio, josta ilmenee laskijaan kohdistuvan tukivoiman, painon ja normaalikiihtyvyyden suunnat. Liikettä vastustavia voimia ei huomioida.
b)
Kuinka moninkertainen pinnan tukivoima on painoon nähden?
Ratkaisu
a)
Lumilautailijaan vaikuttavat sekä paino [[$G$]], jonka suunta on alaspäin, että tukivoima [[$N$]], jonka suunta on ylöspäin. Normaalikiihtyvyyden [[$a_n$]] suunta on kohti radan keskipistettä, tukivoiman suuntaan. Näin ollen tukivoiman tulee olla painoa suurempi.
b)
Dynamiikan peruslain mukaan [[$\Sigma \bar{F}=m\bar{a}$]]. Koska lumilautailija on vielä ympyräradalla, kiihtyvyyden tulee olla ympyrärataehdon mukainen normaalikiihtyvyys [[$a_N=\dfrac{v^2}{r}$]]. Liikeyhtälöä voidaan muokata seuraavasti:
[[$ \begin{align*} \quad \overline{N}+\overline{G}&=m\overline{a} \\ \, \\ N-G&=ma_n \\ \, \\ N&=ma_n+mg = m(a_n+g) \\ \, \\ N&=m\left(\dfrac{v^2}{r}+g\right) \\ \end{align*} $]]
Lasketaan kysytty tukivoiman suhde painoon:
[[$ \begin{align*} \quad \dfrac{N}{G}&=\dfrac{m\left(\dfrac{v^2}{r}+g\right)}{mg} \\ \, \\ \dfrac{N}{G}&=\dfrac{\dfrac{v^2}{r}+g}{g} \\ \end{align*} $]]
Havaitaan, että lumilautailijan massa ei vaikuta asiaan. Sijoitetaan alkuarvot: [[$ v=\text{7,7 m/s} \text{ , } r=\text{4,2 m} \text{ ja } g=\text{9,81 m/s}^2 $]]. Ratkaisuksi saadaan
[[$ \begin{align} \quad \dfrac{N}{G}&=\dfrac{\dfrac{\left(\text{7,7 m/s}\right)^2}{\text{4,2 m}}+\text{9,81 m/s}^2}{\text{9,81 m/s}^2} \\ \, \\ &=\text{2,4390}\ldots \approx \text{2,4}\end{align} $]]
Pinnan tukivoima on 2,4-kertainen verrattuna painoon.
Lentävä porsas
Porsas pyörii ilmassa ympyräradalla. Lentävän porsaan massa on 190 g. Langan pituus on 1,3 m. Langan ja pystysuoran suunnan välinen kulma on 24 astetta.
a)
Laske videota käyttäen arvio porsaan normaalikiihtyvyydelle ja nopeudelle.
b)
Piirrä kuvio, josta ilmenee tilanteessa vaikuttavat voimat.
c)
Kuinka suuri on liikettä kiihdyttävä kokonaisvoima ja mitkä ovat tilanteessa vaikuttavien voimien suuruudet?
a)
Videolta määritetään
- porsaan kierrosajaksi [[$T = \mathrm{2,1 \ s}$]]
- Langan ja pystysuoran väliseksi kulmaksi 24 astetta. Tästä saadaan trigonometrialla radan säde, kun tiedetään langan pituus: [[$r=\text{1,3 m}\cdot\sin 22^\circ=\text{0,49 m}$]].
Porsaan vauhti vaikuttaa pysyvän vakiona. Nopeus saadaan laskettua tasaisen liikkeen mallilla, kun tiedetään kierrosaika ja radan säde.
[[$ \begin{align} \quad v&=\dfrac{s}{t} \\\, \\&=\dfrac{2\pi r}{T}\\\, \\&=\dfrac{2\pi\cdot \text{0,49 m}}{\text{2,3 s}}\\\, \\&= \text{1,46607}\ldots \textrm{m/s}\approx \text{1,5 m/s}\end{align} $]]
Normaalikiihtyvyys saadaan laskettua ympyrärataehdosta:
[[$ \begin{align} \quad a_n&=\dfrac{v^2}{r} \\ \, \\ &=\dfrac{\left(\text{ 1,4661 m/s}\right)^2}{\text{0,49 m}}\\ \, \\&= \text{4,3866}\ldots \textrm{m/s}^2\approx \text{4,4 m/s}^2\end{align} $]]
b)
Voimakuvio
[[$G= \text{paino}$]]
[[$T=\text{langan kappaleeseen kohdistama voima}$]]
c)
Dynamiikan peruslain mukaan [[$ \Sigma \bar{F}=m\bar{a}$]]. Tässä porsas on tasaisessa ympyrärataliikkeessä, joten kiihtyvyyden tulee olla normaalikiihtyvyys [[$a_n=\dfrac{v^2}{r}$]]. Tämä kiihtyvyys on voimakuviossa valituissa suunnissa [[$x$]]-suuntaan. [[$y$]]-suunnan kiihtyvyys on nolla, koska porsas ei liiku [[$y$]]-suunnassa. Kirjoitetaan liikeyhtälöt [[$x$]]- ja [[$y$]]-suunnissa.
[[$ \begin{cases} T_x=ma_n \\ T_y-G=0 \\ \end{cases} $]]
[[$ \begin{cases}T_x=ma_n \\ T_y-mg=0 \\ \end{cases} $]]
Liikettä kiihdyttävä kokonaisvoima on sama kuin langan jännitysvoiman x-komponentti, ja se saadaan ratkaistua ylemmästä yhtälöstä. Sijoitetaan alkuarvot [[$ m=\text{0,190 kg}$]] ja [[$a_n=\text{4,387}\ldots \textrm{m/s}^2 $]].
[[$ \begin{align} \quad T_x &= \text{0,190 kg}\cdot \text{4,387 m/s}^2 \\ \, \\ &=\text{0,83353 N}\approx \text{0,83 N}\end{align} $]]
Paino [[$ G=mg=\text{0,190 kg}\cdot \text{9,81 m/s}^2=\text{1,8639 N}\approx \text{1,9 N} $]]
Langan tukivoiman pystysuuntainen osa on [[$y$]]-suunnan liikeyhtälön mukaan yhtä suuri kuin paino: [[$ T_y=G $]]. Langan tukivoima yhteensä saadaan Pythagoraan lauseella:
[[$ \begin{align} \quad T&=\sqrt{T_x^2+T_y^2} \\ \, \\ &=\sqrt{\left(\text{0,834 N}\right)^2+\left(\text{1,86 N}\right)^2} \\ \, \\&=\text{2,03}\ldots \textrm{ N}\approx \text{2,0 N}\end{align} $]]
Auto ympyräradalla
Auto ajaa vaakasuoralla tiellä ympyränmuotoisessa kaarteessa, jonka ratasäde on 55 m. Auton nopeus on 78 km/h. Kuinka suuri kitkakerroin renkaiden ja tien välillä tulee olla, jotta auto pysyy radallaan?
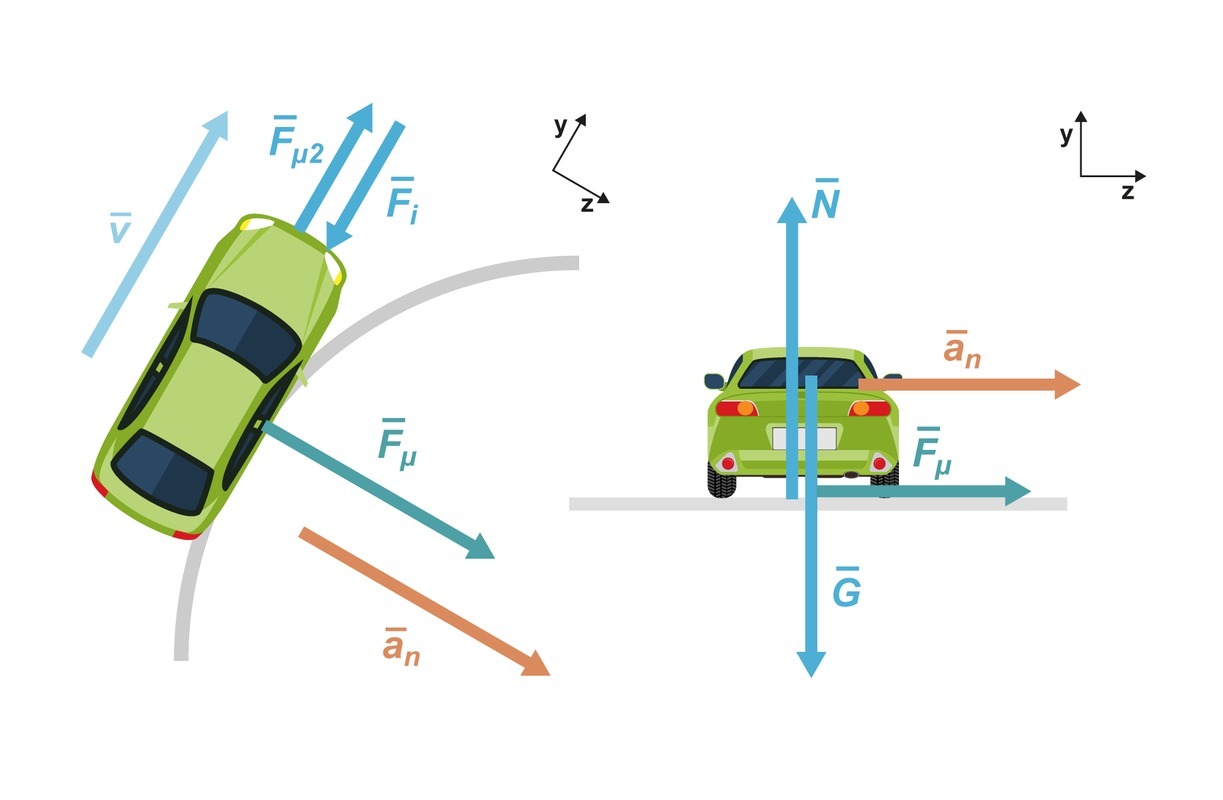
RatkaisuMääritetään aluksi autoon vaikuttavat voimat. Piirretään tilanteesta voimakuvio. Koska nopeus ei muutu, pysyy voimakuvio samanlaisena koko liikkeen ajan.
Vasen voimakuvio on piirretty ylhäältä ja oikea takaa siten, että ympyräradan keskipiste on oikealla. [[$G$]] on auton paino, ja [[$N$]] tienpinnan tukivoima. Jos oletetaan liikettä vastustavien voimien [[$F_\text{i}$]] olevan vähäisiä, liikkeen suunnassa ([[$x$]]-suunta) ei ole lainkaan voimia (koska ratanopeus on vakio) ja kitkavoima [[$F_\mu$]] suuntautuu pelkästään kohti ympyräradan keskipistettä pitäen auton ympyräradalla. Ympyrärataehdon mukaan normaalikiihtyvyys [[$a_n=\dfrac{v^2}{r}$]], mikä on [[$z$]]-suunnan kiihtyvyys. Auto ei liiku pystysuunnassa, joten y-suunnassa kiihtyvyys on nolla. Dynamiikan peruslain mukaan [[$\Sigma \bar{F}=m\bar{a}$]]. Kirjoitetaan liikeyhtälöt [[$z$]]- ja [[$y$]]-suunnassa:
[[$\quad \begin{cases} F_\mu=ma_n \\ N-G=0 \\ \end{cases}$]]
[[$\quad \begin{cases} N\mu=m\dfrac{v^2}{r} \\ N-mg=0 \\ \end{cases}$]]
Alemmasta yhtälöstä saadaan [[$N=mg$]]. Sijoitetaan tämä ylempään yhtälöön, ja ratkaistaan kitkakerroin. Tulokseksi saadaan:
[[$ \begin{align*} \quad mg\mu&=m\dfrac{v^2}{r} \\ \, \\ \mu & =\dfrac{v^2}{gr} \\ \, \\ & =\dfrac{\left(\dfrac{78}{\text{3,6}}\text{ m/s}\right)^2}{\text{9,81 m/s}^2\cdot 55\text{ m}} \\ \, \\ &=\text{0,870}\dotso\approx \text{0,87} \\ \end{align*} $]]
Kitkakertoimen on oltava vähintään 0,87. Tämä on varsin suuri kitkakerroin. Kun otetaan huomioon kaarteen jyrkkyys, auto ajaa vaarallisen suurella nopeudella.