2.2 Kvanttimekaniikka
Kvanttimekaniikan ominaispiirteitä
Kun sekä fotoneilla että hiukkasilla oli todettu olevan aalto- ja hiukkasluonne, syntyi tilausta teorialle, joka kuvaisi dualistisia hiukkasia sekä fotonien ja hiukkasten välistä vuorovaikutusta. Kehitettiin kvanttimekaniikan osa-alue. Kvanttimekaniikan teorialla on kaksi tukipilaria: fotonin käyttäytyminen energiapakettina ja hiukkasen mallintaminen Schrödingerin yhtälön avulla.
Kvantittuminen
Valosähköilmiössä havaittiin, että yksittäinen fotoni vuorovaikuttaa elektronin kanssa luovuttaen elektronille koko energiansa. Fotonille on ominaista, että se ei voi luovuttaa vain osaa energiastaan, vaan se katoaa vuorovaikutuksen tapahtuessa. Jos energia ei valosähköilmiössä riitä elektronin irrottamiseen, vuorovaikutusta ei tapahdu. Tämä on kvanttimekaniikan ensimmäinen perusperiaate: fotoni voi vuorovaikuttaa aineen kanssa vain syntymällä tai tuhoutumalla, ja samalla fotoni saa tai luovuttaa aineelle taajuuttaan vastaavan energian kokonaisuudessaan.
Schrödingerin yhtälö
Toinen perusperiaate on Schrödingerin yhtälö, matemaattinen malli aaltomaisten hiukkasten kuvaamiseen. Se on kvanttimekaniikassa samassa asemassa kuin Newtonin II laki klassisessa mekaniikassa. Muodoltaan se on lukiomatematiikan ulottumattomissa oleva differentiaaliyhtälö, jonka ratkaisuna saadaan hiukkasen sijainnin todennäköisyysjakauma ja jakauman aikakehitys tutkittavassa tilanteessa. Schrödingerin yhtälön avulla voidaan selvittää esim. elektronin tilaa sen ollessa vapaa tyhjässä avaruudessa tai sidottuna atomiytimen ympärillä.
Kuva: Oikealla on kuvattu elektronin sijainnin todennäköisyysjakauma perustilassa olevassa vetyatomissa. Värin voimakkuus kuvaa todennäköisyyttä löytää elektroni tietystä pisteestä. Musta piste keskellä on ydin.
Hiukkasen sijainnin todennäköisyysjakauman lisäksi Schrödingerin yhtälö antaa tuloksena hiukkasen energian. Kaikissa muissa tilanteissa paitsi tarkasteltaessa yksittäistä hiukkasta tyhjässä avaruudessa yhtälö tuottaa ratkaisuna vain tiettyjä energian arvoja. Sanotaan, että hiukkasen energia on kvantittunut. Sillä on pienin mahdollinen arvo, toiseksi pienin, jne. Energian kvantittuminen ilmenee monissa käytännön tilanteissa. Esimerkiksi ensimmäisessä luvussa esitellyt viivaspektrit selittyvät atomiytimen ympärillä olevan elektronin energian kvantittumisella.
Schrödingerin yhtälöllä on matemaattinen ominaisuus, jonka mukaan mikä tahansa sen yksittäisten ratkaisujen summa on myös yhtälön ratkaisu. Jos hiukkanen voi yhtälön mukaan olla energiatilassa [[$E_n$]] tai [[$E_m$]], se voi myös olla näissä kahdessa energiatilassa yhtä aikaa. Tilanne ei muutu, vaikka tiloja olisi kuinka monta. Kvanttimekaniikan hiukkanen voi olla vaikka 176 paikassa samanaikaisesti tai sillä voi olla 35 eri energiaa yhtä aikaa. Tilannetta, jossa hiukkasen jollain ominaisuudella on useita arvoja samanaikaisesti, kutsutaan superpositiotilaksi.
Superpositiotiloja ei havaita arjessa. Tämä selittyy sillä, että Schrödingerin yhtälön mukaan superpositiotila "romahtaa" vuorovaikutustapahtumassa johonkin yksittäiseen arvoon. Jos superpositiotilan yrittää havaita jollain mittalaitteella, mittarin ja mitattavan systeemin välillä on pakko olla vuorovaikutus. Näin mittaaminen "romauttaa" aina superpositiotilan johonkin arvoon, joka on mittaustulos. Tulosta ei voi tietää etukäteen, Schrödingerin yhtälö kertoo ainoastaan eri vaihtoehtojen todennäköisyydet. Tämä on keskeinen ero klassiseen fysiikkaan, jossa Newtonin lait, gravitaatiolaki ja Coulombin laki ennustavat tulevaisuuden täsmällisesti, kun alkutilanne tunnetaan tarkasti. Kvanttimekaniikassa mitään ei voida tietää tarkasti. Hiukkasen tarkan paikan sijaan käytössä on sijainnin todennäköisyysjakauma, ja kvantittuneille suureille tiedetään vain eri mittaustulosvaihtoehtojen todennäköisyydet.
Kvanttimekaniikkaa ei kuitenkaan tarvita mallintamaan makroskooppisia kappaleita. Mitä suuremmista hiukkasista on kyse, sitä hankalampi niiden on havaita käyttäytyvän kvanttimekaanisesti. Makroskooppisten kappaleiden tulevaisuuden mallintamiseen riittää klassinen fysiikka, koska ne ovat jatkuvasti vuorovaikutuksessa useiden muiden kappaleiden kanssa. Niillä ei ole pitkäaikaista superpositiotilaa, eikä siten arkikokemuksen vastaisia kvantti-ilmiöitä. Kvanttimekaniikka on kuitenkin välttämätöntä, jotta ymmärretään lyhytaikaisia hiukkasmaailman ilmiöitä.
Esimerkkitilanne: hiukkanen laatikossa
Energian kvantittuminen on keskeinen kvanttimekaniikan ominaisuus. 
Seuraava esimerkki havainnollistaa hiukkasen ominaisuuksien kvantittumista. Tarkastellaan hiukkasta tyhjässä avaruudessa, joka on rajattu eräänlaiseksi laatikoksi. Hiukkanen pääsee liikkumaan laatikon sisällä vapaasti, mutta ei sieltä ulos. Tilanne voisi olla approksimaatio elektronille puolijohdemateriaalissa, joka on rajattu ympäriltä eristeellä. Käytännössä malli on hyvin karkea sovellettavaksi.
Vaikka hiukkasen tila ratkaistaan kvanttimekaniikassa Schrödingerin yhtälön avulla, tällaisessa yksinkertaisessa tilanteessa Schrödingerin yhtälöä ei tarvita, koska ratkaisut voidaan päätellä. Laatikon sisällä hiukkanen käyttäytyy kuin tyhjässä avaruudessa: se on häiritsemätön aalto. Jos hiukkanen ei voi mitenkään päästä laatikosta ulos, aallon täytyy "päättyä" laatikon reunaan. Tilanne on samankaltainen kuin seisova aaltoliike, joka syntyy molemmista päistä kiinnitettyyn naruun. Näin ollen, jos laatikon leveys on [[$L$]], laatikkoon on mahduttava kokonainen määrä puolikkaita aaltoja. Laatikko ja neljä pisintä mahdollista aallonpituutta on havainnollistettu oikealla olevassa kuvassa. Aallot kuvaavat hiukkasen mahdollisia tiloja laatikossa.
Laatikon leveyden [[$L$]] on siis oltava kokonaisluku kertaa puolikas aallonpituus:
[[$L=n\dfrac{\lambda}{2} \Rightarrow \lambda=\dfrac{2L}{n}$]].
Sijoittamalla aallonpituuden lauseke hiukkasen de Broglien aallonpituuteen [[$\lambda=\frac{h}{p}$]] saadaan yhtälö
[[$\dfrac{2L}{n}=\dfrac{h}{p} \Rightarrow p=\dfrac{nh}{2L}$]].
Liikemäärän ja liike-energian välinen yhteys on
[[$E_\text{K}=\dfrac{p^2}{2m}$]].
Energialle saadaan lauseke
[[$E_\text{K}=\dfrac{\left(\dfrac{nh}{2L}\right)^2}{2m}= n^2\dfrac{h^2}{8L^2m}$]].
Lausekkeesta ilmenee, että energian täytyy olla energiatilan järjestysluvun [[$n=1,2,3,\ldots$]] neliö kertaa [[$\dfrac{h^2}{8L^2m}$]].
Tämä tarkoittaa, että energia on kvantittunut samoin kuin liikemäärä. Jos hiukkasen energiaa halutaan lisätä, siihen täytyy tuoda juuri sopiva energiamäärä. Jos energian lisäys tapahtuu absorboimalla fotoni, fotonin energian ja siten taajuuden pitää olla juuri sopiva. Tämä periaate pätee myös atomin ympärillä olevalle elektronille, jonka energiatiloja ei kuitenkaan pystytä johtamaan lukiomatematiikalla. Seuraavassa luvussa käsitellään elektronin energian kvantittumisen ilmenemistä, kun se on sidottu atomiytimen ympärille, ja miten energian kvantittuminen aiheuttaa alkuaineiden viivaspektrit.
Erilaisia kvantti-ilmiöitä
Tunneloituminen
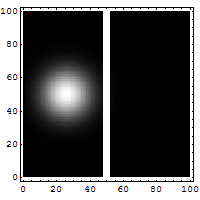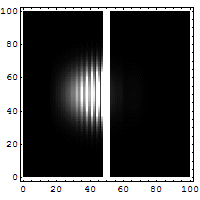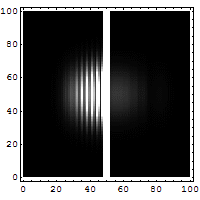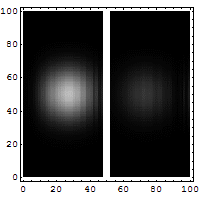
Tunneloituminen on ilmiö, jossa hiukkanen voi siirtyä läpi alueen, jolla liikkuminen ei klassisen mekaniikan mukaan olisi mahdollista. Tunneloitumisilmiö perustuu olettamukseen, että hiukkasella ei ole täsmällistä paikkaa, vaan sijainti esitetään todennäköisyysjakaumana. Jos klassisessa mielessä kielletyn alueen leveys on pieni, Schrödingerin yhtälön ratkaisuna tuleva todennäköisyysjakauma jatkuu sen toisella puolella. Oheisessa simulaatiossa elektroni törmää ohueen seinämään, josta sen ei klassisen fysiikan mukaan pitäisi päästä läpi. Elektronin sijainnin todennäköisyysjakauma on esitetty kirkkausvaihteluna: mitä kirkkaampi kohta, sitä todennäköisemmin siinä on elektroni. Himmeä pallo kulkee seinästä läpi ja kirkas heijastuu, eli elektroni tunneloituu pienellä todennäköisyydellä seinän läpi.
Arkipäiväinen tunneloitumista hyödyntävä sovellus ovat flash-muistit (muistitikut, SSD-levyt, ...). Niissä 
elektroneja voidaan varastoida eristekalvojen taakse kiihdyttämällä elektroneja jännitteen luomalla sähkökentällä kalvoa kohti. Riittävällä jännitteellä kiihdytetyt elektronit tunneloituvat eristekalvon taakse ja pysyvät siellä myös kytkettäessä kenttä pois päältä. Luettaessa muistia yksittäinen elektronisäiliö on nolla tai ykkönen sen mukaan, onko siellä elektroneja vai ei. Tunneloitumista hyödynnetään myös alle nanometrien luokkaa olevien rakenteiden kuvantamisessa. Laite on tunnelointimikroskooppi.
Video: Tunnelointimikroskoopin toimintaperiaate (La Physique Autrement)
Lomittuminen
Lomittuminen on kvantti-ilmiö, jossa kaksi systeemiä ovat kytkeytyneet toisiinsa, eikä kummankaan tilaa voi kuvailla toisesta riippumattomalla tavalla. Kun yhden lomittuneen systeemin tilaa tutkitaan, toisen tila muuttuu välittömästi. Tarkastellaan esimerkkinä tilannetta, jossa hiukkanen pomppii edestakaisin laatikossa. Laatikko jaetaan satunnaisella hetkellä kahteen osaan. Hiukkanen jää oikealle tai vasemmalle puoliskolle. Jos puoliskot nyt erotetaan, ne ovat lomittuneet. Alkutilanteessa kummassakin puoliskossa on hiukkanen ja ei ole hiukkasta. Jos nyt oikeaa puoliskoa tutkitaan ja havaitaan hiukkasen olevan siellä, vasemman puoliskon tila on myös tiedossa: on selvää, että siellä ei ole hiukkasta. Vasemman puoliskon tila ei ollut riippumaton oikeasta. Vasemman puoliskon tila muuttuu välittömästi, kun oikean puoliskon tilaa tutkitaan. Tämä tapahtuu riippumatta siitä, kuinka kaukana puoliskot ovat toisistaan.
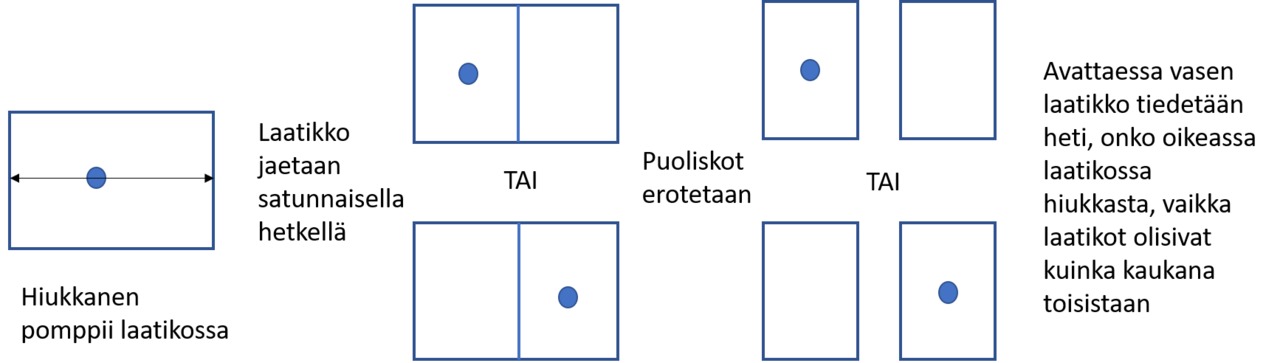
Tyypillinen lomittunut systeemi on kaksi alkeishiukkasta, esim. elektronipari, tai kaksi fotonia. Lomittuminen purkautuu mitattaessa jommankumman lomittuneen hiukkasen tila. Siksi lomittuminen rikkoutuu helposti vuorovaikutusten takia. Muiden kvantti-ilmiöiden tapaan lomittumista on siten hankala havaita makroskooppisilla hiukkasilla, koska niitä on vaikea täysin eristää vuorovaikutukselta ympäristön kanssa. Aalto-yliopistossa on kuitenkin onnistuttu todentamaan v. 2018 myös lähes makroskooppisten hiukkasten lomittuminen.
Einsteinin ennustama haamuvuorovaikutus (Aalto-yliopisto)
Yksi lomittumisen hyötykäyttö on herkkien kohteiden kuvaaminen. Kuvattavaan kohteeseen lähetetään matalaenergiaisia fotoneja, jotka ovat lomittuneet kameralle menevien korkeaenergiaisten fotonien kanssa. Kuva tulee tällöin otettua heti fotonien osuessa kohteeseen, ei vasta kohteesta sironneiden fotonien saapuessa takaisin kameraan. Lisäksi lomittuminen voidaan toteuttaa niin, että kameraan saapuvat fotonit ovat korkeaenergiaisia ja tulevat helposti havaittua kennolla, kun taas kuvattavaan näytteeseen osuvat fotonit ovat matalaenergiaisia, eivätkä vaurioita sitä. Tekniikka on hiljalleen leviämässä laajempaan käyttöön esim. valoherkkien biologisten näytteiden kuvaamisessa.
Lomittuneilla fotoneilla valokuvaaminen (Nature.com)
Lukuisat sovellukset pohjaavat kvantti-ilmiöihin. Jo lähitulevaisuudessa yksi merkittävä sovellus voi olla *kvanttitietokone.
Esimerkkejä
Esimerkki 1
Selitä lyhyesti seuraavat asiat:
a) superpositiotila ja sen romahtaminen
b) sijainnin todennäköisyysjakauma
c) energian kvantittuminen.
