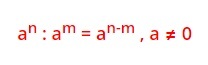2. Potenssilaskenta
2.1 Potenssi
Potenssimerkintä on tapa esittää kertolaskuja yksinkertaisemmin. Potenssien laskusääntöjen avulla voidaan laskea suuriakin kertolaskuja nopeammin.
Potenssimerkinnässä eksponentti kertoo kuinka monta kertaa kantaluku kerrotaan itsensä kanssa.
Määritelmä:
Yleisesti olkoot n positiivinen kokonaisluku (n = 1, 2, 3, ...).
Kantaluvun a n:s potenssi tarkoittaa tuloa an = a · a · a · ... · a · a, missä kantalukua kerrotaan n kertaa itsensä kanssa.
Esimerkki 1.
a) 23 = 2 · 2 · 2 = 8
b) (-2)3 = (-2) · (-2) · (-2) = -8 Huomaa ero, mikäli kantaluku on negatiivinen!
c) -23 = -2 · 2 · 2 = -8
Kantaluku on syytä merkitä (aina) sulkuihin. Edellisen esimerkin kohdassa b kantalukuna on -2, mutta kohdassa c kantalukuna on 2.
Potenssimerkinnässä eksponentti kertoo kuinka monta kertaa kantaluku kerrotaan itsensä kanssa.
Määritelmä:
Yleisesti olkoot n positiivinen kokonaisluku (n = 1, 2, 3, ...).
Kantaluvun a n:s potenssi tarkoittaa tuloa an = a · a · a · ... · a · a, missä kantalukua kerrotaan n kertaa itsensä kanssa.
Esimerkki 1.
a) 23 = 2 · 2 · 2 = 8
b) (-2)3 = (-2) · (-2) · (-2) = -8 Huomaa ero, mikäli kantaluku on negatiivinen!
c) -23 = -2 · 2 · 2 = -8
Kantaluku on syytä merkitä (aina) sulkuihin. Edellisen esimerkin kohdassa b kantalukuna on -2, mutta kohdassa c kantalukuna on 2.
2.2. Potenssien laskusäännöt
1) samankantaisen potenssien tulo
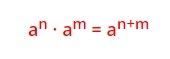
eli samankantaisten eksponenttien kertolaskussa kantaluku ei muutu, mutta eksponentit summataan yhteen.
Esimerkki 1.
a) x3 · x5 = x3+5 = x8
b) b4 · b-6 = b4+(-6) = b4-6 = b-2 (huomaa, että potenssi ollessa negatiivinen summa muuttuu erotukseski)
-------------------------------------------------------------------------------------------------------------------------------------------
2) samankantaisten potenssien osamäärä
eli samankantaisten eksponenttien kertolaskussa kantaluku ei muutu, mutta eksponentit vähennetään toisistaan (jaettavan eksponentti ensin). Jakolasku kannattaa aina esittää murtolukumuodossa.
Esimerkki 2.
a) x5 : x2 = x5 - 2 = x3
b) b4 : b-6 = b4-(-6) = b4 + 6 = b10 (jos jakajan potenssi on negatiivinen erotus muuttuu summaksi)
-------------------------------------------------------------------------------------------------------------------------------------------
3) tulon potenssi tulon potenssissa kaikki kerrottavat korotetaan erikseen merkittyyn potenssiin.
Esimerkki 3.
(2xy)5 =25x5y5 = 32x5y5
-------------------------------------------------------------------------------------------------------------------------------------------
4) osamäärän potenssi
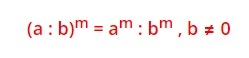
osamäärän potenssissa sekä jaettava että jakaja korotetaan erikseen merkittyyn potenssiin. Osamäärä kannattaa merkitä murtolukumuodossa, mikä helpottaa osamäärän tulkintaan.
Esimerkki 4.
(2x : 3y)3 = (2x)3 : (3y)3 = 8x3 : 27y3
-------------------------------------------------------------------------------------------------------------------------------------------
5) potenssin potenssi
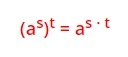
Potenssin korotus potenssiin tarkoittaa potenssien kertolaskua, mikäli potenssien välissä on sulkumerkintä. Mikäli sulkua ei ole, laskea potenssin potenssi normaalina potenssilaskuna.
Esimerkki 5.
(2x2)3 = 23x2 · 3 = 8x6
tai (2x2)3 = (2x2)(2x2)(2x2) = 2 · 2 · 2 · x2 · x2
-------------------------------------------------------------------------------------------------------------------------------------------
6) nolla eksponenttina
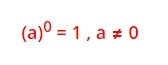
Luku potenssiin nolla on aina yksi, mikäli kantaluku on eri suuri kuin nolla. Tuloksen voi osoittaa useammallakin tavalla:
2 : 2 = 21 : 21 = 21 - 1 = 20 = 1 (yleensä todistus tehdään mille tahansa kantaluvulle a ≠ 0)
a · (1 : a) = a1 · a-1 = a1 + (-1) = a0 = 1 (luvun ja sen käänteisluvun tulo on aina 1)
-------------------------------------------------------------------------------------------------------------------------------------------
7) negatiivinen eksponentti
Negatiivinen eksponentti muutetaan positiivikseksi ja samalla kantaluku vaihdetaan käänteisluvuksi. Kantaluku kannattaa esittää murtolukuna ja sulkeiden sisällä.
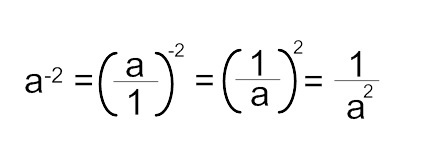
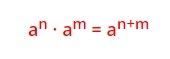
eli samankantaisten eksponenttien kertolaskussa kantaluku ei muutu, mutta eksponentit summataan yhteen.
Esimerkki 1.
a) x3 · x5 = x3+5 = x8
b) b4 · b-6 = b4+(-6) = b4-6 = b-2 (huomaa, että potenssi ollessa negatiivinen summa muuttuu erotukseski)
-------------------------------------------------------------------------------------------------------------------------------------------
2) samankantaisten potenssien osamäärä
eli samankantaisten eksponenttien kertolaskussa kantaluku ei muutu, mutta eksponentit vähennetään toisistaan (jaettavan eksponentti ensin). Jakolasku kannattaa aina esittää murtolukumuodossa.
Esimerkki 2.
a) x5 : x2 = x5 - 2 = x3
b) b4 : b-6 = b4-(-6) = b4 + 6 = b10 (jos jakajan potenssi on negatiivinen erotus muuttuu summaksi)
-------------------------------------------------------------------------------------------------------------------------------------------
3) tulon potenssi tulon potenssissa kaikki kerrottavat korotetaan erikseen merkittyyn potenssiin.
Esimerkki 3.
(2xy)5 =25x5y5 = 32x5y5
-------------------------------------------------------------------------------------------------------------------------------------------
4) osamäärän potenssi
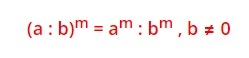
osamäärän potenssissa sekä jaettava että jakaja korotetaan erikseen merkittyyn potenssiin. Osamäärä kannattaa merkitä murtolukumuodossa, mikä helpottaa osamäärän tulkintaan.
Esimerkki 4.
(2x : 3y)3 = (2x)3 : (3y)3 = 8x3 : 27y3
-------------------------------------------------------------------------------------------------------------------------------------------
5) potenssin potenssi
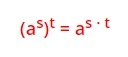
Potenssin korotus potenssiin tarkoittaa potenssien kertolaskua, mikäli potenssien välissä on sulkumerkintä. Mikäli sulkua ei ole, laskea potenssin potenssi normaalina potenssilaskuna.
Esimerkki 5.
(2x2)3 = 23x2 · 3 = 8x6
tai (2x2)3 = (2x2)(2x2)(2x2) = 2 · 2 · 2 · x2 · x2
-------------------------------------------------------------------------------------------------------------------------------------------
6) nolla eksponenttina
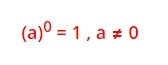
Luku potenssiin nolla on aina yksi, mikäli kantaluku on eri suuri kuin nolla. Tuloksen voi osoittaa useammallakin tavalla:
2 : 2 = 21 : 21 = 21 - 1 = 20 = 1 (yleensä todistus tehdään mille tahansa kantaluvulle a ≠ 0)
a · (1 : a) = a1 · a-1 = a1 + (-1) = a0 = 1 (luvun ja sen käänteisluvun tulo on aina 1)
-------------------------------------------------------------------------------------------------------------------------------------------
7) negatiivinen eksponentti
Negatiivinen eksponentti muutetaan positiivikseksi ja samalla kantaluku vaihdetaan käänteisluvuksi. Kantaluku kannattaa esittää murtolukuna ja sulkeiden sisällä.
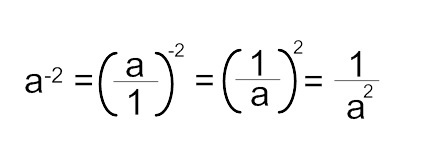
2.3 Eksponentin ratkaiseminen
Eksponentti laskuissa tuntematon muuttuja x voi esiintyä myös eksponenttina. Tarkastellaan tätä esimerkkien kautta.
Esimerkki 1.
Esimerkki 2.
→ Kirjoitetaan lauseke uudestaan muodossa 2x+1 = 24
→ x + 1 = 4
→ x = 3
Esimerkki 3.
23,2 = 9,1895...
23,3 = 9,8491...
23,4 = 10,5560...
23,35 = 10,1961...
23,32 = 9,9866...
Jatkamalla kokeilua pääsemme tulokseen x ≈ 3,322.
Tällaiset tehtävät, missä tuntematon muuttuja on eksponenttina, on paljon helpompi ratkaista logaritmilaskennan avulla.
Esimerkki 1.
2x = 8
Tiedetään, että 23 = 8, joten vastaukseksi saadaan x = 3. Lasku oli helppo suorittaa, kun eksponenttina on kokonaisluku.Esimerkki 2.
2x+1 = 16
→ Kirjoitetaan lauseke uudestaan muodossa 2x+1 = 24
→ x + 1 = 4
→ x = 3
Esimerkki 3.
2x = 10
Tiedetään, että 23 = 8 ja että 24 = 16. Nyt muuttujan x arvo on siis luku arvojen 3 ja 4 väliltä - desimaaliluku. Haetaan vastaus kokeilemalla.23,2 = 9,1895...
23,3 = 9,8491...
23,4 = 10,5560...
23,35 = 10,1961...
23,32 = 9,9866...
Jatkamalla kokeilua pääsemme tulokseen x ≈ 3,322.
Tällaiset tehtävät, missä tuntematon muuttuja on eksponenttina, on paljon helpompi ratkaista logaritmilaskennan avulla.
2.4. Logaritmi
Logaritmilaskenta on matemaattinen menetelmä laskea eksponenttilaskentaa käänteisesti. Logaritmien avulla pystytään ratkaisemaan siis eksponenttien arvoja.
Vastaavasti voidaan ajatella, että neliöjuuri on potenssin kaksi käänteinen laskutoimitus.
 Esimerkkejä.
Esimerkkejä.
a) 32 = 9 → log39 = 2
b) 34 = 81 → log381 = 4
c) 103 = 1000 → log101000 = 3
--------------------------------------------------------------------------------------------------------
Laskimessa käytetään vain 10-kantaisen logaritmin (LOG) ja luonnollisen logaritmin (LN) laskentaperusteita.
lg = 10-kantainen logaritmi
ln = e-kantainen logaritmi
--------------------------------------------------------------------------------------------------------
Siksi on hyödyllistä käyttää laskuissa kantaluvun vaihtosääntöä, jos kantalukuna on jokin muu luku kuin 10 tai e.
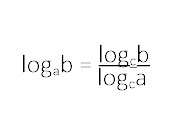
Esimerkki.
Ratkaistaan yhtälö 4x = 50.
Logaritmin avulla saadaan x = log450. Tätä ei voi kuitenkaan suoraan laskimella laskea, koska kantaluvulle neljä ei ole määritelty laskimen toimintoja. Käytetään kantaluvun vaihtosääntöä ja vaihdetaan kantaluvuksi 10, koska silloin voidaan käyttää laskinta apuna.
x = log450 = log1050 : log104 = lg50 : lg4 = 2,8219... ≈ 2,82
Vastaavasti voidaan ajatella, että neliöjuuri on potenssin kaksi käänteinen laskutoimitus.
 Esimerkkejä.
Esimerkkejä.a) 32 = 9 → log39 = 2
b) 34 = 81 → log381 = 4
c) 103 = 1000 → log101000 = 3
--------------------------------------------------------------------------------------------------------
Laskimessa käytetään vain 10-kantaisen logaritmin (LOG) ja luonnollisen logaritmin (LN) laskentaperusteita.
lg = 10-kantainen logaritmi
ln = e-kantainen logaritmi
--------------------------------------------------------------------------------------------------------
Siksi on hyödyllistä käyttää laskuissa kantaluvun vaihtosääntöä, jos kantalukuna on jokin muu luku kuin 10 tai e.
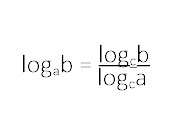
Esimerkki.
Ratkaistaan yhtälö 4x = 50.
Logaritmin avulla saadaan x = log450. Tätä ei voi kuitenkaan suoraan laskimella laskea, koska kantaluvulle neljä ei ole määritelty laskimen toimintoja. Käytetään kantaluvun vaihtosääntöä ja vaihdetaan kantaluvuksi 10, koska silloin voidaan käyttää laskinta apuna.
x = log450 = log1050 : log104 = lg50 : lg4 = 2,8219... ≈ 2,82
2.5. Logaritmin laskusäännöt
ekstraosio!
Tutustu videoiden kautta logaritmien laskusääntöihin ja tee niihin liittyvät lisätehtävät.
https://opetus.tv/maa/maa8/logaritmi/
Tutustu videoiden kautta logaritmien laskusääntöihin ja tee niihin liittyvät lisätehtävät.
https://opetus.tv/maa/maa8/logaritmi/