3. Funktio
3.1 Funktio
Esimerkki 1.
Bensiini maksaan 1,50 € litralta. Taulukoidaan ostetun bensiinin hinta taulukoksi.
1 litra → 1 · 1,50 € = 1,50 €
2 litraa → 2 · 1,50 € = 3,00 €
3 litraa → 3 · 1,50 € = 4,50 €
· ·
· ·
· ·
10 litraa → 10 · 1,50 € = 15 €
Maksettava hinta saadaan siis kertomalla ostettujen bensalitrojen määrä bensiinin yksikköhinnalla. Matemaattisesti tämä voidaan esittää muodossa h(x) = x · 1,50 = 1,50x.
---------------------------------------------------------------------------------------------------------------------------------------------
Funktiomerkinnässä tulee aina olla funktion nimi, muuttuja sekä funktiolauseke.
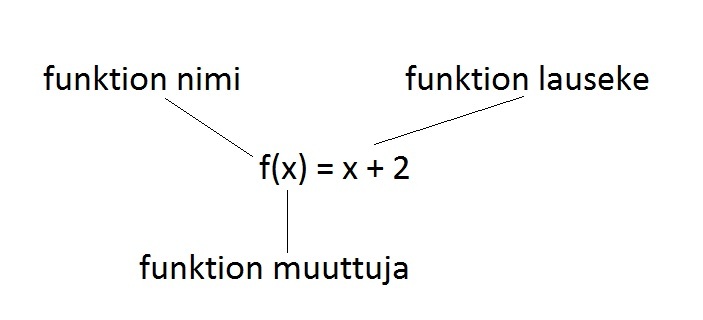
Esimerkki 2.
Esimerkissä 1 funktio esitettiin muodossa h(x) = 1,50x.
→ funktion nimi on h
→ funktion muuttujakirjain on x
→ funktion lauseke on 1,50 · x eli 1,50x
---------------------------------------------------------------------------------------------------------------------------------------------
Sijoittamalla funktion muuttujakirjaimen paikalle numero, voidaan laskea funktiolle arvo. Funktion arvo tarkoittaa siis funktion lausekkeen tuottamaa tulosta, joka saadaan tuntemalla muuttujakirjaimen arvo. Huomaa, että funktiot on määritelty usein monelle eri muuttujan arvolle, joten yksittäinen funktio voi saada useita eri arvoja.
Vastaavasti muuttujan arvo voidaan laskea, mikäli tiedetään funktion lauseke ja funktion arvo. Merkitsemällä lauseke yhtäsuureksi funktion arvon kanssa saadaan yhtälö, josta muuttujan arvo voidaan laskea.
Esimerkki 3.
a) käyttämällä esimerkin 1 laskukaavaa, laske hinta 68 litralle bensiiniä.
→ funktio hinnalle on h(x) = 1,50x
→ sijoitetaan muuttujan paikalle arvo 68.
→ h(68) = 1,50 · 68 = 102
→ vastaus: 68 litraa bensiiniä maksaa 102 euroa.
b) kuinka paljon bensiiniä saa ostettua, jos bensiiniä ostetaan 135 eurolla?
→ tiedetään funktion arvo 135 €, mutta muuttujan arvo on tuntematon x.
→ h(x) = 1,50 · x = 135
→ x = 135 : 1,50 = 90
→ vastaus: 135 eurolla saa 90 litraa bensiiniä.
---------------------------------------------------------------------------------------------------------------------------------------------
Funktion määrittelyjoukolla tarkoitetaan niitä muuttujan arvoja, joilla funktion lauseke tuottaa funktion arvon. Funktion määrittelyjoukko tulee tarkistaa ennen funktion laskuja.
Muista, että jakaja ei saa olla koskaan arvoltaan nolla. Kannattaa siis tarkastaa, onko olemassa sellaisia muuttujan arvoja, jotka tuottavat jakajaksi nollan. Tällaiset muuttujat on poistettava määrittelyjoukosta.
Lähtökohtaisesti määrittelyjoukkona pidetään kaikkia lukuja eli reaalilukuja.
Esimerkki 4.
Määritellään funktio seuraavasti: funktion arvo saadaan jakamalla luku 100 muuttujan arvolla. Funktion nimi olkoot t ja muuttujakirjain s.
→ funktio on muotoa t(s) = 100 : s
→ Onko olemassa lukuja, jotka eivät sovi muuttujan s paikalle em. lausekkeessa?
→ 100 : 0 ei ole määritelty, joten luku 0 ei sovi muuttujaksi, kaikki muut luvut sopivat muuttujiksi.
→ funktion määrittelyjoukko on Mt = R \ 0
---------------------------------------------------------------------------------------------------------------------------------------------
Niitä muuttujia, joilla funktio saa arvon nolla, kutsutaan funktion nollakohdiksi. Näiden nollakohtien ratkaiseminen suoritetaan useimmin yhtälön avulla merkitsemällä funktion lauseke yhtäsuureksi kuin nolla. Toinen tapa selvittää nollakohta, on piirtää funktion kuvaaja ja tulkita nollakohta suoraan kuvaajasta. Yhtälön käyttäminen on kuitenkin laskennallisena menetelmänä tarkempi.
Nollakohtien selvittäminen auttaa tulkitsemaan kuvaajaa. Esimerkiksi funktion positiivisuus ja negatiivisuus tarkastetaan nollakohtien avulla.
Esimerkki 5.
a) määritä funktion k(u) = 5u - 18 nollakohdat
→ 5u - 18 = 0
→ 5u = 0 + 18
→ 5u = 18 |:5
→ u = 18 : 5
→ u = 3,6
→ vastaus: funktion nollakohta saadaan muuttujan arvolla 3,6
b) määritä funktion g(h) = h2 + 5h + 6 nollakohdat
→ h2 + 5h + 6 = 0
→ (h + 2)(h + 3) = 0
→ h = -2 tai h = -3
→ vastaus: funktion nollakohdat saadaan muuttujan arvoilla -2 ja -3.
---------------------------------------------------------------------------------------------------------------------------------------------
3.2 Funktion kuvaaja
Funktioita voidaan kuvata myös kuvaajan avulla. Funktion lausekkeen avulla voidaan laskea yksittäistä muuttujan (x) arvoa vastaava funktion arvo (y).
Kuvaajan tulkinta on epätarkka laskentamenetelmä, mutta kuvaajien käyttäminen helpottaa usein tehtävän ratkaisua.
Kuvaajan avulla voidaan arvioida funktion arvoja, kun tiedetään muuttujien arvot. Sama pätee toiseen suuntaan eli funktion arvojen ja kuvaajan avulla voidaan arvioida muuttujien arvoja.
Esimerkki 1. Kuvaajan tulkinta.
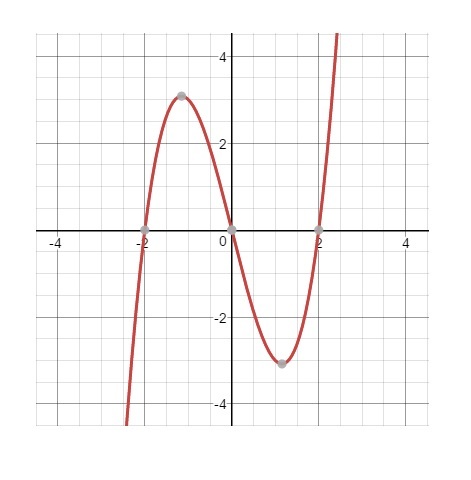a) Mikä on funktion arvo kohdassa 0?
b) Mikä on funktion arvo muuttujan arvolla x = 1,5?
c) Millä muuttujan arvolla funktio saa arvon nolla?
d) Millä muuttujan arvolla funktio saa arvon -3?
e) Millä muuttujien arvoilla funktio saa vain positiivisia arvoja?
-------------------------------------------------------------------------------------------------------------------------------------------
Funktion positiivisuus ja negatiivisuus tarkastellaan y-akseliin nähden. Vastaukset ilmoitetaan muuttujan eli x-akselin arvoilla. Ensimmäinen tehtävä on kuitenkin selvittää funktiot nollakohdat, koska niiden avulla saadaan ns. rajapisteet x-akselille.
Funktio on positiivinen, kun se kulkee x-akselin yläpuolella eli funktion arvot ovat suurempia kuin nolla.
Funktio on negatiivinen, kun se kulkee x-akselin alapuolella eli funktion arvot ovat pienempiä kuin nolla.
Esimerkki 2. Tutkitaan funktion f(x) = x3 - 4x kuvaajaa.
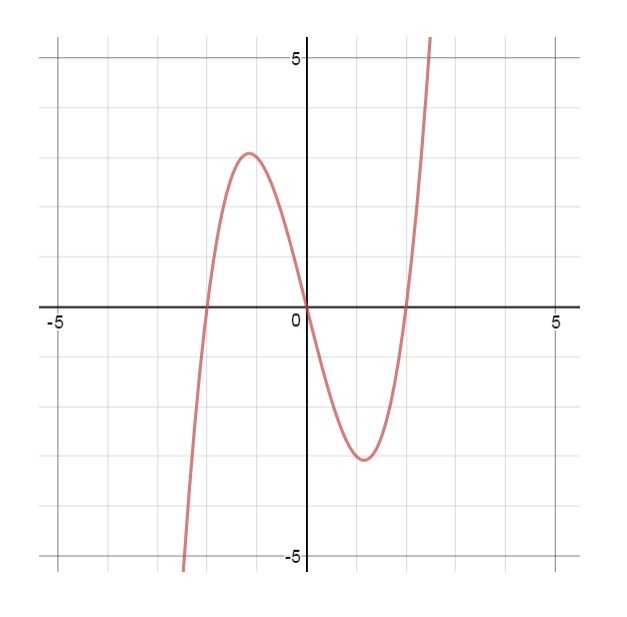
→ aloitetaan nollakohtien selvittämisellä. Kuvaajasta on helppo huomata, että nollakohdat saadaan muuttujan arvoilla x= -2, x = 0 ja x = 2. Näiden avulla ilmoitetaan seuraavat vastaukset.
→ funktio on x-akselin yläpuolella eli positiivinen silloin, x on lukujen -2 ja nolla välillä. Samoin funktio on positiivinen, kun muuttujan arvot ovat suurempia kuin 2.
→ f(x) > 0, kun -2 < x < 0 tai x > 2
→ funktio on x-akselin alapuolella eli negatiivinen silloin, x on lukujen 0 ja 2 välillä. Samoin funktio on negatiivinen, kun muuttujan arvot ovat pienempiä kuin -2.
→ f(x) < 0, kun x < -2 tai 0 < x < 2
-------------------------------------------------------------------------------------------------------------------------------------------
Funkio voidaan piirtää ja mallintaa joko laskemalla apupisteet ja merkitsemällä ne koordinaatistoon tai käyttämällä sopivaa sähköistä apuvälinettä, kuten graafiset laskimet, tablettisovellukset tai valmiit selainsovellukset. Kurssin aikana harjoitellaan molempia tekniikoita.
Funktion jokaista muuttujaa vastaa jokin tietty (yksi) funktion arvo. Muuttujat merkitään x-akselin pisteiksi ja vastaavat funktion arvot y-akselin pisteiksi. Siten jokaisesta funktiosta voidaan laskea pistepareja (x,y), jotka voidaan sijoittaa koordinaatistoon. Laskemalla riittävän monta pistettä, saadaan aikaan funktion kuvaaja.
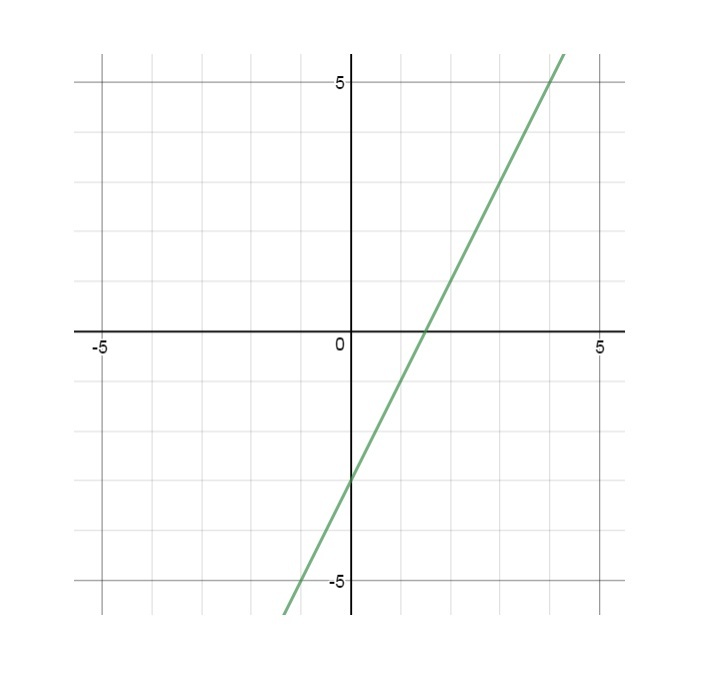
Esimerkki 3.
Piirretään funktion f(x) = 2x - 3 kuvaaja
Funktio voidaan kirjoittaa muodossa y = 2x - 3
Taulukoidaan funktiolle muuttujat (x) ja niitä vastaavat arvot (y)
| muuttujan arvo x | funktion arvo y | koordinaatiston pistepari |
|
x = 0 |
y = 2 · 0 - 3 = -3 |
(0,-3) |
|
x = 1 |
y = 2 · 1 - 3 = -1 |
(1,-1) |
|
x = 2 |
y = 2 · 2 - 3 = 1 |
(2,1) |
Sijoittamalla pisteet koordinaatistoon huomataan, että kuvaaja on suora. Tämän olisi voinut huomata heti funktion lausekkeesta, joka on ensimmäistä astetta (eli suoran yhtälö).
-------------------------------------------------------------------------------------------------------------------------------------------