2.4. Logaritmi
Logaritmilaskenta on matemaattinen menetelmä laskea eksponenttilaskentaa käänteisesti. Logaritmien avulla pystytään ratkaisemaan siis eksponenttien arvoja.
Vastaavasti voidaan ajatella, että neliöjuuri on potenssin kaksi käänteinen laskutoimitus.
 Esimerkkejä.
Esimerkkejä.
a) 32 = 9 → log39 = 2
b) 34 = 81 → log381 = 4
c) 103 = 1000 → log101000 = 3
--------------------------------------------------------------------------------------------------------
Laskimessa käytetään vain 10-kantaisen logaritmin (LOG) ja luonnollisen logaritmin (LN) laskentaperusteita.
lg = 10-kantainen logaritmi
ln = e-kantainen logaritmi
--------------------------------------------------------------------------------------------------------
Siksi on hyödyllistä käyttää laskuissa kantaluvun vaihtosääntöä, jos kantalukuna on jokin muu luku kuin 10 tai e.
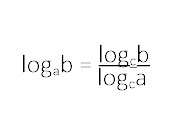
Esimerkki.
Ratkaistaan yhtälö 4x = 50.
Logaritmin avulla saadaan x = log450. Tätä ei voi kuitenkaan suoraan laskimella laskea, koska kantaluvulle neljä ei ole määritelty laskimen toimintoja. Käytetään kantaluvun vaihtosääntöä ja vaihdetaan kantaluvuksi 10, koska silloin voidaan käyttää laskinta apuna.
x = log450 = log1050 : log104 = lg50 : lg4 = 2,8219... ≈ 2,82
Vastaavasti voidaan ajatella, että neliöjuuri on potenssin kaksi käänteinen laskutoimitus.
 Esimerkkejä.
Esimerkkejä.a) 32 = 9 → log39 = 2
b) 34 = 81 → log381 = 4
c) 103 = 1000 → log101000 = 3
--------------------------------------------------------------------------------------------------------
Laskimessa käytetään vain 10-kantaisen logaritmin (LOG) ja luonnollisen logaritmin (LN) laskentaperusteita.
lg = 10-kantainen logaritmi
ln = e-kantainen logaritmi
--------------------------------------------------------------------------------------------------------
Siksi on hyödyllistä käyttää laskuissa kantaluvun vaihtosääntöä, jos kantalukuna on jokin muu luku kuin 10 tai e.
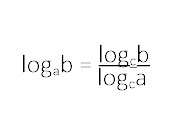
Esimerkki.
Ratkaistaan yhtälö 4x = 50.
Logaritmin avulla saadaan x = log450. Tätä ei voi kuitenkaan suoraan laskimella laskea, koska kantaluvulle neljä ei ole määritelty laskimen toimintoja. Käytetään kantaluvun vaihtosääntöä ja vaihdetaan kantaluvuksi 10, koska silloin voidaan käyttää laskinta apuna.
x = log450 = log1050 : log104 = lg50 : lg4 = 2,8219... ≈ 2,82