Ohjelmointi 7. luokan matematiikassa
Ohjelmointi 7. luokan matematiikassa.
Nämä esimerkit on tehty Processing-ohjelmointikielellä. Näitä esimerkkejä saa vapaasti käyttää omassa opetuksessa.
Peruslaskutoimitukset
Ohjelma, joka havainnollistaa yhteen-, vähennys-, kerto- ja jakolaskua.
Tällöin ohjelma tulostaa seuraavaa.

Huomio: Jakolaskuissa ainakin yhden luvun on oltava desimaaliluku tai muuten luku katkaistaan kokonaisluvuksi. Desimaaliluku kirjoitetaan pisteen avulla.
void setup () {
size(400,200); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
}
void draw () {
text(3+5,10,20);
text(3-5,10,40);
text(3*5,10,60);
text(3.0/5.0,10,80);
}
Tällöin ohjelma tulostaa seuraavaa.

Huomio: Jakolaskuissa ainakin yhden luvun on oltava desimaaliluku tai muuten luku katkaistaan kokonaisluvuksi. Desimaaliluku kirjoitetaan pisteen avulla.
Lukusuora
Kun haluamme sijoittaa pisteitä x-akselille, niin silloin x-akselin piirtämisestä ja pisteiden sijoittamisesta kannattaa tehdä oma aliohjelmansa. Tällöin tarvitsemme kirjoittaa vain komennot: xakseli(); ja x(luku); void draw ()-lohkoon. Kokonainen ohjelma on seuraava.
Tällöin ohjelma tulostaa
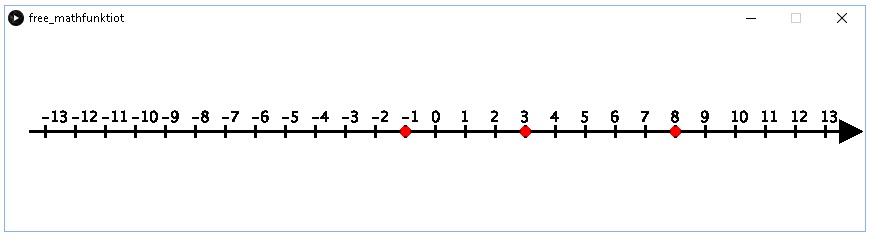
Kun kirjoitat laskutoimituksen komenon: x(luku) sisälle, niin voit havainnollistaa laskutoimituksia lukusuoralla.
void setup () {
size(860,200); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(15); // Tekstin koko 15
}
void draw () {
xakseli();
x(3);
x(3-4); // 3-4 = -1
x(3+5); // 3+5 = 8
}
void xakseli() {
translate(430,100); // Origo ikkunan keskelle
strokeWeight(2); // Viivan paksuus 2
stroke(0); // Viivan väri musta
line(-405,0,405,0); // x-askeli
for(int a=-13; a<=13; a++) {
line(30*a,-5,30*a,5); // asteikko
text(a,30*a-5,-10); // Lukuarvot [-13,13]
}
triangle(405,10,405,-10,425,0); // Kolmio
}
void x(float a) {
float x = map(a,-10,10,-300,300);
stroke(255,0,0); // Punainen
strokeWeight(10); // Pisteen koko 10
point(x,0); // Piirrä piste
}
Tällöin ohjelma tulostaa

Kun kirjoitat laskutoimituksen komenon: x(luku) sisälle, niin voit havainnollistaa laskutoimituksia lukusuoralla.
Laskujärjestys
Haluamme laskea seuraavat laskutoimitukset:
[[$ 16-\frac{12}{6}-4 $]]
[[$ \frac{16-12}{6-4} $]]
[[$ \frac{\left(12+3\right)\cdot\left(7-5\right)}{48:\left(5+3\right)} $]]
[[$ \left(14-6\right)-\left(\left(30-\left(11+9\right)\right)-5\right) $]]
Ohjelma, joka havainnollistaa laskujärjestystä on seuraavanlainen.
Tällöin ohjelma tulostaa seuraavaa.

Huomio: Näissä laskuissa oli jo tiedossa, että vastaus on kokonaisluku, niin tässä ei ole käytetty laskutoimituksissa desimaalilukuja.
[[$ 16-\frac{12}{6}-4 $]]
[[$ \frac{16-12}{6-4} $]]
[[$ \frac{\left(12+3\right)\cdot\left(7-5\right)}{48:\left(5+3\right)} $]]
[[$ \left(14-6\right)-\left(\left(30-\left(11+9\right)\right)-5\right) $]]
Ohjelma, joka havainnollistaa laskujärjestystä on seuraavanlainen.
void setup () {
size(400,200); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
}
void draw () {
text(16-12/6-4,10,20);
text((16-12)/(6-4),10,40);
text((12+3)*(7-5)/(48/(5+3)),10,60);
text((14-6)-((30-(11+9))-5),10,80);
}
Tällöin ohjelma tulostaa seuraavaa.

Huomio: Näissä laskuissa oli jo tiedossa, että vastaus on kokonaisluku, niin tässä ei ole käytetty laskutoimituksissa desimaalilukuja.
Luvun pyöristäminen
Ohjelma, joka havainnollistaa lukujen pyöristämistä. Komento nfc(luku,desimaalia) pyöristää luvun annetun desimaalin tarkkuudella. Komento round(luku) antaa vastauksena kokonaisluvun.
Tällöin ohjelma tulostaa seuraavaa.

void setup () {
size(400,200); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
}
void draw () {
text(0.609,10,20); // Alkuperäinen luku
text(nfc(0.609,1),10,40); // 1-desimaali
text(nfc(0.609,2),10,60); // 2-desimaalia
text(round(0.609),10,80); // Kokonaisluku
}
Tällöin ohjelma tulostaa seuraavaa.

Murtolukujen yhteenlasku
Ohjelma, joka havainnolistaa murtolukujen yhteenlaskua
Tällöin ohjelma tulostaa seuraavaa.

Ohjelmassa on se puute, että jos me haluamme tulostaa jonkin toisen murtolukujen yhteenlaskun, niin joudumme paljon muuttamaan koodia. On parempi käyttää muuttujia. Luvun 2 tilalle laitamme muuttujan a, luvun 7 tilalle laitamme muuttujan b, luvun 1 tilalle laitamme muuttujan c ja luvun 3 tilalle laitamme muuttujan d. Eli kahden murtoluvun yhteenlasku voidaan laskea kaavalla.
[[$ \frac{a}{b}+\frac{c}{d}=\frac{ad}{bd}+\frac{bc}{bd}=\frac{ad+bc}{bd} $]]
Sama ohjelma, muuttujien avulla kirjoitettuna on seuraava.
Kokeile muuttaa muuttujien a,b,c ja d tilalle jokin muu luku. Kuinka muuttaisit koodia, jos haluat laskea murtolukujen vähennys, kerto tai jakolaskun.
void setup () {
size(400,200); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
strokeWeight(3); // Viivan paksuus 3
}
void draw () {
text(2,10,20);
line(10,28,20,28);
text(7,10,50);
text("+",23,33);
text(1,40,20);
line(40,28,50,28);
text(3,40,50);
text("=",57,33);
text(2*3,80,20);
line(80,28,100,28);
text(7*3,80,50);
text("+",102,33);
text(1*7,120,20);
line(120,28,140,28);
text(7*3,120,50);
text("=",142,33);
text(2*3+1*7,160,20);
line(160,28,180,28);
text(7*3,160,50);
}
Tällöin ohjelma tulostaa seuraavaa.

Ohjelmassa on se puute, että jos me haluamme tulostaa jonkin toisen murtolukujen yhteenlaskun, niin joudumme paljon muuttamaan koodia. On parempi käyttää muuttujia. Luvun 2 tilalle laitamme muuttujan a, luvun 7 tilalle laitamme muuttujan b, luvun 1 tilalle laitamme muuttujan c ja luvun 3 tilalle laitamme muuttujan d. Eli kahden murtoluvun yhteenlasku voidaan laskea kaavalla.
[[$ \frac{a}{b}+\frac{c}{d}=\frac{ad}{bd}+\frac{bc}{bd}=\frac{ad+bc}{bd} $]]
Sama ohjelma, muuttujien avulla kirjoitettuna on seuraava.
void setup () {
size(400,200); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
strokeWeight(3); // Viivan paksuus 3
}
void draw () {
int a = 2;
int b = 7;
int c = 1;
int d = 3;
text(a,10,20);
line(10,28,20,28);
text(b,10,50);
text("+",23,33);
text(c,40,20);
line(40,28,50,28);
text(d,40,50);
text("=",57,33);
text(a*d,80,20);
line(80,28,100,28);
text(b*d,80,50);
text("+",102,33);
text(c*b,120,20);
line(120,28,140,28);
text(b*d,120,50);
text("=",142,33);
text(a*d+c*b,160,20);
line(160,28,180,28);
text(b*d,160,50);
}
Kokeile muuttaa muuttujien a,b,c ja d tilalle jokin muu luku. Kuinka muuttaisit koodia, jos haluat laskea murtolukujen vähennys, kerto tai jakolaskun.
Esimerkki: Itseisarvo ja vastaluku
Ohjelma, joka havainnollistaa itseisarvon ja vastaluvun laskemista on seuraava.
Tällöin ohjelma tulostaa.

Huomio: Tekstin, joka on lainausmerkkien välissä ja laskutoimituksen välissä käytetään erottimena + merkkiä. Processing ohjelman oma komento: abs(luku) palauttaa luvun itseisarvon.
void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
}
void draw () {
text("|3| = "+abs(3),10,20); // Itseisarvo
text("|-4| = "+abs(-4),10,50); // Itseisarvo
text("-(+3) = "+(-(+3)),10,80); // Vastaluku
text("-(-4)) = "+(-(-4)),10,110); // Vastaluku
text("15+(-2)-(-7) = "+(15+(-2)-(-7)),10,140); // Sulkumerkkien poistaminen
text("28-(-10)-9+(-11) = "+(28-(-10)-9+(-11)),10,170); // Sulkumerkkien poistaminen
}
Tällöin ohjelma tulostaa.

Huomio: Tekstin, joka on lainausmerkkien välissä ja laskutoimituksen välissä käytetään erottimena + merkkiä. Processing ohjelman oma komento: abs(luku) palauttaa luvun itseisarvon.
Piste xy-koordinaatistossa
Haluamme piirtää pisteet (4,3), (-5,7), (-6,-3) ja (5,-8) matematiikan xy-koordinaatistoon. Kaikkein järkevintä on tehdä oma aliohjelma pisteestä ja matematiikan xy-koordinaatistosta, joilloin näitä voidaan kutsua void draw ()-lohkosta. Katsotaan tästä esimerkki.
Tällöin ohjelma tuostaa

void setup () {
size(600,600); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
}
void draw () {
koordinaatisto();
piste(4,3);
piste(-5,7);
piste(-6,-3);
piste(5,-8);
}
void koordinaatisto () {
translate(300,300); // Origo ikkunan keskelle
scale(1,-1); // Peilaa y-koordinaatit
strokeWeight(1); // Viivan paksuus 1
stroke(200); // Viivan väri harmaa
for(int a=-10; a<=10; a++) { // Piirrä ruudukko
line(30*a,-300,30*a,300);
line(-300,30*a,300,30*a);
}
strokeWeight(2); // Viivan paksuus 2
stroke(0); // Viivan väri musta
line(-300,0,300,0); // x-askeli
line(0,-300,0,300); // y-akseli
}
void piste(float x, float y) {
float x2 = map(x,-10,10,-300,300); // Skaalaa asteikolta [-10,10] asteikolle [-300,300]
float y2 = map(y,-10,10,-300,300); // Skaalaa asteikolta [-10,10] asteikolle [-300,300]
strokeWeight(10); // Viivan paksuus 10
point(x2,y2); // Piirrä piste
}
Tällöin ohjelma tuostaa

Esimerkki: Janan piirtäminen
Piirretään jana pisteiden (-2,1) ja (4,5) välille, sekä pisteiden (-2,1) ja (3,-6) välille. Myös tässä esimerkikssä kannattaa tehdä oma aliohjelma, joka piirtää janan edellisessä esimerkikssä määriteltyyn matematiikan xy-koordinaatistoon. Mitä useammin kutsut jana()-kometoa void draw ()-lohkossa sitä useampi jana piirretään.
Kun ajat ohjelman, niin se tulostaa seuraavaa.

Kuvasta voisi selvittää esimerkiksi sen, että onko janojen välinen kulma terävä vai tylppä.
void setup () {
size(600,600); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
}
void draw () {
koordinaatisto();
jana(-2,1,4,5);
jana(-2,1,3,-6);
}
void koordinaatisto () {
translate(300,300); // Origo ikkunan keskelle
scale(1,-1); // Peilaa y-koordinaatit
strokeWeight(1); // Viivan paksuus 1
stroke(200); // Viivan väri harmaa
for(int a=-10; a<=10; a++) { // Piirrä ruudukko
line(30*a,-300,30*a,300);
line(-300,30*a,300,30*a);
}
strokeWeight(2); // Viivan paksuus 2
stroke(0); // Viivan väri musta
line(-300,0,300,0); // x-askeli
line(0,-300,0,300); // y-akseli
}
void jana(float a, float b, float c, float d) {
float x1 = map(a,-10,10,-300,300); // Skaalaa asteikolta [-10,10] asteikolle [-300,300]
float y1 = map(b,-10,10,-300,300); // Skaalaa asteikolta [-10,10] asteikolle [-300,300]
float x2 = map(c,-10,10,-300,300); // Skaalaa asteikolta [-10,10] asteikolle [-300,300]
float y2 = map(d,-10,10,-300,300); // Skaalaa asteikolta [-10,10] asteikolle [-300,300]
strokeWeight(10); // Viivan paksuus 10
point(x1,y1); // Piirrä piste
point(x2,y2); // Piirrä piste
strokeWeight(3); // Viivan paksuus 3
line(x1,y1,x2,y2); // Piirrä viiva
}
Kun ajat ohjelman, niin se tulostaa seuraavaa.

Kuvasta voisi selvittää esimerkiksi sen, että onko janojen välinen kulma terävä vai tylppä.
Ympyrä xy-koordinaatistossa
Haluamme piirtää ympyrän, jonka säde on 4 pisteeseen (4,5) ja ympyrän, jonka säde on 2 pisteeseen (-3,-6). Ohjelma, joka piirtää ympyrän xy-koordinaatistoon on seuraavanlainen.
Tällöin ohjelma tulostaa seuraavaa.

void setup () {
size(600,600); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
}
void draw () {
koordinaatisto();
ympyra(4,5,4);
ympyra(-3,-6,2);
}
void koordinaatisto () {
translate(300,300); // Origo ikkunan keskelle
scale(1,-1); // Peilaa y-koordinaatit
strokeWeight(1); // Viivan paksuus 1
stroke(200); // Viivan väri harmaa
for(int a=-10; a<=10; a++) { // Piirrä ruudukko
line(30*a,-300,30*a,300);
line(-300,30*a,300,30*a);
}
strokeWeight(2); // Viivan paksuus 2
stroke(0); // Viivan väri musta
line(-300,0,300,0); // x-askeli
line(0,-300,0,300); // y-akseli
}
void ympyra(float a, float b, float c) {
float x = map(a,-10,10,-300,300); // Skaalaa asteikolta [-10,10] asteikolle [-300,300]
float y = map(b,-10,10,-300,300); // Skaalaa asteikolta [-10,10] asteikolle [-300,300]
float r = map(c,-10,10,-300,300); // Skaalaa asteikolta [-10,10] asteikolle [-300,300]
noFill(); // Poista täyttö
strokeWeight(3); // Viivan paksuus 3
point(x,y); // Keskipiste
ellipse(x,y,2*r,2*r); // kehä
}
Tällöin ohjelma tulostaa seuraavaa.

Ympyrä
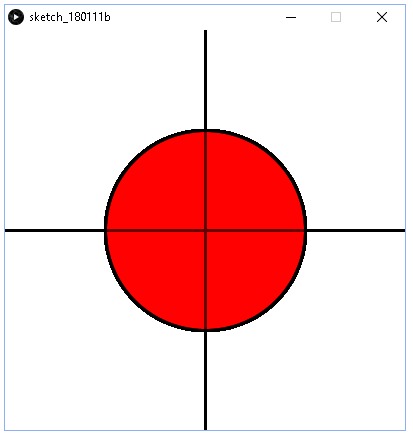
Piirretään ympyrä Processing-ohjelman omalla komennolla. Asetetaan ensin origo ikkunan keskelle ja peilataan y-koordinaatit, jolloin saamme aikaiseksi matematiikan xy-koordinaatiston. Ympyrän keskipiste on nyt origossa eli ikkunan keskellä ja ympyrän säde on 100 eli halkaisija on 200. Ohjelma ympyrän piirtämiseksi on seuraava.
Tällöin tulostuu.
void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
strokeWeight(3); // Reunaviivan paksuus 3
}
void draw () {
translate(200,200); // Origo ikkunan keskelle
scale(1,-1); // Peilaa y-koordinaatit
line(-200,0,200,0); // x-akseli
line(0,-200,0,200); // y-akseli
fill(255,0,0,100); // Punainen, läpinäkyvyys 100
ellipse(0,0,200,200); // Ympyrä, keskipiste (0,0), Halkaisija 200
}
Tällöin tulostuu.

Sektori
- Tehdään ohjelma, joka piirtää sektorin. Origo on ikkunan keskellä ja kiertosuunta on vastapäivään. Sektorin keskipiste on (0,0), halkaisija 200, aloituskulma kohdassa 45° myötäpäivään ja lopetuskulma kohdassa 135° myötäpäivään.
void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
strokeWeight(3); // Reunaviivan paksuus 3
}
void draw () {
translate(200,200); // Origo ikkunan keskelle
scale(1,-1); // Peilaa y-koordinaatit
fill(255,0,0); // Punainen
arc(0,0,200,200,radians(45), radians(135),PIE);
}
Tällöin tulostuu seuraavaa.

Huomio: Komento scale(1,-1); muuttaa kiertosuunnan vastapäivään.
Segmentti
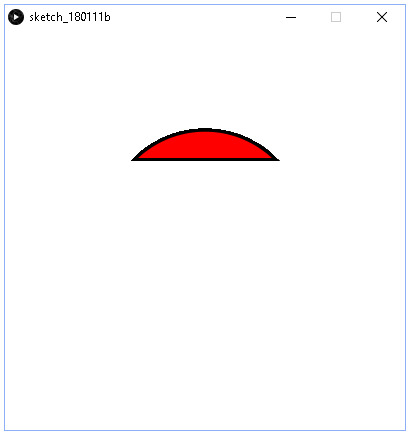
Tehdään ohjelma, joka piirtää segmentin. Origo on ikkunan keskellä ja kiertosuunta on vastapäivään. Segmentin keskipiste on (0,0), halkaisja 200, aloituskulma kohdassa 45° myötäpäivään ja lopetuskulma kohdassa 135° myötäpäivään. Nollakulma on idässä.
Tällöin tulostuu seuraavaa.
void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
strokeWeight(3); // Reunaviivan paksuus 3
}
void draw () {
translate(200,200); // Origo ikkunan keskelle
scale(1,-1); // Peilaa y-koordinaatit
fill(255,0,0); // Punainen
arc(0,0,200,200,radians(45), radians(135),CHORD);
}
Tällöin tulostuu seuraavaa.

Kaari
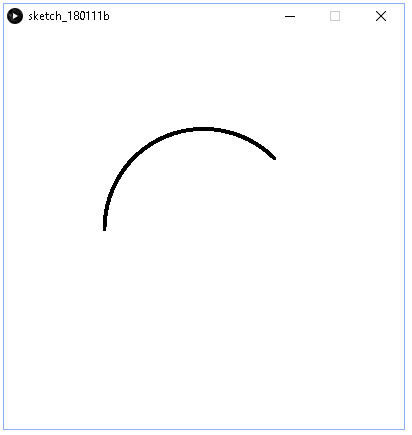
Tehdään ohjelma, joka piirtää kaaren. Origo on ikkunan keskellä ja kiertosuunta on vastapäivään. Kaaren keskipiste on (0,0), halkaisija 200, aloituskulma kohdassa 45° myötäpäivään ja lopetuskulma kohdassa 180° myötäpäivään. Nollakulma on idässä.
Tällöin tulostuu seuraavaa.
void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
strokeWeight(3); // Reunaviivan paksuus 3
}
void draw () {
translate(200,200); // Origo ikkunan keskelle
scale(1,-1); // Peilaa y-koordinaatit
noFill(); // Ei täyttöä
arc(0,0,200,200,radians(45), radians(180));
}
Tällöin tulostuu seuraavaa.

Kulmien luokittelu
Ohjelma, joka piirtää kulmia on seuraavanlainen.
Tällöin ohjelma tulostaa seuraavaa.
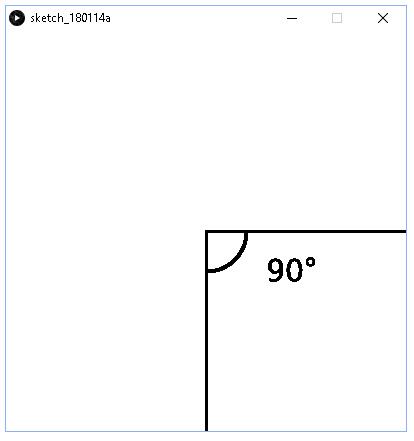
Ohjelmalla voidaan havainnollistaa kaikki kulmat väliltä 0...360. Ohjelman avulla voidaan kulmia luokitella: nollakulma, terävä kulma, suora kulma, tylppä kulma, oikokulma, kupera kulma, täysi kulma.
void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
strokeWeight(3); // Reunaviivan paksuus 3
textSize(30); // Tekstin koko
}
void draw () {
int kulma = 90; // Voit muuttaa kulman 0 <= kulma <= 360
translate(200,200); // Origo ikkunan keskelle
noFill(); // Ei täyttöä
if (kulma == 0) {
line(0,0,200,0);
} else {
arc(0,0,800,800,radians(0),radians(kulma),PIE);
arc(0,0,80,80,radians(0),radians(kulma),PIE);
}
fill(0); // Musta tekstin väri
text(kulma+"°",60,50); // Tulosta kulma
}
Tällöin ohjelma tulostaa seuraavaa.

Ohjelmalla voidaan havainnollistaa kaikki kulmat väliltä 0...360. Ohjelman avulla voidaan kulmia luokitella: nollakulma, terävä kulma, suora kulma, tylppä kulma, oikokulma, kupera kulma, täysi kulma.
Vieruskulma
Tehdään ohjelma, joka havainnolistaa vieruskulmia. Laitetaan kulma muuttujaksi, niin kulman voi muuttaa mieleiseksi. Ohjelma on seuraavanlainen.
Tällöin ohjelma tulostaa.

void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
strokeWeight(3); // Reunaviivan paksuus 3
textSize(30); // Tekstin koko
}
void draw () {
int kulma = 50; // Voit muuttaa kulman
translate(200,200); // Origo ikkunan keskelle
line(-200,0,200,0); // Vaakaviiva
noFill(); // Ei täyttöä
arc(0,0,800,800,radians(0),radians(kulma),PIE);
arc(0,0,80,80,radians(0),radians(kulma),PIE);
fill(0); // Musta tekstin väri
text(kulma+"°",60,50); // Tulosta kulma
}
Tällöin ohjelma tulostaa.

Ristikulma
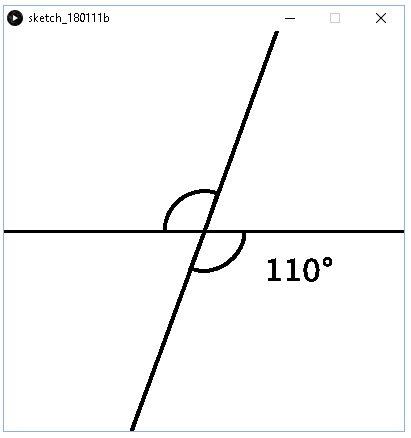
Tehdään ohjelma, joka havainnolistaa ristikulmia. Laitetaan kulma muuttujaksi, niin kulman voi muuttaa mieleiseksi. Ohjelma on seuraavanlainen.
Tällöin ohjelma tulostaa.
void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
strokeWeight(3); // Reunaviivan paksuus 3
textSize(30); // Tekstin koko
}
void draw () {
int kulma = 110; // Voit muuttaa kulman
translate(200,200); // Origo ikkunan keskelle
line(-200,0,200,0); // Vaakaviiva
noFill(); // Ei täyttöä
arc(0,0,800,800,radians(0),radians(kulma),PIE);
arc(0,0,80,80,radians(0),radians(kulma),PIE);
arc(0,0,800,800,radians(180),radians(kulma+180),PIE);
arc(0,0,80,80,radians(180),radians(kulma+180),PIE);
fill(0); // Musta tekstin väri
text(kulma+"°",60,50); // Tulosta kulma
}
Tällöin ohjelma tulostaa.

Yhdensuuntaisuus ja kohtisuoruus
Ohjelma, joka havainnolistaa kahnden suoran yhdensuuntaisuutta ja kohtisuoruutta on seuraavanlainen.
Tällöin ohjelma tulostaa seuraavaa.

Muuta muuttujien kulma1 ja kulma2 arvoja. Jos arvot ovat samat, niin suorat ovat yhdensuuntaiset. Jos arvojen erotus on 90, niin suorat ovat kohtisuorassa toisiaan vastaan.
void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
strokeWeight(3); // Reunaviivan paksuus 3
textSize(30); // Tekstin koko
}
void draw () {
int kulma1 = 30; // Voit muuttaa kulman
int kulma2 = 120; // Voi muuttaa kulman
translate(200,200); // Origo ikkunan keskelle
pushMatrix();
rotate(radians(kulma1));
line(-300,-5,300,-5);
popMatrix();
pushMatrix();
rotate(radians(kulma2));
line(-300,5,300,5);
popMatrix();
}
Tällöin ohjelma tulostaa seuraavaa.

Muuta muuttujien kulma1 ja kulma2 arvoja. Jos arvot ovat samat, niin suorat ovat yhdensuuntaiset. Jos arvojen erotus on 90, niin suorat ovat kohtisuorassa toisiaan vastaan.
Samankohtaiset kulmat
Ohjelma, joka havainnollistaa samankohtaisia kulmia on seuraavanlainen.
Tällöin ohjelma tulostaa seuraavaa.

Kun kulmat ovat samat, niin suorat ovat yhdensuuntaiset.
void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
strokeWeight(3); // Reunaviivan paksuus 3
textSize(25); // Tekstin koko
}
void draw () {
int kulma1 = 120; // Voit muuttaa kulman
int kulma2 = 110; // Voit muuttaa kulman
translate(200,200); // Origo ikkunan keskelle
line(-200,0,200,0); // Vaakaviiva
noFill(); // Ei täyttöä
arc(50,0,800,800,radians(0),radians(kulma1),PIE);
arc(50,0,40,40,radians(0),radians(kulma1),PIE);
arc(50,0,800,800,radians(180),radians(kulma1+180),PIE);
arc(-50,0,800,800,radians(0),radians(kulma2),PIE);
arc(-50,0,40,40,radians(0),radians(kulma2),PIE);
arc(-50,0,800,800,radians(180),radians(kulma2+180),PIE);
fill(0); // Musta tekstin väri
text(kulma1+"°",60,40); // Tulosta kulma
text(kulma2+"°",-40,40); // Tulosta kulma
}
Tällöin ohjelma tulostaa seuraavaa.

Kun kulmat ovat samat, niin suorat ovat yhdensuuntaiset.
Monikulmio
Piirretään viisikulmio matematiikan xy-kordinaatistoon ja piirretään siihen yhdestä nurkasta lähtevät lävistäjät. Ohjelma on seuraava.
Tällöin ohjelma tulostaa seuraavaa.

void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0,0,255); // Sininen
strokeWeight(3); // Reunaviivan paksuus 3
}
void draw () {
translate(200,200); // Origo ikkunan keskelle
scale(1,-1); // Peilaa y-koordinaatit
beginShape(); // Aloita monikulmio
vertex(100,100);
vertex(150,-100);
vertex(0,-150);
vertex(-150,-100);
vertex(-100,50);
endShape(CLOSE); // Lopeta monikulmio
line(100,100,0,-150); // Lävistäjä
line(100,100,-150,-100); // Lävistäjä
}
Tällöin ohjelma tulostaa seuraavaa.

Tasakylkinen kolmio
Piirretään tasakylkinen kolmio matematiikan xy-koordinaatistoon. Kolmion kanta on 200 ja korkeus 200.
Tällöin ohjelma tulostaa seuraavaa.

void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0,255,0); // Vihreä
strokeWeight(3); // Reunaviivan paksuus 3
}
void draw () {
translate(200,200); // Origo ikkunan keskelle
scale(1,-1); // Peilaa y-koordinaatit
triangle(100,-100,-100,-100,0,100);
}
Tällöin ohjelma tulostaa seuraavaa.

Suorakulmion piiri ja pinta-ala
Tehdään ohjelma, joka piirtää suorakulmion ja laskee suorakulmion piirin ja pinta-alan.
Nyt ohjelma tulostaa seuraavaa.

Kokeile muuttaa muuttujien kanta ja korkeus arvoja.
void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0,255,0); // Vihreä
strokeWeight(3); // Reunaviivan paksuus 3
textSize(20); // Tekstin koko 20
}
void draw () {
int kanta = 200; // Voit muuttaa arvon
int korkeus = 100; // Voit muuttaa arvon
fill(0,255,0); // Vihreä
rect(50,100,kanta,korkeus);
fill(0); // Musta
text("Kanta a = "+kanta+" ja korkeus b = "+korkeus,10,20);
text("Piiri p = "+(2*kanta+2*korkeus),10,50);
text("Pinta-ala A = "+(kanta*korkeus),10,80);
}
Nyt ohjelma tulostaa seuraavaa.

Kokeile muuttaa muuttujien kanta ja korkeus arvoja.
Peilaus origon suhteen
Tehdään ohjelma, joka piirtää suorakulmaisen kolmion matematiikan xy-kordinaatistoon, jonka nurkkapisteet ovat (50,50), (100,50) ja (50,100). Peilataan tämä kolmio origon suhteen. Ohjelma on seuraava.
Ohjelma tulostaa nyt seuraavaa.
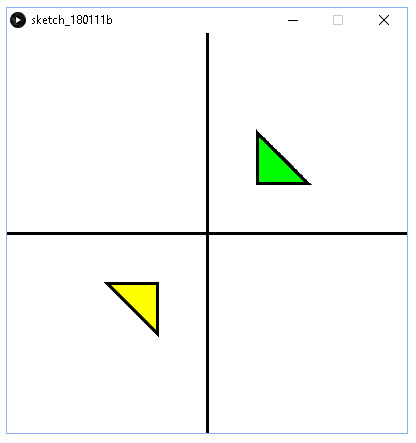
Jos haluat peilata vihreän kolmion x-askelin suhteen, niin kirjoita skaalaus-komento muotoon scale(-1,1). Jos haluat peilata vihreän kolmion y-akselin suhteen, niin kirjoita skaalaus-komento muotoon scale(1,-1).
void setup () {
size(400,400); // Ikkunan koko
background(255); // Taustaväri valkoinen
strokeWeight(3); // Reunaviivan paksuus 3
textSize(20);
}
void draw () {
translate(200,200);
scale(1,-1);
line(-200,0,200,0);
line(0,-200,0,200);
fill(0,255,0); // Vihreä
triangle(50,50,100,50,50,100);
fill(255,255,0); // keltainen
scale(-1,-1); // Peilauskomento
triangle(50,50,100,50,50,100);
}
Ohjelma tulostaa nyt seuraavaa.

Jos haluat peilata vihreän kolmion x-askelin suhteen, niin kirjoita skaalaus-komento muotoon scale(-1,1). Jos haluat peilata vihreän kolmion y-akselin suhteen, niin kirjoita skaalaus-komento muotoon scale(1,-1).
Potenssi
Tehdään ohjelma, joka laskee potensseja. Kun tulostamme lukuja potensiin, niin meidän on käytettävä unicode-merkkejä. Ohjelma on seuraavanlainen
Tällöin ohjelma tulostaa.

void setup () {
size(400,200); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
}
void draw () {
text("3\u00B2 = "+pow(3,2),10,30);
text("2\u00B3 = "+pow(2,3),10,60);
text("0,3\u2074 = "+pow(0.3,4),10,90);
text("0,3\u2074 = "+nfc(pow(0.3,4),4),10,120);
text("2\u207B\u2075 = "+pow(2,-5),10,150);
}
Tällöin ohjelma tulostaa.

Esimerkki: Funktion arvo
Tehdään ohjelma, joka laskee funktion arvon.
Tällöin ohjelma tulostaa.

Kokeile muuttaa muuttujalle x toinen arvo.
Huomaa, että kertomerkin voit tulostaa unicode merkillä: \u00B7
void setup () {
size(400,200); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
}
void draw () {
int x = -4;
int y = 2*x+5;
text("Olkoon f(x) = 2\u00B7x+5",10,20);
text("Muuttujan arvo x = "+x,10,50);
text("Funktion arvo f("+x+") = "+y,10,80);
}
Tällöin ohjelma tulostaa.

Kokeile muuttaa muuttujalle x toinen arvo.
Huomaa, että kertomerkin voit tulostaa unicode merkillä: \u00B7
Lukujono
Tehdään ohjelma, jonka avulla havainnollistetaan aritmeettista ja geometrista lukujonoa.
Tällöin ohjelma tulostaa.

int a = 2;
int b = 3;
int y = 1;
void setup () {
size(400,520); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
}
void draw () {
text(a,100,20*y);
text(b,200,20*y);
a = a+3; // aritmeettinen lukujono
b = b*2; // geometrinen lukujono
y++;
}
Tällöin ohjelma tulostaa.

Jaollisuuden tutkiminen
Tehdään ohjelma, joka tutkii millä luvulla tutkittava luku on jaollinen. Esimerkiksi jos haluamme selvittää millä luvulla luku 550 on jaollinen, niin se on seuraavanlainen.
Tällöin ohjelma tulostaa seuraavaa.

int x = 0; // Laskurin alkuarvo
void setup () {
size(400,520); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
}
void draw () {
int luku= 550; // vaihda tähän tutkittava luku 1 < x < 1 000 000 000
for (int a=1; a<=luku; a++) {
if (luku%a == 0) { // Onko jakojäännös nolla?
x++; // Laskuri kasvaa vain, jos löytyi jaollinen luku
text("Jaollinen luvulla: "+a,10,x*20);
}
if (a == luku) { x = 0; } // Kun kaikki luvut on tutkittu, niin nollaa laskuri
}
}
Tällöin ohjelma tulostaa seuraavaa.

Yhtälön ratkaisun etsiminen kokeilemalla
Kun etsimme yhtälön ratkaisua tietokoneella, niin silloin kannattaa laittaa laskuri tai for-silmukka, jonka avulla lasketaan yhtälön vasen ja yhtälön oikea puoli. Lisätään ohjelmaan ehto, että jos yhtälön oikea puoli on sama kuin yhtälön vasen puoli, niin muutetaan tekstin väriksi punainen, muutoin musta. Esimerkiksi yhtälön 2x-4 = x-1 ratkaisu löytyy seuraavalla ohjelmalla.
Kun ajamme ohjelman, niin näemme heti yhtälön ratkaisun eli kun x = 3, niin yhtälön vasen puoli = yhtälön oikea puoli.

int x =-11;
void setup () {
size(400,520); // Ikkunan koko
background(255); // Taustaväri valkoinen
fill(0); // Tekstin väri musta
textSize(20); // Tekstin koko 20
}
void draw () {
x++;
float y1 = 2*x-4;
float y2 = x-1;
if (y1 == y2) { fill(255,0,0); } else { fill(0); }
text("x = "+x,10,220+20*x);
text(y1,150,220+20*x);
text(y2,300,220+20*x);
}
Kun ajamme ohjelman, niin näemme heti yhtälön ratkaisun eli kun x = 3, niin yhtälön vasen puoli = yhtälön oikea puoli.
