1.4 Laskutoimituksia murtoluvuilla
Murtoluku
Rationaalilukujen yhteydessä määriteltiin rationaalilukujen joukkoon [[$\mathbb{Q}$]] kuuluviksi kaikki ne luvut, jotka voidaan esittää kahden kokonaisluvun suhteena, eli jakolaskuna [[$\frac{a}{b}$]], missä luvut [[$a,b \in \mathbb{Z}$]] ja [[$b\ne 0$]]. Tällaisten lukujen välisiä laskutoimituksia voidaan suorittaa ilman kyseisen jakolaskun laskemista.
Muodossa [[$\frac{a}{b}$]] esitettyä lukua kutsutaan luvun murtolukuesitykseksi.
Murtoluku tarkoittaa lukua, joka on esitetty murtolukumuodossa. Murtoluku [[$\frac{2}{3}$]] luetaan "kaksi kolmasosaa". Jakoviivan yläpuolista osaa kutsutaan osoittajaksi ja alapuolista osaa nimittäjäksi.
Osoittajasta nähdään, kuinka monta kappaletta kyseisiä osia on, ja nimittäjä ilmaisee yksittäisen osan koon. Esimerkiksi murtoluku [[$\frac{5}{6}$]] tarkoittaa viittä kappaletta kuudesosia, eli
[[$$\frac{5}{6}=5\cdot \frac{1}{6}=\left(\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\right)$$]]
Kokonaisluku voidaan esittää murtolukuna, jonka osoittajana on luku itse ja nimittäjänä luku yksi.
[[$$n=\frac{n}{1}$$]]
Luku yksi voidaan esittää murtolukuna, jolla on sama osoittaja ja nimittäjä.
[[$$1=\frac{n}{n}$$]]Sekaluku
Joskus ykköstä suuremmat murtoluvut esitetään sekalukuna. Sekaluvussa on kokonaisosa ja murto-osa. Murtolukujen laskutoimitusten yhteydessä on usein selvintä muuttaa kaikki sekaluvut ensin murtoluvuiksi ja sen jälkeen suorittaa laskutoimitukset.
Esimerkiksi sekaluku "kolme kokonaista ja kaksi viidesosaa" muutetaan murtoluvuksi seuraavasti:
[[$$3\frac{2}{5}=\frac{5\cdot 3+2}{5}=\frac{17}{5}$$]]
Kuinka monta neljäsosapizzaa saadaan leikattua viereisen kuvan pizzoista?
Luvun [[$1$]] murtolukumuoto [[$$1=\frac{n}{n}$$]]
Sekaluvun muuttaminen murtoluvuksi [[$$K\frac{m}{n}=\frac{K\cdot n+m}{n}$$]]
Muodossa [[$\frac{a}{b}$]] esitettyä lukua kutsutaan luvun murtolukuesitykseksi.
Murtoluku tarkoittaa lukua, joka on esitetty murtolukumuodossa. Murtoluku [[$\frac{2}{3}$]] luetaan "kaksi kolmasosaa". Jakoviivan yläpuolista osaa kutsutaan osoittajaksi ja alapuolista osaa nimittäjäksi.
Osoittajasta nähdään, kuinka monta kappaletta kyseisiä osia on, ja nimittäjä ilmaisee yksittäisen osan koon. Esimerkiksi murtoluku [[$\frac{5}{6}$]] tarkoittaa viittä kappaletta kuudesosia, eli
[[$$\frac{5}{6}=5\cdot \frac{1}{6}=\left(\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\right)$$]]
Kokonaisluku voidaan esittää murtolukuna, jonka osoittajana on luku itse ja nimittäjänä luku yksi.
[[$$n=\frac{n}{1}$$]]
Luku yksi voidaan esittää murtolukuna, jolla on sama osoittaja ja nimittäjä.
[[$$1=\frac{n}{n}$$]]
Sekaluku
Joskus ykköstä suuremmat murtoluvut esitetään sekalukuna. Sekaluvussa on kokonaisosa ja murto-osa. Murtolukujen laskutoimitusten yhteydessä on usein selvintä muuttaa kaikki sekaluvut ensin murtoluvuiksi ja sen jälkeen suorittaa laskutoimitukset. Esimerkiksi sekaluku "kolme kokonaista ja kaksi viidesosaa" muutetaan murtoluvuksi seuraavasti:
[[$$3\frac{2}{5}=\frac{5\cdot 3+2}{5}=\frac{17}{5}$$]]
Kuinka monta neljäsosapizzaa saadaan leikattua viereisen kuvan pizzoista?
Murtoluku
Kokonaisluvun murtolukumuoto [[$$n=\frac{n}{1}$$]]Luvun [[$1$]] murtolukumuoto [[$$1=\frac{n}{n}$$]]
Sekaluvun muuttaminen murtoluvuksi [[$$K\frac{m}{n}=\frac{K\cdot n+m}{n}$$]]
Päättymätön jaksollinen desimaaliluku
Kaikki murtoluvut ovat desimaalimuodossa joko päättyviä, tai päättymättömiä, mutta jaksollisia. Toistuva jakso on merkki siitä, että luku voidaan esittää murtolukumuodossa. Esimerkiksi murtoluku [[$\frac{1}{3}= \text{0,3333}...$]]. Toistuva jakso voidaan esittää desimaaliluvussa jakson yläpuolella olevalla viivalla: [[$\text{0,012012}...=\text{0,}\overline{012}$]].Murtolukujen yhteen- ja vähennyslasku
Samankokoisia osia voidaan laskea yhteen ja vähentää
Murtoluvun määritelmästä seuraa, että [[$$\underbrace{ \left(\frac{1}{7}+\frac{1}{7}+\frac{1}{7}\right)}_{\frac{3}{7}} +\underbrace{\left(\frac{1}{7}+\frac{1}{7}\right)}_{\frac{2}{7}}=\frac{5}{7}$$]]Murtolukuja, joilla on sama nimittäjä, kutsutaan samannimisiksi. Samannimisten murtolukujen yhteenlasku suoritetaan laskemalla osoittajien osoittamat määrät yhteen. Nimittäjä säilyy muuttumattomana. Vähennyslasku suoritetaan vastaavalla tavalla.
[[$$\frac{3}{7}+\frac{2}{7}=\frac{3+2}{7}=\frac{5}{7}$$]]
[[$$\frac{3}{7}-\frac{2}{7}=\frac{3-2}{7}=\frac{1}{7}$$]]
Samannimisten murtolukujen yhteen- ja vähennyslasku
Yhteenlasku [[$$\frac{a}{n}+\frac{b}{n}=\frac{a+b}{n}$$]]Vähennyslasku [[$$\frac{a}{n}-\frac{b}{n}=\frac{a-b}{n}$$]]
Laventaminen ja supistaminen
Erinimisiä murtolukuja voidaan laskea yhteen ja vähentää muuntamalla ne ensin samannimisiksi. Murtoluvut ovat samannimiset, jos niiden nimittäjä on sama. Koska samannimiset murtoluvut ilmaisevat samankokoisten osien kappalemääriä, määrät voidaan laskea yhteen. Operaatioita, joilla murtoluvun nimittäjä saadaan muutettua ilman, että luvun lukuarvo muuttuu, ovat laventaminen ja supistaminen. - Laventamisessa kerrotaan osoittaja ja nimittäjä samalla luvulla
- Supistamisessa jaetaan osoittaja ja nimittäjä samalla luvulla
Murtoluvun laventaminen ja supistaminen
Laventaminen luvulla [[$k$]] [[$${\frac{m}{n}=}^{k)}\frac{m}{n}=\frac{k\cdot m}{k \cdot n}$$]]Supistaminen luvulla [[$k$]] [[$$\frac{m}{n}={\frac{m}{n}}^{(k}=\frac{m:k}{n:k}$$]]
Murtolukujen kerto- ja jakolasku
Murtolukujen kertolasku
Murtolukujen kertolasku suoritetaan kertomalla osoittajat keskenään ja nimittäjät keskenään.Jakolasku kertolaskuksi
Kirjoittamalla jakolasku käänteisluvun kertolaskuna, saadaan murtolukujen kerto- ja jakolaskulausekkeista aina muodostettua kertolaskulauseke.Välttääksesi laskuvirheitä, muuta sekaluvut murtoluvuiksi ennen laskemista.
Esimerkiksi
a) [[$5\cdot 3\frac{1}{2} = \dfrac{5}{1} \cdot \dfrac{7}{2}=\dfrac{5\cdot 7}{1\cdot 2}=\dfrac{35}{2}=7\frac{1}{2}$]]
b) [[$4\frac{1}{3}:2\frac{5}{6} = \dfrac{13}{3}: \dfrac{17}{6}=\dfrac{13}{3}\cdot \dfrac{6}{17}={\dfrac{13 \cdot 6}{3\cdot 17}}^{(3}=\dfrac{13 \cdot 2}{17}=\dfrac{26}{17}=1\frac{9}{17} $]]
Murtolukujen kerto- ja jakolasku
Kertolasku [[$$\frac{a}{b}\cdot \frac{c}{d}=\frac{ab}{cd}$$]]Jakolasku [[$$\frac{a}{b}:\frac{c}{d}=\frac{a}{b}\cdot \frac{d}{c}=\frac{ad}{bc}$$]]
Esimerkki 1. Yhteen- ja vähennyslasku
Laske a) [[$\dfrac{1}{3}+\dfrac{1}{4}$]], b) [[$\dfrac{7}{12}-\dfrac{2}{3}$]] ja c) [[$\dfrac{6}{36}+\dfrac{2}{6}$]].
Ratkaisu:
a) [[$\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{4\cdot 1}{4\cdot 3}+\dfrac{3 \cdot 1}{3 \cdot 4}=\dfrac{4}{12}+\dfrac{3}{12}=\dfrac{7}{12}\\$]]
Murtoluvut saadaan samannimisiksi laventamalla ne toistensa nimittäjillä.
b) [[$\dfrac{7}{12}-\dfrac{2}{3}=\dfrac{7}{12}-\dfrac{4\cdot 2}{4 \cdot 3}=\dfrac{7}{12}-\dfrac{8}{12}=-\dfrac{1}{12}\\$]]
Lavennetaan jälkimmäinen luvulla 4, koska [[$12=3\cdot 4$]].
c) [[$\dfrac{6}{36}+\dfrac{2}{6}=\dfrac{6:6}{36:6}+\dfrac{2}{6}=\dfrac{1}{6}+\dfrac{2}{6}=\dfrac{3}{6}=\dfrac{1}{2}\\$]]
Ensimmäinen murtoluku voidaan supistaa luvulla 6, koska [[$36=6\cdot 6$]] ja osoittaja on myös kuudella jaollinen. Lopuksi vielä saatu vastaus on supistettu yksinkertaisimpaan murtolukumuotoon, sillä kolme kuudesosaa on yhtä paljon kuin yksi kahdesosa, eli puoli.
Ratkaisu:
a) [[$\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{4\cdot 1}{4\cdot 3}+\dfrac{3 \cdot 1}{3 \cdot 4}=\dfrac{4}{12}+\dfrac{3}{12}=\dfrac{7}{12}\\$]]
Murtoluvut saadaan samannimisiksi laventamalla ne toistensa nimittäjillä.
b) [[$\dfrac{7}{12}-\dfrac{2}{3}=\dfrac{7}{12}-\dfrac{4\cdot 2}{4 \cdot 3}=\dfrac{7}{12}-\dfrac{8}{12}=-\dfrac{1}{12}\\$]]
Lavennetaan jälkimmäinen luvulla 4, koska [[$12=3\cdot 4$]].
c) [[$\dfrac{6}{36}+\dfrac{2}{6}=\dfrac{6:6}{36:6}+\dfrac{2}{6}=\dfrac{1}{6}+\dfrac{2}{6}=\dfrac{3}{6}=\dfrac{1}{2}\\$]]
Ensimmäinen murtoluku voidaan supistaa luvulla 6, koska [[$36=6\cdot 6$]] ja osoittaja on myös kuudella jaollinen. Lopuksi vielä saatu vastaus on supistettu yksinkertaisimpaan murtolukumuotoon, sillä kolme kuudesosaa on yhtä paljon kuin yksi kahdesosa, eli puoli.
Esimerkki 2. Kerto- ja jakolasku
Laske a) [[$ 3\cdot\dfrac{1}{2} \quad$]] b) [[$ \dfrac{2}{5}\cdot \dfrac{3}{7} \quad$]] c) [[$ \dfrac{1}{2} : \dfrac{1}{2}\quad$]] d) [[$ 5 : \dfrac{1}{3} \quad$]] e) [[$ \dfrac{5}{3} : \dfrac{2}{7}\cdot \dfrac{2}{9} \quad$]] f) [[$\dfrac{5}{3} : 6\quad$]] g) [[$\dfrac{5}{3} : 5\quad$]]
Ratkaisu:
a) [[$ \\ 3\cdot\dfrac{1}{2}=\dfrac{3\cdot 1}{2} =\dfrac{3}{2} \\$]]
Murtoluku voidaan kertoa kokonaisluvulla kertomalla osoittaja kyseisellä luvulla.
b) [[$ \dfrac{2}{5}\cdot \dfrac{3}{7}=\dfrac{2\cdot 3}{5\cdot 7}=\dfrac{6}{35} \\$]]
Murtolukujen tulo lasketaan kertomalla osoittajat ja nimittäjät keskenään.
c) [[$ \\ \dfrac{1}{2} : \dfrac{1}{2}=\dfrac{1}{2} \cdot \dfrac{2}{1}=\dfrac{1\cdot 2}{2 \cdot 1}=\dfrac{2}{2}=1 \\$]]
Luku jaettuna itsellään on yksi.
d) [[$ 5 : \dfrac{1}{3}=5 \cdot \dfrac{3}{1}=5 \cdot 3=15 \\$]]
Murtoluvun jakaminen suoritetaan kertomalla se jakajan käänteisluvulla.
e) [[$ \dfrac{5}{3} : \dfrac{2}{7}\cdot \dfrac{2}{9}=\dfrac{5}{3} \cdot \dfrac{7}{2}\cdot \dfrac{2}{9}=\dfrac{5\cdot 7 \cdot 2}{3 \cdot 2 \cdot 9}=\dfrac{35}{27} \\$]]
Jakolaskutoimitus on käänteisluvulla kertomista.
f) [[$\dfrac{5}{3} : 6=\dfrac{5}{3}\cdot \dfrac{1}{6}=\dfrac{5\cdot 1}{3 \cdot 6}=\dfrac{5}{18} \\$]]
Murtoluku voidaan jakaa kokonaisluvulla kertomalla nimittäjä kyseisellä luvulla.
g) [[$\dfrac{5}{3} : 5=\dfrac{5}{3}\cdot \dfrac{1}{5}=\dfrac{5\cdot 1}{3 \cdot 5}=\dfrac{1}{3} \\$]]
Murtoluku voidaan jakaa kokonaisluvulla jakamalla osoittaja kyseisellä luvulla.
Viimeinen lasku vastaa tilannetta, jossa viisi kappaletta kolmasosia jaetaan viidelle henkilölle. Voidaan päätelläkin, että jokainen saa yhden kolmasosan. Viisi jaettuna viidelle on yksi.
Ratkaisu:
a) [[$ \\ 3\cdot\dfrac{1}{2}=\dfrac{3\cdot 1}{2} =\dfrac{3}{2} \\$]]
Murtoluku voidaan kertoa kokonaisluvulla kertomalla osoittaja kyseisellä luvulla.
b) [[$ \dfrac{2}{5}\cdot \dfrac{3}{7}=\dfrac{2\cdot 3}{5\cdot 7}=\dfrac{6}{35} \\$]]
Murtolukujen tulo lasketaan kertomalla osoittajat ja nimittäjät keskenään.
c) [[$ \\ \dfrac{1}{2} : \dfrac{1}{2}=\dfrac{1}{2} \cdot \dfrac{2}{1}=\dfrac{1\cdot 2}{2 \cdot 1}=\dfrac{2}{2}=1 \\$]]
Luku jaettuna itsellään on yksi.
d) [[$ 5 : \dfrac{1}{3}=5 \cdot \dfrac{3}{1}=5 \cdot 3=15 \\$]]
Murtoluvun jakaminen suoritetaan kertomalla se jakajan käänteisluvulla.
e) [[$ \dfrac{5}{3} : \dfrac{2}{7}\cdot \dfrac{2}{9}=\dfrac{5}{3} \cdot \dfrac{7}{2}\cdot \dfrac{2}{9}=\dfrac{5\cdot 7 \cdot 2}{3 \cdot 2 \cdot 9}=\dfrac{35}{27} \\$]]
Jakolaskutoimitus on käänteisluvulla kertomista.
f) [[$\dfrac{5}{3} : 6=\dfrac{5}{3}\cdot \dfrac{1}{6}=\dfrac{5\cdot 1}{3 \cdot 6}=\dfrac{5}{18} \\$]]
Murtoluku voidaan jakaa kokonaisluvulla kertomalla nimittäjä kyseisellä luvulla.
g) [[$\dfrac{5}{3} : 5=\dfrac{5}{3}\cdot \dfrac{1}{5}=\dfrac{5\cdot 1}{3 \cdot 5}=\dfrac{1}{3} \\$]]
Murtoluku voidaan jakaa kokonaisluvulla jakamalla osoittaja kyseisellä luvulla.
Viimeinen lasku vastaa tilannetta, jossa viisi kappaletta kolmasosia jaetaan viidelle henkilölle. Voidaan päätelläkin, että jokainen saa yhden kolmasosan. Viisi jaettuna viidelle on yksi.
Tutki & Kokeile teknologian avulla
Laske tietokoneella tai laskimella lausekkeiden arvot.
[[$3:6+3:6\\1:3+1:3+1:3\\2:4+3:6\\5:4-1:4\\25:20-5:20\\5\cdot 1:5\\a:3+a:3+a:3\\3\cdot a:3\\a:3+a:3\\a:a$]]
Murtolukujen laskeminen tietokoneella
Murtoluku on jakolasku
 Murtoluvut voidaan syöttää tietokoneelle tai laskimeen käyttämällä vinoviivaa (kauttaviiva) "/". Tällöin suluilla on ilmaistava, mikä osa kuuluu osoittajaan ja mikä nimittäjään. Esimerkiksi [[$(1+2)/(8+9)\neq 1+2/8+9$]].
Murtoluvut voidaan syöttää tietokoneelle tai laskimeen käyttämällä vinoviivaa (kauttaviiva) "/". Tällöin suluilla on ilmaistava, mikä osa kuuluu osoittajaan ja mikä nimittäjään. Esimerkiksi [[$(1+2)/(8+9)\neq 1+2/8+9$]]. Vaihtoehtoisesti lauseke voidaan syöttää matematiikkamalleista löytyvää murtoluku -mallia, jolloin edellistä ongelmaa ei tule.
Tietokoneet ja laskimet eivät hyväksy kaksoispistettä ":" jakolaskun merkintään. Jakolaskun merkkinä kauttaviivan sijaan on useimmissa laskimissa käytössä merkintä "÷".
Sekaluku on kokonaisluvun ja murtoluvun summa
Sekaluku on helpointa syöttää tietokoneelle kokonaisosan ja murto-osan summana. Esimerkiksi [[$3\frac{1}{5}$]] syötetään muodossa "(3+1/5)".GeoGebra
Geogebra -ohjelman CAS-laskennan syöttörivi muokkaa syöttämääsi lauseketta automaattisesti. Tutki ja harjoittele murtolukujen syöttämistä ja laskemista GeoGebran CAS-sovelluksella:http://web.geogebra.org/#cas
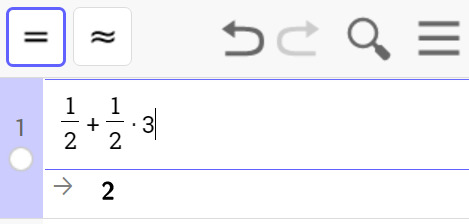
Esimerkki 3
Liitteet:
Esimerkki 4. Päättymätön jaksollinen desimaaliluku murtoluvuksi
Kooste videosta: Päättymätön jaksollinen desimaaliluku murtoluvuksi
Esitä murtolukuna luku [[$ \text{0,11}\overline{392}$]].
Ratkaisu:
[[$$\begin{align}x&=\text{0,11392392}...\\100000x&=\text{11392,392}...\\99900x&=\text{11392,392}...-\text{11,392}...\\x&=\frac{11381}{99900}\end{align}$$]]
Ratkaisu:
[[$$\begin{align}x&=\text{0,11392392}...\\100000x&=\text{11392,392}...\\99900x&=\text{11392,392}...-\text{11,392}...\\x&=\frac{11381}{99900}\end{align}$$]]