Ratkaisut
Monivalintojen vastaukset
Tehtävä 1
Fuusiossa vapautuu energiaa, jos fuusioituvat ytimet ovat niin kevyitä, että sidososuus kasvaa fuusiossa. Näin tapahtuu rautaan saakka. Tällä päättelyllä voidaan vastata a: vapautuu, b: sitoutuu, d: vapautuu. C:n osalta riittää todeta, että pysyvän ytimen purkamiseen tarvitaan aina energiaa, joten purkamisessa energiaa sitoutuu.
Tehtävä 2
Reaktiossa a vapautuu positroni, joten siinä täytyy protonin muuttua neutroniksi ja positroniksi varauksen säilymislain mukaan. Ytimen järjestysluvun pitää tällöin pienentyä yhdellä, mutta se kasvaa. Yhtälö on väärin.
Reaktiossa b on kyse alfahajoamisesta, jolloin järjestysluvun täytyy pienentyä kahdella. Se pienenee vain yhdellä, joten reaktioyhtälö on väärin.
Reaktiossa c vapautuu positroni, joten siinä täytyy protonin muuttua neutroniksi ja positroniksi varauksen säilymislain mukaan. Ytimen järjestysluvun pitää tällöin pienentyä yhdellä, mutta se kasvaa. Yhtälö on väärin.
Reaktiossa d häviää elektroni, joten sen täytyy yhdistyä protonin kanssa ja muodostaa neutroni varauksen säilymislain mukaan. Tällöin ytimen järjestysluvun pitää pienentyä yhdellä, ja näin myös tapahtuu. Myös hiukkasluku säilyy, alun protoni ja elektroni muuttuvat neutroniksi ja neutriinoksi. Yhtälö esittää elektronisieppausta, ja Fe-55 hajoaa sen kautta. Yhtälö on oikein.
Reaktiossa e on kyse spontaanista fissiosta. Nukleonien kokonaismäärä säilyy (254), ja myös protonien määrä säilyy (98). Yhtälö on oikein.
Reaktiossa f on kyse alfahajoamisesta, jolloin järjestysluvun täytyy pienentyä kahdella. Näin myös tapahtuu, ja massaluku pienenee neljällä. Yhtälö on teknisesti oikein, mutta Ba-139 ei hajoa alfakanavan kautta ja siten yhtälö on väärä.
Tehtävä 3 ratkaisu
Alla on erään beetahajoamisen energiatasokaavio.
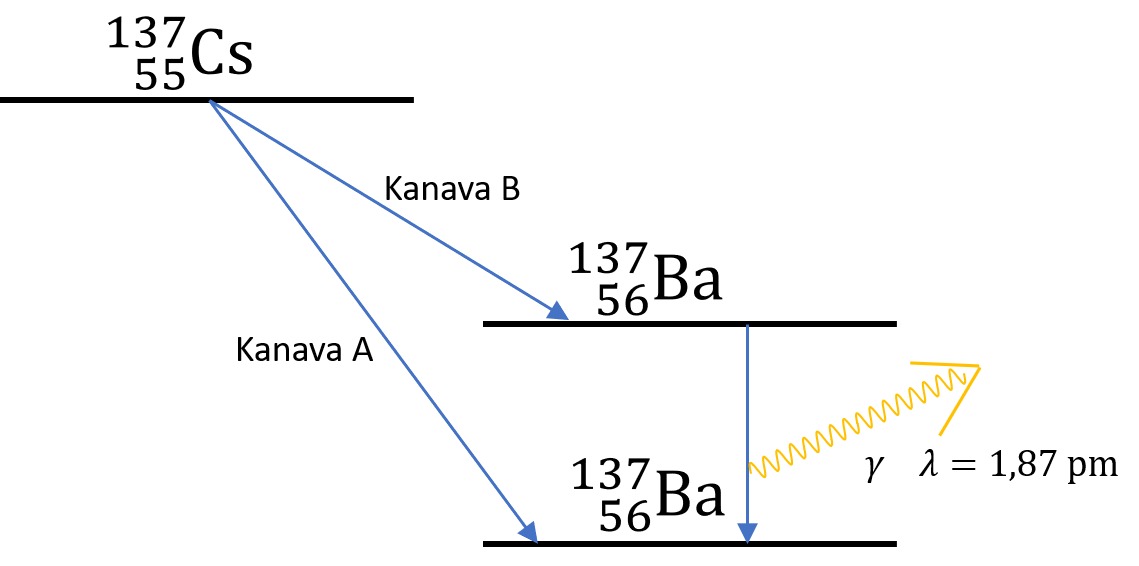
a) Paljonko tässä beetahajoamisessa vapautuu yhteensä energiaa? (3 p.)
b) Mihin tämä energia menee? Tarkastele erikseen hajoamiskanavia A ja B ja jos mahdollista laske, paljonko energiaa mihinkin kohteeseen menee. (5 p.)
a) Vapautuva energia saadaan laskemalla, paljonko massaa reaktiossa vapautuu energiaksi: [[$E=\Delta mc^2$]]. Reaktioyhtälö on
[[$^{137}_{\,\,55}\text{Cs}\rightarrow{^{137}_{\,\,56}\text{Ba}}+\text{e}+\overline{\nu}$]]
Reaktioyhtälö päätelty oikein, 1p
Vapautuvaksi energiaksi saadaan
[[$\begin{align*}E&=\left(\left(m_\text{Cs-atomi}-55m_\text{e}\right)-\left(m_\text{Ba-atomi}-56m_\text{e}\right)-m_\text{e}\right)c^2\\&=\left(136,907073\text{ u}-136,905812\text{ u}\right)\cdot 931,494102\text{ MeV/u}\\&=1,1746\dots\text{MeV}\approx 1,175\text{ MeV}\\ \end{align*}$]]
Periaate oikein 1p
Lukuarvot ja vastaus oikein 1p
b) Hajoamisessa syntyy elektroni, tytärydin ja antineutriino. Kanavassa A koko vapautuva energia muuttuu näiden liike-energiaksi.
Kanava A hahmotettu oikein 1p
Kanavassa B syntyvä tytärydin jää viritystilaan, jonka purkautuessa emittoituu 1,87 pm aallonpituudeltaan oleva fotoni. Liike-energiaksi muuttuu siis vähemmän kuin kanavassa A.
Kanava B hahmotettu oikein 1p
Emittoituvan fotonin energia on
[[$E_\gamma=\dfrac{hc}{\lambda}=\dfrac{1240\text{ eV nm}}{0,00187\text{ nm}}=663,1\dots\text{keV}\approx 663\text{ keV}$]]
Fotonin energian kaava 1p
Fotonin energia oikein 1p
Kanavassa B liike-energiaksi jää siis noin [[$1,175\text{ MeV}-0,663\text{ MeV}=0,512\text{ MeV}$]]
Oikea johtopäätös 1p
Tehtävä 4 ratkaisu
Erään radioaktiivisen näytteen aktiivisuutta mitattiin ajan funktiona. Tulokset ovat oheisessa aineistossa.
a) Määritä hajoamisvakio ja puoliintumisaika. (5 p.)
b) Missä ajassa aktiivisuus laskee alle promilleen alkuperäisestä? (3 p.)
a) Esitetään aktiivisuus graafisesti ajan funktiona:
Onnistunut graafinen esitys, 1 p.
Havaitaan, että tulokset noudattavat hajoamislakia [[$A(t)=A_0e^{-\lambda t}$]]. Sovituksesta nähdään, että hajoamisvakio on
[[$\lambda= 0,01438\dots\text{1/min}\approx 0,000239667\text{ 1/s}$]]
Perusteluna hajoamislaki, 1 p.
Hajoamisvakio oikein, 1 p.
Puoliintumisaika saadaan tästä:
[[$T_{1/2}=\dfrac{\ln 2}{\lambda}=\dfrac{\ln 2}{0,000239667\text{ 1/s}}=2892,1\dots\text{s}\approx 48\text{ min}$]]
Puoliintumisajan ja hajoamisvakion yhteys, 1 p.
Puoliintumisaika oikein, 1 p.
b) On ratkaistava yhtälö [[$A(t)=0,001A_0$]]. Ratkaistaan:
Yhtälö oikein, 1p.
[[$\begin{align*}0,001A_0&=A_0e^{-\lambda t}\\ 0,001&=e^{-\lambda t}\\ \ln 0,001&=-\lambda t\\ t&=\dfrac{\ln 0,001}{-\lambda}\\&=\dfrac{\ln 0,001}{-0,000239667\text{ 1/s}}=28822,3\dots\text{s}\approx 8,0 \text{ h}\\ \end{align*}$]]
Oikea vastaus, 2 p.
(Vähinen virhe ja väärä vastaus, 1 p.)
