1.2 Aaltohiukkasdualismi
Kvanttien eli fotonien liikemäärä
Valosähköilmiö osoittaa sähkömagneettisen säteilyn energian siirtyvän kvantteina. Tällaisen kvantin vakiintuneeksi nimeksi on muodostunut fotoni.
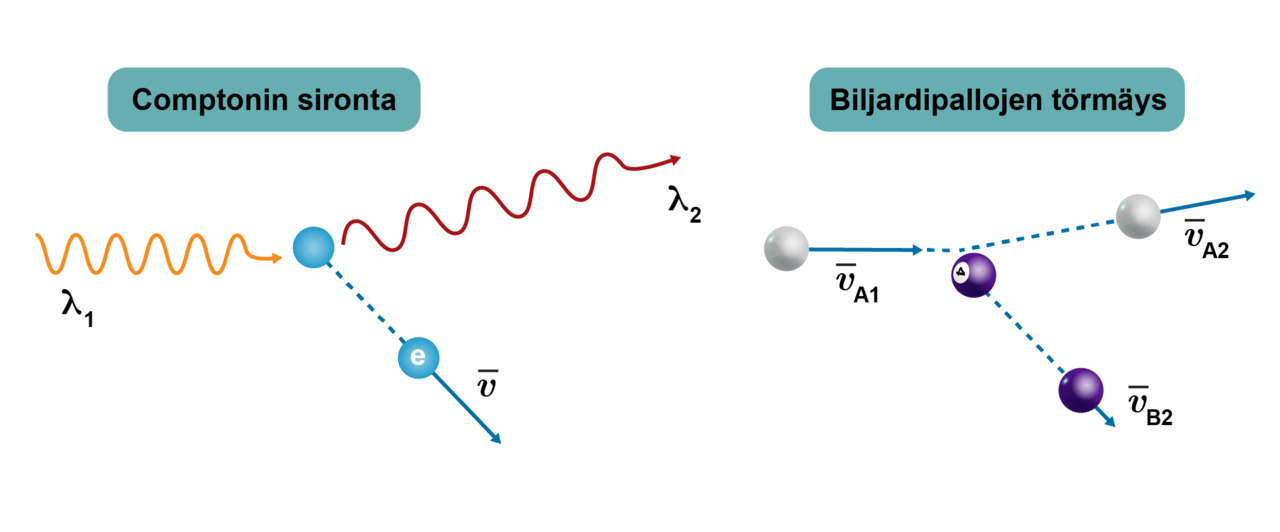
Energian lisäksi fotoneilla on liikemäärä, vaikka niillä ei ole massaa. Fotonien liikemäärä havaitaan säteilyn absorptiossa, emissiossa sekä erityisesti röntgen- tai gammasäteilyn sirotessa elektronista. Jälkimmäistä ilmiötä kutsutaan Comptonin sironnaksi sitä tutkineen Nobel-palkitun Arthur Comptonin (1892–1962) mukaan.
Comptonin sironnassa fotonien energia on huomattavasti suurempi kuin niiden energia valosähköilmiössä, jolloin irrotustyö on fotonien energiaan nähden merkityksettömän pieni. Elektroneja voidaan siksi tarkastella kuin ne olisivat vapaita hiukkasia. Röntgen- tai gammasäteilyn osuessa levossa olevaan elektroniin ja sirotessa eri suuntaan sen aallonpituus pitenee. Tilanne voidaan tulkita energian säilymisen kannalta niin, että fotoni absorboituu luovuttaen koko energiansa elektronille, jonka jälkeen osa energiasta vapautuu uutena fotonina. Elektroni saa fotonien energian erotuksen verran liike-energiaa. Elektronin saama liike-energia on yhtä suuri kuin fotonien energioiden erotus.
[[$\qquad E_\text{e}=E_{\lambda_1}-E_{\lambda_2}$]]
Liike-energian myötä elektroni on saanut myös liikemäärän [[$p = mv$]], jossa [[$m$]] on elektronin massa ja [[$v$]] elektronin nopeus. Liikemäärä säilyy myös vuorovaikutustilanteissa, joten fotoni-elektroni-systeemin kokonaisliikemäärän täytyy olla sama ennen ja jälkeen sironnan. Elektronin saaman liikemäärän täytyy siis olla sama kuin fotonien liikemäärävektorien erotus:
[[$\qquad \overline{p}_\text{e}=\overline{p}_{\lambda_1}-\overline{p}_{\lambda_2}$]]
Tarkemmin mitatessa on todettu fotonin liikemäärän olevan lausekkeen [[$ p=\dfrac {h}{\lambda} $]] mukainen, kun [[$h$]] on Planckin vakio ja [[$\lambda$]] fotonin aallonpituus.
Huomaa, että tutkittaessa elektronin saamaa energiaa ja liikemäärää Comptonin sironnassa energian säilyminen tuottaa yksinkertaisemman yhtälön. Liikemäärä on vektori, joten liikemäärän säilymisessä tulisi ottaa huomioon sironneen elektronin ja emittoituneen fotonin suunta, mikä ei kuulu lukiossa käsiteltäviin asioihin. Energia ei ole vektori, jolloin energiaperiaateyhtälössä suuntia ei tarvitse ottaa huomioon.
Comptonin sirontaa voidaan verrata makroskooppisessa maailmassa tapahtuvaan biljardipallojen törmäykseen, jossa liike-energia ja liikemäärä säilyvät.
Fotonin liikemäärä
Fotonilla on liikemäärä [[$ p $]], joka on kääntäen verrannollinen aallonpituuteen [[$ \lambda $]]:
[[$ \qquad p=\dfrac {h}{\lambda}$]]
Tässä [[$ h $]] on Planckin vakio, [[$ h=6{,}62606957 \cdot 10^{-34} \text{ Js}$]]
Valosähköilmiö ja Compotonin sironta ovat esimerkkejä siitä, että sähkömagneettinen säteily käyttäytyy tietyissä vuorovaikutustilanteissa kuten hiukkanen.
Sähkömagneettinen säteily – aaltoja ja hiukkasia
Valon luonnetta kuvaava teoria on tarkentunut useaan otteeseen tieteen historiassa. Muun muassa Isaac Newtonin näkemys oli, että valo koostuu hiukkasista. 1800-luvulla sähkömagnetismin teoria antoi valolle tarkan selityksen sähkömagneettisena aaltoliikkeenä, mistä muodostui joksikin aikaa hallitseva näkemys hiukkasmallin sijaan. Säteilyn kvantittumisen teoria ja käsitys fotoneista muodostui 1900-luvun alkuvuosina. Monissa mittauksissa fotonit ovat osoittautuneet todellisiksi ja niiden avulla selitetään nykyfysiikassa kattavasti sähkömagneettinen vuorovaikutus.
Fotoneista huolimatta ei ole palattu Newtonin käsitykseen valosta yksipuolisesti hiukkasina, sillä sähkömagneettisen säteilyn aaltoluonteen mukaiset ilmiöt, kuten interferenssi ja polarisaatio, ovat edelleen todellisuutta. Fotoneja kuvaavasta kvanttiteoriasta onkin tullut klassista sähkömagnetismia laajentava teoria. Monet valon makroskooppisen tason ilmiöt ovat ymmärrettävissä valon aaltomallin kautta, mutta mikroskooppisen tason selityksessä fotonien olemassaolo on välttämätön. Sähkömagneettinen säteily on luonteeltaan dualistista. Sillä on sekä aaltomaisia että hiukkasmaisia ominaisuuksia.
Kaksoisrakokoe on osoitus valon aaltoluonteesta. Resonanssi 7 -oppikirjassa tutkittiin valon kulkua kaksoisraon tai hilan läpi. Näissä kokeissa valo tuottaa varjostimelle interferenssikuvion, joissa havaitaan yksittäisiä kirkkaita pisteitä, intensiteettimaksimeja.
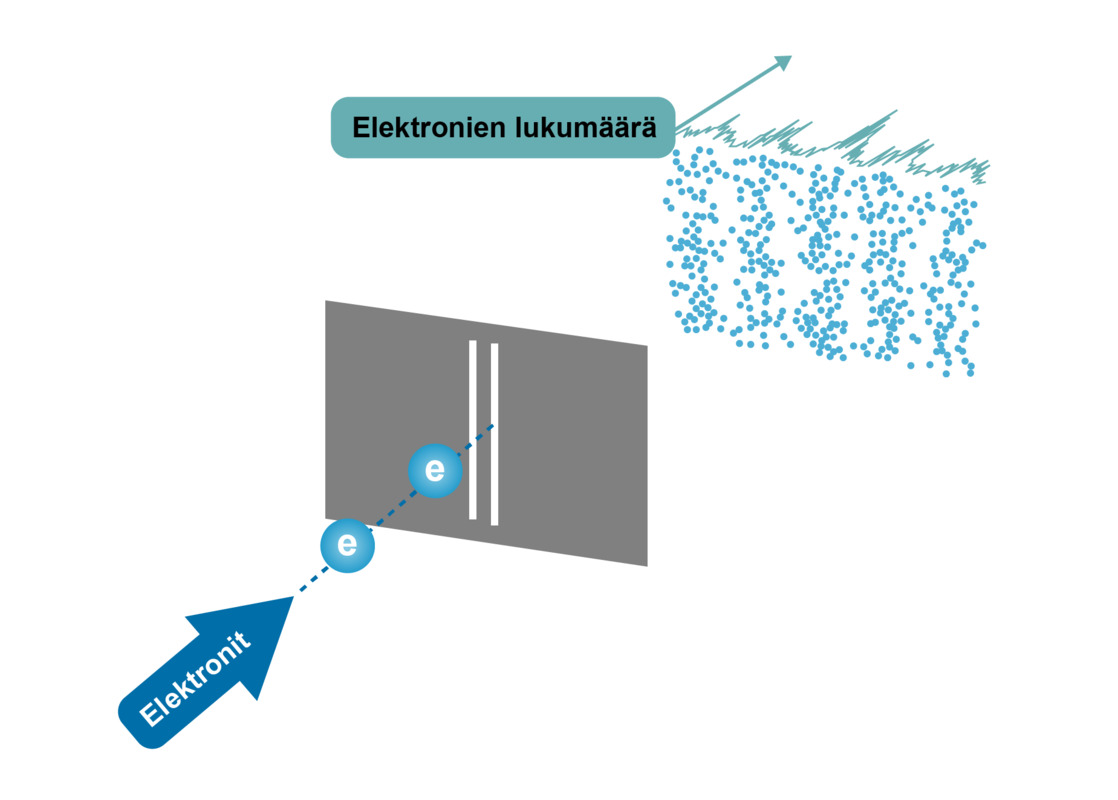
Moderneilla mittalaitteilla toteutettuna kaksoisrakokoe paljastaa valon dualistisen luonteen. Kun hilaan kohdistetaan hyvin heikkoa valoa, havaitaan valon absorboituvan mittalaitteeseen yksittäisinä fotoneina, hiukkasmaisesti. Vasta kun yksittäisiä fotoneja on kertynyt paljon, havaitaan niiden muodostama aalloille ominainen interferenssikuvio.
Havainto tulkitaan siten, että jokainen fotoni käyttäytyy aallon tavoin raosta kulkiessaan. Fotoni kulkee molemmista raoista, interferoi itsensä kanssa ja paikantuu tiettyyn pisteeseen.
Vaikka fotonista voidaan puhua "hiukkasena, joista valo koostuu", se ei ole samanlainen hiukkanen kuin muut. Fotoniin ei voi tarttua, sitä ei voi siirtää, hidastaa tai kiihdyttää. Fotoni liikkuu aina valon nopeudella, ja sen tavat vuorovaikuttaa aineen kanssa ovat vain syntyminen (emissio) ja tuhoutuminen (absorptio). Näissä tapahtumissa fotoni joko saa tai luovuttaa energiansa ja liikemääränsä kokonaan sille hiukkaselle, joka sen emittoi tai absorboi.
Suuri määrä fotoneja käyttäytyy etenevän aaltorintaman tavoin, mutta yksittäisellä fotonillakin on aaltoluonne. Tarkan paikan sijaan fotonin sijaintia kuvaa aalto, joka ilmaisee fotonin sijainnin todennäköisyyksiä tietyllä hetkellä. Klassisen hiukkasen sijaan fotoneita ilmentää paremmin aaltopaketti, jossa yhdistyvät hiukkasmaiset ja aaltomaiset ominaisuudet.
Kaksoisrakokoe elektroneilla
Klassinen malli käsittelee elektroneja ja muita alkeishiukkasia sokerikiteiden kaltaisina pistemäisinä kappaleina. Jos sokeria pudotetaan levylle, jossa on lähekkäin kaksi rakoa, suurin osa kiteistä kertyy levyn alle suoraan rakojen alapuolelle. Alla on kuva tilanteesta. Klassisen mallin mukaan elektronien kaksoisrakokokeessa kummankin raon taakse tulisi syntyä elektroniosumien keskittymät sokerikasojen tapaan. Kun koe suoritetaan, näin ei kuitenkaan tapahdu.
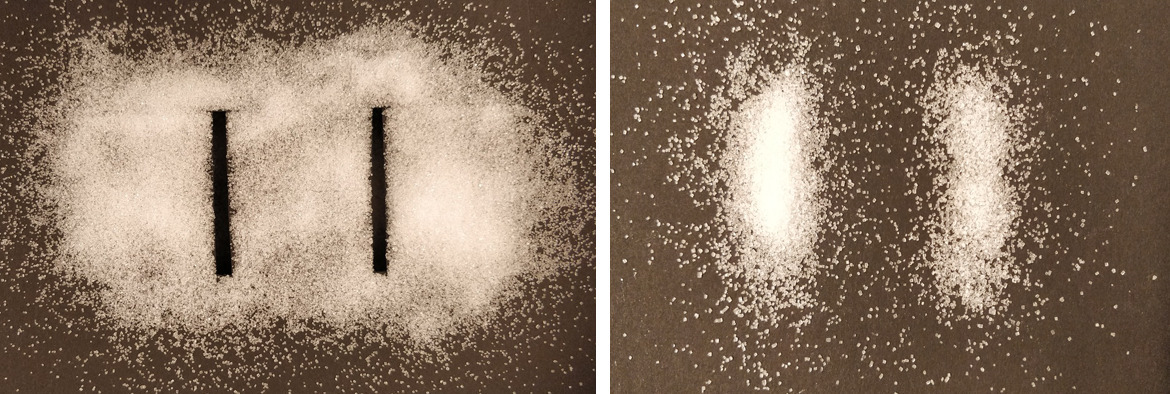
Elektronien kaksoisrakokokeessa syntyy samanlainen kuvio kuin kaksoisraon läpi kulkeneen valon tapauksessa. Elektronien osumakohtia on vuoroin lähekkäin ja vuoroin harvassa. Tämä osoittaa elektronien käyttäytyvän kaksoisraossa aallon kaltaisesti. Raosta kulkevat elektronit interferoivat kuin ne olisivat aaltoja, ja varjostimelle syntyy maksimi- ja minimikohtia sen mukaan, onko interferenssi vahvistava vai heikentävä.
Jotta havaitaan, onko aaltomaisuus yksittäisen elektronin vai usean elektronin muodostaman joukon ominaisuus, täytyy tarkkailla elektronien kertymistä varjostimelle yksi kerrallaan. Alla on kuvasarja, jossa valkoiset pisteet ovat yksittäisten elektronien osumakohtia varjostimella. Kuvat on otettu 11, 200, 6 000, 40 000 ja 140 000 elektronin jälkeen. Havaitaan, että yksittäiset elektronit osuvat varjostimella näennäisesti minne sattuu, mutta elektronien määrän lisääntyessä osumakohdista muodostuu aaltoliikkeelle ominainen interferenssikuvio. Yksittäinen elektroni osuu todennäköisimmin sinne, missä raoista kulkeneet aallot vahvistavat toisiaan. Aaltomaisuus on näin ollen yksittäisen elektronin ominaisuus, aivan kuten fotoneillakin. Yksittäisen elektronin osumakohtaa ei voida määrittää, mutta interferenssikuvio ennustaa, mihin se todennäköisimmin osuu.
de Broglie -aallonpituus
Ranskalainen Louis de Broglie (1892–1987) esitti vuonna 1923 hypoteesin hiukkasen aaltoluonteesta ennen kokeellisia havaintoja. Hypoteesi syntyi, kun valon kaksoisluonne oli havaittu valosähköisen ilmiön ja Comptonin sironnan perusteella. Tiedettiin, että fotonilla on liikemäärä, joka riippuu valon aallonpituudesta: [[$p=\dfrac{h}{\lambda}$]]. de Broglie esitti, että sama kaava toisinpäin käytettynä ilmaisisi hiukkasen aallonpituuden: [[$\lambda=\dfrac{h}{p}=\dfrac{h}{mv}$]]. Ensimmäinen vahvistus de Broglien hypoteesille saatiin tarkastelemalla elektronien siroamista nikkelihilasta vuonna 1927. Sittemmin hypoteesi on vahvistettu useissa eri tilanteissa.
Hiukkasen de Broglien aallonpituus
[[$ \lambda=\dfrac{h}{mv}$]] on nopeudella [[$v$]] liikkuvan [[$m$]]-massaisen hiukkasen aallonpituus. [[$h$]] on Planckin vakio. Jotta aallonpituuden saa metreinä, Planckin vakiota on käytettävä yksiköissä Js.Aaltomaisuus on yleensä sitä helpompi havaita, mitä suurempi aallonpituus on. Jotta aallon havaitaan leviävän merkittävästi kulkiessaan rakojen läpi, on aallonpituuden ja raon leveyden oltava samaa suuruusluokkaa. Äänelle riittää oven kokoinen rako, mutta valolle rako saa olla enintään mikrometrien suuruusluokkaa.
Lasketaan de Broglien aaltojen suuruusluokan hahmottamiseksi 100 V jännitteellä kiihdytetyn elektronin aallonpituus. Tällä jännitteellä kiihdytetyn elektronin nopeus on suuruusluokkaa 107 m/s, jolloin aallonpituudeksi saadaan
[[$ \begin{align*}\quad \lambda &=\dfrac{h}{mv} \\ \\ \lambda &=\dfrac{6{,}626\cdot 10^{-34}\text{ m}^2\text{kg/s}}{9{,}109\cdot 10^{-31}\text{ kg}\cdot 10^7\text{ m/s}} \\ \\ \lambda &=7{,}27\dotso\cdot 10^{-11}\text{ m}\approx 0{,}07\text{ nm}\end{align*}$]]
Liikkuvan elektronin aaltomaisuuden havaitsemiseen aallon taipumisen kautta tarvitaan erittäin ohut rako, ohuempi kuin valolle. de Broglien aallonpituuden kaavasta havaitaan, että hiukkasen aallonpituus on sitä suurempi, mitä kevyempi se on ja mitä hitaammin se liikkuu. Elektronista kevyempiä alkeishiukkasia ei oikeastaan ole tarjolla, joten ainoaksi vaihtoehdoksi aallonpituuden kasvattamiseen jää hiukkasten hidastaminen. Aaltomaisuuden havaitseminen muilla kuin hitaasti liikkuvilla alkeishiukkasilla on suuri kokeellinen haaste, ja makroskooppisilla kappaleilla aaltomaisuuden havaitseminen on käytännössä mahdotonta.
Esimerkkitilanne: de Broglien aallonpituus ja kaksoisrakokoe
Tarkastellaan kaksoisraon läpi varjostimelle kulkevien elektronien muodostamaa interferenssikuviota. Elektroneja kertyy eniten niihin kohtiin, joissa raoista tulleet aallot vahvistavat toisiaan. Tällöin aaltojen on oltava samassa vaiheessa, eli matkaeron tulee olla kokonainen määrä aallonpituuksia, [[$k\lambda$]], missä [[$k=0,1,2,\ldots$]] Matkaero puolestaan on [[$d\sin\theta,$]] missä [[$d$]] on rakojen etäisyys toisistaan ja [[$\theta$]] on kulma, jossa maksimi sijaitsee. Hilayhtälö on täsmälleen sama kuin valolle: [[$k\lambda=d\sin\theta$]].
Hilayhtälön mukaan maksimit syntyvät kulmiin.
[[$ \qquad\begin{align} \sin \theta &=\dfrac{k\lambda}{d}\\ \theta_k&=\arcsin\dfrac{k\lambda}{d}\end{align}$]]
Kulmat ovat sitä pienempiä, mitä pienempi aallonpituus on. Erittäin pienillä aallonpituuksilla maksimeja ei erota toisistaan, eikä interferenssikuviota havaita. de Broglien kaavan mukaan aallonpituus on sitä suurempi, mitä kevyemmästä hiukkasesta on kyse ja mitä hitaammin se liikkuu. Kaksoisrakokokeen onnistumisen kannalta elektronit eivät kuitenkaan voi liikkua miten hitaasti tahansa. Elektroneilla on varaus, joten ne ovat alttiita sähkömagneettisille vuorovaikutuksille, eivätkä kulje suoraan kohti rakoa. Tämä tekee kokeen käytännön järjestelystä vaikeaa: elektronit on ammuttava riittävän suurella nopeudella, mutta tällöin interferenssikuvio pienenee ja sen havaitseminen on haasteellisempaa. Kokeen onnistui toteuttamaan ensimmäisen kerran saksalainen Claus Jönsson v. 1961.
Toistaiseksi interferenssikuvio on onnistuttu havaitsemaan kaksoisrakokokeessa elektronien lisäksi esim. protoneilla ja joillakin molekyyleillä. Massiivisin molekyyli, jolla tässä on onnistuttu, on eräs orgaaninen yhdiste. Molekyylin massa on n. 10 000 -kertainen protonin massaan nähden. Näin ollen de Broglien hypoteesin voidaan katsoa osoitetun todeksi myös atomia selvästi suuremmille hiukkasille.
Pysähdy pohtimaan
Esimerkkejä
Esimerkki 2
Comptonin sironnassa fotoni, jonka aallonpituus on 8,5 nm, osuu vapaaseen elektroniin. Elektronista siroavan fotonin aallonpituus on 21 nm. Laske, kuinka suuren energian elektroni saa.
Esimerkki 3
Auringon valon intensiteetti Maassa on 1300 W/m2. Oletetaan valon keskimääräiseksi aallonpituudeksi 510 nm. Laske voima, jonka valo kohdistaa absorboituessaan lierihattuun, jonka pinta-ala on 0,071 m2.
Esimerkki 4
Ammuttaessa elektroneja kaksoisraon läpi varjostimelle päämaksimin molemmille puolille muodostui sivumaksimit 2,8 cm:n päähän. Varjostin oli 97 cm:n päässä kaksoisraosta. Kaksoisraon rakojen etäisyys toisistaan oli 200 nm.
- Laske elektronien de Broglien aallonpituus.
- Laske elektronien nopeus ja kiihdyttämiseen vaadittu jännite.
- Miten tilanne muuttuu, jos elektronien nopeutta kasvatetaan tai pienennetään?
Esimerkki 5
Tarkimmat elektronimikroskoopit (katso tietolaatikko) pystyvät erottamaan 50 pikometrin kokoisia yksityiskohtia. Laske tällaisen elektronimikroskoopin käyttämien elektronien nopeus ja jännite, jolla elektronit tulee kiihdyttää. Miten tilanne muuttuu, jos elektronien nopeutta suurennetaan tai pienennetään?