Muuttuva liike
Kuten 1. kappaleessa todettiin, niin liike on harvoin tasaista. Liikettä, jossa nopeus tai liikkeen suunta muuttuu, kutsutaan kiihtyväksi. Esimerkiksi oppilastyössä kaltevaa tasoa pitkin liukuvan metallikuulan liike on kiihtyvää, sillä sen nopeus kasvaa koko ajan. Myös mutkittelevan auton liike on kiihtyvää, sillä liikkeen suunta muuttuu.
Kiihtyvän liikkeen aiheuttaa aina jokin voima. Auto kiihtyy vain, jos moottori synnyttää tarpeeksi suuren voiman voittaakseen kitkan. Putoava kappale on kiihtyvässä liikkeessä, sillä Maan painovoima saa kappaleen nopeuden kasvamaan. Palaamme erilaisiin voimiin seuraavassa kappaleessa.
Planeettojen liike on kiihtyvää, sillä niiden suunta muuttuu jatkuvasti ympyränmuotoisella kiertoradalla.
Keskikiihtyvyyden laskeminen
Kiihtyvyys kertoo, kuinka voimakkaasti kappaleen nopeus muuttuu, eli kiihtyvyys voidaan laskea jos tiedetään nopeuden muutos tietyssä aikayksikössä. Keskikiihtyvyys kertoo, kuinka nopeus keskimäärin muuttuu tietyllä aikavälillä.
Kiihtyvyyden tunnus on [[$a$]] (acceleration) ja kiihtyvyyden yksikkö on [[$\frac{m}{s^2}$]]. Jos kappaleen keskikiihtyvyys on esimerkiksi 5[[$\frac{m}{s^2}$]], niin silloin kappaleen nopeus kasvaa keskimäärin 5[[$\frac{m}{s}$]] joka sekunti.
Koska kiihtyvyyden suuruuden määrää nopeuden muutos tietyssä ajassa, niin keskikiihtyvyys voidaan laskea kaavalla [[$$keskikiihtyvyys=\frac{nopeuden \ muutos}{ajan \ muutos}$$]] eli [[$$a=\frac{\Delta \ v}{\Delta \ t}.$$]]
Putoamiskiihtyvyys
Maapallon painovoima aiheuttaa kaikille putoaville kappaleille putoamiskiihtyvyyden [[$g$]]. Putoamiskiihtyvyyden [[$g$]] suuruus on likimain [[$g=10\frac{m}{s^2}$]]. Jos pudotat kiven korkealta, niin ensimmäisen sekunnin jälkeen kiven nopeus on [[$10\frac{m}{s}$]], toisen sekunnin jälkeen [[$20\frac{m}{s}$]] ja niin edelleen. Kun nopeus kasvaa riittävän suureksi, niin ilmanvastus pienentää nopeuden kasvua.
HUOM! Putoamiskiihtyvyyden [[$g$]] tarkempi ja yleisemmin käytetty arvo on [[$g=9,81\frac{m}{s^2}$]], mutta me tyydymme likiarvoon [[$g\approx 10\frac{m}{s^2}$]].
Kiihtyvyydestä puhuttaessa käytetään usein yksikkönä "g:tä". Yksi g tarkoittaa yhtä Maapallon putoamiskiihtyvyyttä eli [[$1 \ g=10\frac{m}{s^2}$]]. Esimerkiksi formulakuskit ja hävittäjälentäjät joutuvat kestämään valtavia g-voimia suurissa nopeuksissa tehdyistä käännöksistä johtuen. Formuloissa g-voimat saattavat yltää hetkellisesti jopa 5 g:hen asti, jolloin kuljettaja tuntee itsensä viisi kertaa normaalia painavammaksi.
Päästäkseen avaruuteen avaruussukkulan kiihtyvyyden tulee olla tarpeeksi suuri. Kantoraketit on suunniteltu siten, että niiden tuottama kiihtyvyys on enimmilllään [[$3 \ g \approx 30 \frac{m}{s^2}$]].
Kiihtyvyys koordinaatistossa
Viime kappaleessa opimme, että tasaisen liikkeen kuvaaja aika-matka-koordinaatistossa on suora viiva. Oppilastyössä tutkiessasi metallikuulan liikettä huomasit, että kuulan liike aika-matka-koordinaatistossa ei ollutkaan suora viiva, vaan ylöspäin nouseva käyrä. Kiihtyvän liikkeen kuvaajan kaarevuus aika-matka-koordinaatistossa johtuu siitä, että ajan kuluessa nopeus kasvaa, jolloin tietyssä ajassa kuljetaan yhä pidempi matka.
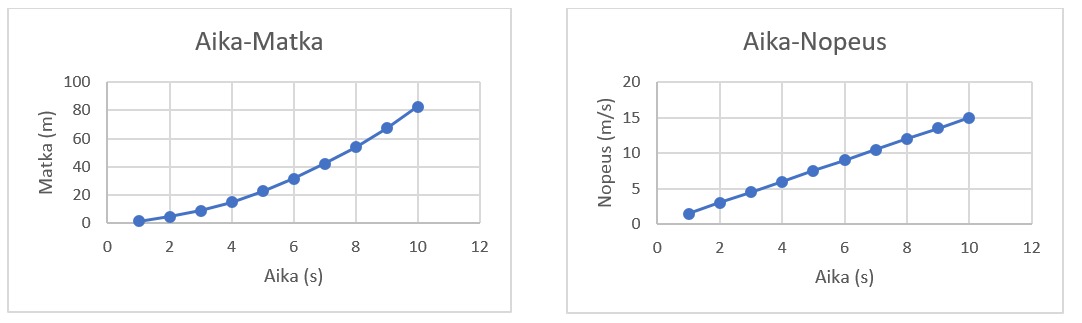Yllä olevissa kuvaajissa on esitetty sama tasaisesti kiihtyvä liike aika-matka- ja aika-nopeus-koordinaatistoissa. Aika-matka-koordinaatiston kuvaaja on ylöspäin nouseva käyrä ja aika-nopeus-koordinaatiston kuvaaja on nouseva suora.
Kiihtyvän liikkeen aiheuttaa aina jokin voima. Auto kiihtyy vain, jos moottori synnyttää tarpeeksi suuren voiman voittaakseen kitkan. Putoava kappale on kiihtyvässä liikkeessä, sillä Maan painovoima saa kappaleen nopeuden kasvamaan. Palaamme erilaisiin voimiin seuraavassa kappaleessa.
Planeettojen liike on kiihtyvää, sillä niiden suunta muuttuu jatkuvasti ympyränmuotoisella kiertoradalla.Keskikiihtyvyyden laskeminen
Kiihtyvyys kertoo, kuinka voimakkaasti kappaleen nopeus muuttuu, eli kiihtyvyys voidaan laskea jos tiedetään nopeuden muutos tietyssä aikayksikössä. Keskikiihtyvyys kertoo, kuinka nopeus keskimäärin muuttuu tietyllä aikavälillä.
Kiihtyvyyden tunnus on [[$a$]] (acceleration) ja kiihtyvyyden yksikkö on [[$\frac{m}{s^2}$]]. Jos kappaleen keskikiihtyvyys on esimerkiksi 5[[$\frac{m}{s^2}$]], niin silloin kappaleen nopeus kasvaa keskimäärin 5[[$\frac{m}{s}$]] joka sekunti.
Koska kiihtyvyyden suuruuden määrää nopeuden muutos tietyssä ajassa, niin keskikiihtyvyys voidaan laskea kaavalla [[$$keskikiihtyvyys=\frac{nopeuden \ muutos}{ajan \ muutos}$$]] eli [[$$a=\frac{\Delta \ v}{\Delta \ t}.$$]]
| Esimerkki Auto lähti paikoiltaan ja viiden sekunnin kuluttua sen nopeus oli 20 [[$\frac{m}{s}$]]. Lasketaan auton keskikiihtyvyys. Nopeuden muutos [[$\Delta v=20\frac{m}{s}$]] ja ajan muutos [[$\Delta \ t=5 \ s$]], joten keskikiihtyvyys [[$a$]] on [[$$a=\frac{\Delta v}{\Delta t}= \frac{20\frac{m}{s}}{5s} =4 \ \frac{m}{s^2}.$$]] |
Putoamiskiihtyvyys
Maapallon painovoima aiheuttaa kaikille putoaville kappaleille putoamiskiihtyvyyden [[$g$]]. Putoamiskiihtyvyyden [[$g$]] suuruus on likimain [[$g=10\frac{m}{s^2}$]]. Jos pudotat kiven korkealta, niin ensimmäisen sekunnin jälkeen kiven nopeus on [[$10\frac{m}{s}$]], toisen sekunnin jälkeen [[$20\frac{m}{s}$]] ja niin edelleen. Kun nopeus kasvaa riittävän suureksi, niin ilmanvastus pienentää nopeuden kasvua.
HUOM! Putoamiskiihtyvyyden [[$g$]] tarkempi ja yleisemmin käytetty arvo on [[$g=9,81\frac{m}{s^2}$]], mutta me tyydymme likiarvoon [[$g\approx 10\frac{m}{s^2}$]].
Kiihtyvyydestä puhuttaessa käytetään usein yksikkönä "g:tä". Yksi g tarkoittaa yhtä Maapallon putoamiskiihtyvyyttä eli [[$1 \ g=10\frac{m}{s^2}$]]. Esimerkiksi formulakuskit ja hävittäjälentäjät joutuvat kestämään valtavia g-voimia suurissa nopeuksissa tehdyistä käännöksistä johtuen. Formuloissa g-voimat saattavat yltää hetkellisesti jopa 5 g:hen asti, jolloin kuljettaja tuntee itsensä viisi kertaa normaalia painavammaksi.
Päästäkseen avaruuteen avaruussukkulan kiihtyvyyden tulee olla tarpeeksi suuri. Kantoraketit on suunniteltu siten, että niiden tuottama kiihtyvyys on enimmilllään [[$3 \ g \approx 30 \frac{m}{s^2}$]].Kiihtyvyys koordinaatistossa
Viime kappaleessa opimme, että tasaisen liikkeen kuvaaja aika-matka-koordinaatistossa on suora viiva. Oppilastyössä tutkiessasi metallikuulan liikettä huomasit, että kuulan liike aika-matka-koordinaatistossa ei ollutkaan suora viiva, vaan ylöspäin nouseva käyrä. Kiihtyvän liikkeen kuvaajan kaarevuus aika-matka-koordinaatistossa johtuu siitä, että ajan kuluessa nopeus kasvaa, jolloin tietyssä ajassa kuljetaan yhä pidempi matka.
Yllä olevissa kuvaajissa on esitetty sama tasaisesti kiihtyvä liike aika-matka- ja aika-nopeus-koordinaatistoissa. Aika-matka-koordinaatiston kuvaaja on ylöspäin nouseva käyrä ja aika-nopeus-koordinaatiston kuvaaja on nouseva suora.