Yhtälön ratkaisemista ohjelmoinnin avulla
Tämän sivun tehtävien tarkoituksena on käyttää ohjelmointia yhtälöiden ratkaisemiseen. Tämän sivun alasivujen teoria ja harjoitukset auttavat käyttäjää lopulta ohjelmoimaan ohjelman, joka ratkaisee yhtälöitä puolestamme.
Ongelma:
Kolmion sivujen pituudet ovat [[$x$]], [[$2x$]] ja [[$2x$]] eli kolmion kaksi pidempää sivua ovat kaksi kertaa niin pitkiä kuin lyhyt sivu. Tiedetään, että kolmion piiri on [[$25 \ cm$]] ja halutaan tietää, kuinka pitkiä kolmion sivut ovat.
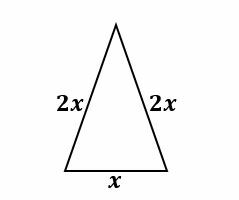
Tilanteesta saadaan helposti muodostettua yhtälö. Koska kolmion piiri saadaan laskemalla yhteen kolmion sivujen pituudet, niin yhtälö on [[$$x+2x+2x \ = \ 25 \ cm.$$]]
Nyt tuntemattoman muuttujan [[$x$]] paikalle voidaan kokeilla eri lukuja ja etsiä se muuttujan [[$x$]] arvo, joka toteuttaa yhtälön.
Muuttujan [[$x$]] oikea arvo on [[$5 \ cm$]], joten kolmion sivujen pituudet ovat [[$5 \ cm$]], [[$10 \ cm$]] ja [[$10 \ cm$]].
Mutta:
Ratkaisun etsiminen kokeilemalla eri vaihtoehtoja voi olla työlästä, etenkin jos muuttujan [[$x$]] ratkaisu on suuri luku.
Kun jotakin asiaa pitää mekaanisesti toistaa monta kertaa, kuten tässä tapauksessa, niin on kätevää antaa tietokoneen hoitaa likainen työ. Tähän tarvitaan ohjelmointia.
Alla on ohjelma, joka kokeilee muuttujan [[$x$]] arvoja 1 senttimetrin välein alkaen annetusta alkuarvosta. Ohjelma lopettaa kokeilun, kun oikea arvo löytyy tai kunnes [[$x$]] on niin suuri, ettei ratkaisua voi löytyä. (Paina Run.)
Tämän sivun alasivuilta löytyvien tehtävien avulla sinunkin pitäisi pystyä luomaan ohjelma, joka ratkaisee vastaavia ongelmia puolestasi.
Ongelma:
Kolmion sivujen pituudet ovat [[$x$]], [[$2x$]] ja [[$2x$]] eli kolmion kaksi pidempää sivua ovat kaksi kertaa niin pitkiä kuin lyhyt sivu. Tiedetään, että kolmion piiri on [[$25 \ cm$]] ja halutaan tietää, kuinka pitkiä kolmion sivut ovat.

Tilanteesta saadaan helposti muodostettua yhtälö. Koska kolmion piiri saadaan laskemalla yhteen kolmion sivujen pituudet, niin yhtälö on [[$$x+2x+2x \ = \ 25 \ cm.$$]]
Nyt tuntemattoman muuttujan [[$x$]] paikalle voidaan kokeilla eri lukuja ja etsiä se muuttujan [[$x$]] arvo, joka toteuttaa yhtälön.
| [[$x$]] | [[$x+2x+2x$]] | Piiri |
|---|---|---|
| [[$ 1 $]] | [[$1+2\cdot 1 + 2\cdot 1=5$]] | [[$5 \ cm$]] |
| [[$2 $]] | [[$2+2\cdot 2 + 2\cdot 2=10$]] | [[$10 \ cm$]] |
| [[$ 3 $]] | [[$3+2\cdot 3 + 2\cdot 3=15$]] | [[$15 \ cm$]] |
| [[$ 4 $]] | [[$4+2\cdot 4 + 2\cdot 4=20$]] | [[$20 \ cm$]] |
| [[$ 5 $]] | [[$5+2\cdot 5 + 2\cdot 5=25$]] | [[$25 \ cm$]] |
Muuttujan [[$x$]] oikea arvo on [[$5 \ cm$]], joten kolmion sivujen pituudet ovat [[$5 \ cm$]], [[$10 \ cm$]] ja [[$10 \ cm$]].
Mutta:
Ratkaisun etsiminen kokeilemalla eri vaihtoehtoja voi olla työlästä, etenkin jos muuttujan [[$x$]] ratkaisu on suuri luku.
Kun jotakin asiaa pitää mekaanisesti toistaa monta kertaa, kuten tässä tapauksessa, niin on kätevää antaa tietokoneen hoitaa likainen työ. Tähän tarvitaan ohjelmointia.
Alla on ohjelma, joka kokeilee muuttujan [[$x$]] arvoja 1 senttimetrin välein alkaen annetusta alkuarvosta. Ohjelma lopettaa kokeilun, kun oikea arvo löytyy tai kunnes [[$x$]] on niin suuri, ettei ratkaisua voi löytyä. (Paina Run.)
Tämän sivun alasivuilta löytyvien tehtävien avulla sinunkin pitäisi pystyä luomaan ohjelma, joka ratkaisee vastaavia ongelmia puolestasi.