7 Muuttujat
Mihin matematiikassa tarvitaan kirjaimia?
- Kirjaimien avulla kirjoitettua laskemisohjetta kutsutaan usein laskukaavaksi tai muuttujalausekkeeksi
- Laskukaavalla on sanallista selitystä helpompi ilmaista tarkasti, mitä lasketaan ja miten.
- Laskukaavoja tarvitaan melkein kaikissa fysiikan laskuissa 8. luokalta alkaen
- Kaavoja ja muuttujalausekkeita tarvitaan 8. ja 9. luokan geometriassa
- Taulukkolaskenta ja ohjelmointi edellyttävät laskutoimituksia kaavojen avulla
- Kaavoja tai muuttujalausekkeita tarvitaan kemiassa, taloustieteessä, biologiassa, metsätaloudessa, kaikenlaisessa suunnittelussa ja niin teollisen valmistuksen kuin käsityövalmistuksen tukena.
- Lisäksi kirjaimien käyttäminen lausekkeissa hiljalleen vapauttaa ajattelua ja parantaa oppimista!
Muuttujat lausekkeessa
Muuttuja
- Luku, joka voi olla tuntematon
- Voi saada eri arvoja
- Merkitään kirjaimella, usein x
- Lausekkeissa on usein kirjaimia
Ⓔ lukujen x ja 11 summa: x + 11 - Jos lausekkeessa on useita muuttujia, jokaisella on eri kirjain
Ⓔ m + 3n - Muuttujan vastakohta on vakio
- Vakiot ovat numeroita ja lukuja
Ⓔ 6 ja 32,5 ovat vakioita
Muuttujalausekkeen sieventäminen
- Kirjainta edeltävä kertomerkki jätetään pois
Ⓔ 3 ⋅ c = 3c
Ⓔ −12 ⋅ x = −12x - Kirjainta edeltävä ykkönen jätetään pois
Ⓔ 1c = c
Ⓔ −1 ⋅ x = −x - Myös sulkulauseketta edeltävä kertomerkki on turha
Ⓔ 2 ⋅ (1⋅ x − 1) = 2(x − 1)
Termi
- Lausekkeen "jäseniä" kutsutaan termeiksi.
- Lauseke on termienä summa
Ⓔ lausekkeessa 7a −13x + 2 on kolme termiä,- muuttujatermit 7a ja −13x
- vakiotermi 2
- Huom: Termien summa sievenee näin:
7a + (−13x) + 2 = 7a −13x + 2
- Muuttujatermiin kuuluu kerroinosa ja kirjainosa
Ⓔ termin −13x
- kerroinosa on −13
- muuttujaosa on x
Termien yhdistäminen
- Termien yhdistäminen on osa muuttujalausekkeen sieventämistä
- Jos termit ovat keskenään samanmuotoiset, ne yhdistetään
- Termit ovat keskenään samanmuotoiset, jos niillä on sama kirjainosa
Ⓔ 6x + 2x = 8x
Ⓔ 7ab − ab = 6ab - Vakiot ovat keskenään samanmuotoisia, koska niillä ei ole kirjainosaa
Ⓔ 7 + 3 = 10

Kuva: Sieventäminen vaiheittain on kuin etenemistä sarjakuvassa. Lauseke kirjoitetaan uudestaan kunnes se on riittävän sievä. Muuttujalausekkeessa samanmuotoiset termit yhdistetään.
Lausekkeeseen sijoittaminen
- Näin muuttujalausekkeita hyödynnetään!
- Jos muuttujan arvo tiedetään, lausekkeen arvo voidaan laskea sijoittamalla muuttujan arvo lausekkeeseen
Ⓔ jos meillä on lauseke x + 11 ja tiedämme, että x = 3, niin
x + 11 = 3 + 11 = 14 - Kun lasket muuttujalausekkeen arvoa, tärkein välivaihe tehtävässäsi on sijoittaminen. Sitä ei saa ohittaa.
Alla oleva sarjakuva korostaa asiaa.
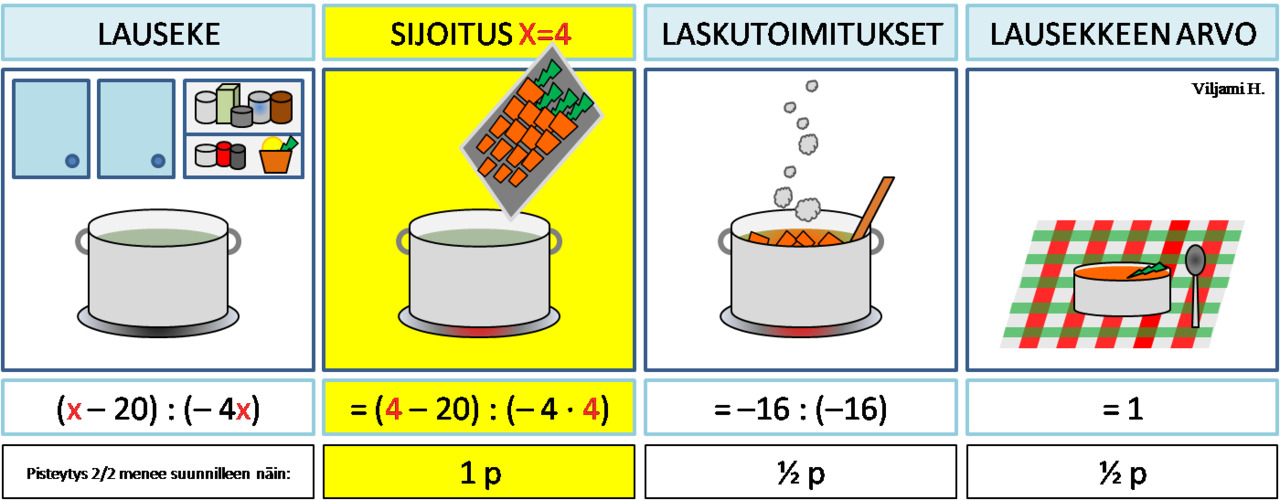
Kuva: Muuttujalausekkeen arvo voidaan laskea, mikäli muuttujan arvo tunnetaan. Muuttujan arvo sijoitetaan lausekkeeseen. Sitten lasketaan lausekkeen laskutoimitukset laskujärjestyssopimuksen mukaisesti. Vastauksena saadaan lausekkeelle lukuarvo.