Mekaniikan ratkaisuperiaatteet

Oheisessa taulukossa on koottuna keskeiset mekaniikan periaatteet, jotka kurssilla on käyty läpi. Vaikka kaikki periaatteet pitävät aina paikkansa, sopivan periaatteen valinta riippuu tilanteessa ratkaistavista suureista ja tunnetuista alkuarvoista. Usein yksi kolmesta on tilanteen ratkaisemiseksi hyödytön, ja kahdesta käyttökelpoisesta tavasta ongelma on toisella ratkaistavissa huomattavasti helpommin.

Keskeiset periaatteet
	Dynamiikan peruslaki	Energiaperiaate	Impulssiperiaate
Yleinen muoto	[[$\Sigma \overline{F}=m\overline{a}$]]	[[$E_1\pm W=E_2$]]	[[$\Delta \overline{p}=\overline{I}=\overline{F}\Delta t$]]
Periaatteen erikoistapaus	Voimien summa nolla: kappale on levossa tai liikkuu vakionopeudella [[$\Sigma \overline {F}=0$]]	Vain konservatiivisia voimia: mekaaninen energia säilyy [[$E_{\text{K}1}+E_{\text{P}1} \\=E_{\text{K}2}+E_{\text{P}2}$]]	Systeemiin ei vaikuta ulkoisia voimia: liikemäärä ei muutu [[$\overline{p}_1=\overline{p}_2$]]
Tyypillisiä piirteitä tilanteissa, joihin periaatetta kannattaa soveltaa	Käsitellään kiihtyvyyksiä ja/tai aikoja	Vertaillaan alku- ja lopputilannetta, niiden välinen aika ei ole oleellinen	Lyhytkestoinen vuorovaikutus (kuten törmäys, lyönti tai heitto)
	Kokonaisvoima on vakio (tasaisesti kiihtyvä liike)	Paikan suhteen muuttuva voima [[$(x,F)$]]-kuvaaja	Ajan suhteen muuttuva voima [[$(t,F)$]]-kuvaaja

Tehtävien tilanne voi sisältää myös useita ratkaisumalleja. Tilanne voi koostua kahden kappaleen vuorovaikutuksesta, jolloin sovelletaan liikemäärän säilymislakia, minkä jälkeen tutkitaan vain toisen kappaleen liikettä esimerkiksi energiaperiaatteen kautta.

Pystysuoran heittoliikkeen mallintaminen

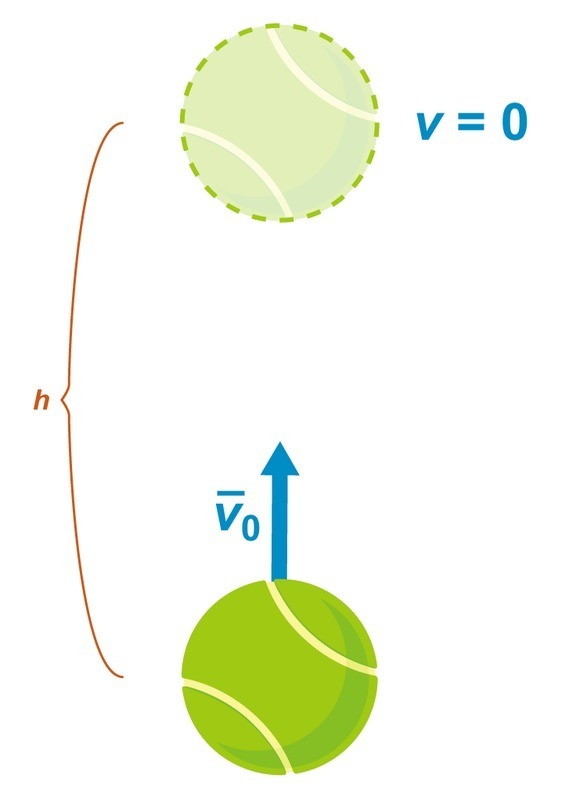Pesäpallo heitetään suoraan ylöspäin lähtönopeudella v. Ratkaistaan pallon nousukorkeus h ja nousuun kuluva aika t.

Nousukorkeuden ratkaiseminen mekaanisen energian avulla

Pallon mekaaninen energia säilyy. Sillä on alussa liike-energiaa ja lakipisteessä potentiaalienergiaa. Nousukorkeus saadaan selville muodostamalla energiaperiaateyhtälö ja ratkaisemalla se:

[[$ \begin{align*} E_\text {K alku}&=E_\text {P loppu} & \\ \,\\ \quad \dfrac{1}{2}m{v_0}^2&=mgh &||:m \\ \,\\ \dfrac{{v_0}^2}{2}&=gh &||:g \\ \,\\ h&=\dfrac{{v_0}^2}{2g} & \\ \end{align*} $]]

Nousuajan ratkaiseminen ei ole energian säilymisen kautta mahdollista, sillä aika ei esiinny energian lausekkeissa.

Nousukorkeuden ja nousuajan ratkaiseminen Newtonin 2. lain ja kinematiikan avulla

Ainoa palloon kohdistuva voima on paino, joten Newtonin 2. lain mukaan sen liikeyhtälö on

[[$ \begin {align*} F&=ma &(F=G=mg) \\ \,\\ \quad mg&=ma &||:m \\ \,\\ a&=g \\ \end{align*} $]]

Tasaisesti kiihtyvän liikkeen loppunopeus lasketaan kaavalla [[$ v=v_0+at $]]. Loppunopeus on nolla ja kiihtyvyys g on negatiivinen. Ratkaistaan nousuaika.

[[$\begin{align*} 0&=v_0-gt \\ \,\\ \quad gt&=v_0 \\ \,\\ t&=\dfrac{v_0}{g} \\ \end{align*} $]]

Pallon paikka (eli korkeus h) voidaan laskea tasaisesti kiihtyvässä liikkeessä kaavalla

[[$ \begin{align*} \quad h&=v_0 t+\dfrac{1}{2}at^2\\ \, \\ h&=v_0t-\dfrac{1}{2}gt^2 \end{align*} $]].

Sijoitetaan kaavaan ratkaistu nousuaika.

[[$ \begin{align*} \quad h&=v_0\dfrac{v_0}{g}-\dfrac{1}{2}g \left( {\dfrac{v_0}{g}} \right)^2\\ \, \\ h&=\dfrac{{v_0}^2}{g}-\dfrac{{v_0}^2}{2g}\\ \, \\ h&=\dfrac{{v_0}^2}{2g} \end{align*} $]]

Saatu nousukorkeuden h lauseke on sama kuin energian säilymislaskussa.

Nousuajan ja nousukorkeuden ratkaiseminen impulssiperiaatteen avulla

Impulssiperiaatteen mukaan painovoima antaa kappaleelle impulssin, joka muuttaa pallon liikemäärää. Otetaan huomioon liikkeen suunta, jolloin voima ja liikemäärän muutos ovat negatiivisia.

[[$ \quad \begin {align*} F\Delta t&= \Delta p & \\ \,\\ -Gt&=p_1-p_0 & \\ \,\\ -mgt&=0-mv_0 &||:(-mg) \\ \,\\ t&=\dfrac{v_0}{g} & \\ \end{align*} $]]

Saatu nousuajan lauseke on sama kuin Newtonin 2. lain perusteella saatu. Nousukorkeus on mahdollista ratkaista tasaisesti kiihtyvän liikkeen yhtälöstä, kuten Newtonin 2. lain tapauksessa.