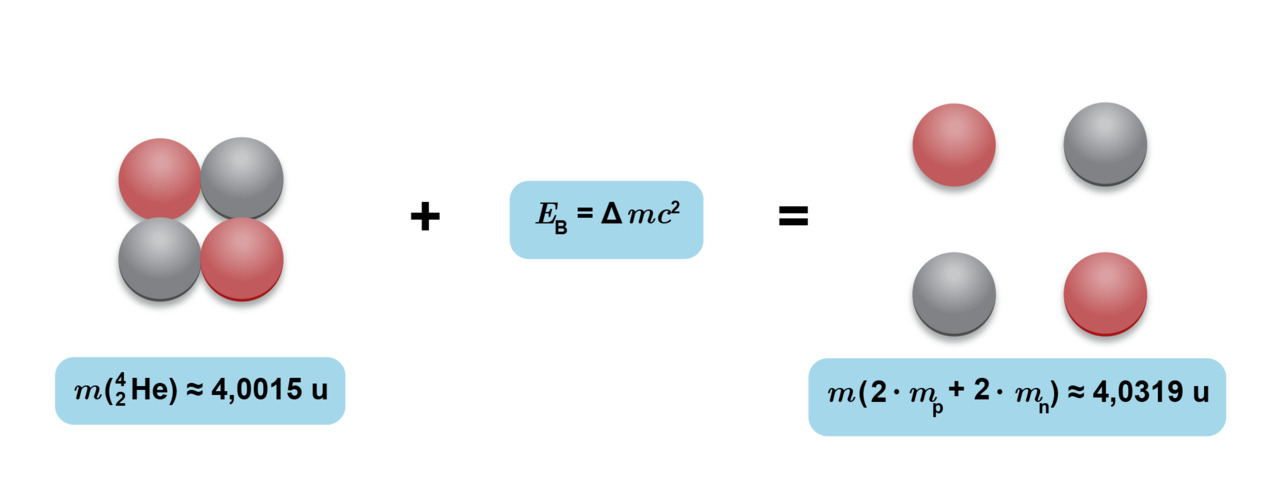Atomiydin ja alkuaineen ominaisuudet

Edellisessä luvussa tutkittiin atomin elektroneja ja niiden energiatiloja. Energiatilat ovat erimuotoisia elektronin sijainnin todennäköisyysjakaumia atomiytimen ympärillä. Atomin kokona voidaan pitää aluetta, jonka sisällä elektronit suurella todennäköisyydellä ovat. Atomin ydin on tähän verrattuna todella pieni: ytimen halkaisija on vain n. 1/10 000 itse atomin halkaisijasta. Suurin osa atomista on siis ei mitään, tyhjää. Atomiydin koostuu positiivisesti varautuneista protoneista ja varauksettomista neutroneista. Näitä hiukkasia, joista atomiytimet koostuvat, kutsutaan nukleoneiksi.

Atomin järjestysluku Z kertoo atomissa olevien protonien lukumäärän. Koska atomi on sähkövaraukseltaan neutraali, siinä on yhtä monta elektronia ja protonia. Atomin elektronirakenne määrittää aineen kemialliset ominaisuudet. Atomin järjestysluku on sama kuin protonien lukumäärä atomissa. Jokaisella alkuaineella on sille ominainen protonien lukumäärä. Esimerkiksi hiilen järjestysluku on 6, joten jokaisessa hiiliatomissa on 6 protonia.

Kaukana ytimestä olevien elektronien lisääminen ja poistaminen on suhteellisen helppoa verrattuna ytimen hajottamiseen. Elektronien lisääminen tai poistaminen atomista muuttaa sen negatiiviseksi tai positiiviseksi ioniksi. Tämä ei kuitenkaan muuta alkuainetta toiseksi eikä vaihda sen järjestyslukua.

Atomin massaluku A kertoo protonien (Z) ja neutronien (N) yhteenlasketun lukumäärän atomissa, eli nukleonien lukumäärän: A=Z+N. On havaittu, että saman alkuaineen atomeilla voi olla eri massa. Tietyn alkuaineen atomilla voi olla eri määrä neutroneja. Tällöin puhutaan saman alkuaineen eri isotoopeista. Tietyn alkuaineen isotoopeilla on sama järjestysluku ja sama määrä elektroneja, joten ne ovat sähköisiltä ja kemiallisilta ominaisuuksiltaan samanlaisia. Tästä syystä isotooppeja ei voida erottaa toisistaan kemiallisin menetelmin, jotka perustuvat vain atomien elektronikuorten rakenteeseen. Erotteluun voidaan käyttää esimerkiksi oppikirjassa Resonanssi 7 esiteltyä massaspektrometria.

Alla olevassa kuvassa on kolme vedyn isotooppia, protium, deuterium ja tritium. Huomaa isotooppien merkintätapa. H on vedyn kemiallinen tunnus. Merkinnän vasemmassa alanurkassa on vedyn järjestysluku. Merkinnän vasemmassa ylänurkassa on vedyn isotoopin massaluku, eli protonien ja neutronien kokonaismäärä.

Nykyään tunnetaan 118 eri alkuainetta ja runsaat 3 000 isotooppia. Puhuttaessa tietystä alkuaineesta on siis täsmennettävä, mitä sen isotoopeista määritetään. Yleensä riittää vain massaluvun ilmoittaminen, koska järjestysluku nähdään alkuaineen kemiallisesta merkistä. Esimerkiksi merkintä U-230 tarkoittaa uraanin isotooppia, jonka massaluku on 230. Taulukkokirjasta nähdään uraanin järjestysluku 92, joten isotoopissa U-230 on 92 protonia ja 230-92=138 neutronia.

Samaa alkuainetta voi esiintyä luonnossa eri isotooppeina. Tällöin puhutaan suhteellisesta runsaudesta. Se kertoo, kuinka suuri osa aineesta on kutakin isotooppia. Esimerkiksi hiili esiintyy luonnossa kahtena vakaana isotooppina, joita ovat C-12 ja C-13. C-12 on huomattavasti yleisempi. Sen suhteellinen runsaus on noin 98,9 %, kun C-13-isotoopin suhteellinen runsaus on noin 1,1 %.

Isotoopit voidaan esittää isotooppikarttana, taulukkona, jossa vaakarivillä on neutronien ja pystysarakkeessa protonien lukumäärä (järjestysluku). Tietyn alkuaineen isotoopit ovat siten kaikki samassa sarakkeessa. Alla on linkki tällaiseen isotooppikarttaan. Kartassa on runsaasti tietoa isotooppien ominaisuuksista, joista osaan tutustutaan tämän opintojakson aikana.

Isotooppikartta (IAEA)

Atomiytimen rakenne

Atomiydin koostuu nukleoneista, eli positiivisesti varautuneista protoneista ja varauksettomista neutroneista. Protonit ja neutronit ovat massaltaan lähes yhtä suuret, neutroni vain hieman raskaampi. Näiden hiukkasten ei pitäisi voida muodostaa koossapysyvää rakennetta, sillä sähköisen vuorovaikutuksen takia positiivisesti varautuneet protonit hylkivät toisiaan. Ytimen koossapysymisen selittäminen edellyttää protonien ja neutronien sisäisen rakenteen tuntemista. On havaittu, että molemmat koostuvat kvarkeista. Kvarkit ovat alkeishiukkasia, eli ne eivät nykykäsityksen mukaan koostu enää pienemmistä osista. Protonissa on kaksi u-kvarkkia ja yksi d-kvarkki. Neutronin kvarkkirakenne on päinvastainen: kaksi d-kvarkkia ja yksi u-kvarkki. Eri kvarkkeja tarkastellaan lähemmin luvussa 5.1 Standardimalli.

Kvarkkien välillä on vahva vuorovaikutus, jolla on merkitystä vain hyvin lyhyillä etäisyyksillä. Vahva vuorovaikutus sitoo kvarkit toisiinsa erittäin pysyviksi kahden tai kolmen kvarkin kokonaisuuksiksi. Protoni ja neutroni ovat kolmen kvarkin muodostamia hiukkasia. Sen lisäksi, että vahva vuorovaikutus liittää yksittäiset kvarkit nukleoneiksi, se vaikuttaa jossain määrin myös vierekkäisten nukleonien kvarkkien välillä. Tästä syntyy nukleonien välille hylkivä voima niiden ollessa todella lähellä toisiaan ja puoleensavetävä voima niiden ollessa n. yhden femtometrin etäisyydellä toisistaan. Kauemmas mentäessä puoleensavetävä voima pienenee nopeasti. Tietyllä etäisyydellä vahvan vuorovaikutuksen aikaansaama vetovoima kumoaa sähköisen vuorovaikutuksen aiheuttaman hylkimisen, ja nukleonit sitoutuvat toisiinsa muodostaen atomiytimiä. Koska vahva vuorovaikutus kuitenkin heikkenee nopeammin kuin sähkömagneettinen vuorovaikutus etäisyyden kasvaessa, se ei pidä koossa miten suurta määrää tahansa nukleoneja. Suurimmissa vakaissa atomiytimissä on 244 nukleonia. Ytimissä on yleensä enemmän neutroneja kuin protoneja, koska neutronien välillä ei ole sähköistä poistovoimaa, ja vahvan vuorovaikutuksen on helpompi pitää ne yhdessä. Kuvassa on esitetty kahden protonin väliset voimat etäisyyden suhteen.

Atomimassa

Makroskooppisen kappaleen massa on suoraan verrannollinen kappaleen muodostavien atomien tai molekyylien lukumäärään N. Suurin osa atomin massasta on sen ytimessä, sillä protonit ja neutronit ovat n. 1 800 kertaa raskaampia kuin elektroni. Koska protoneilla ja neutroneilla on likimain sama massa, atomin massa on suunnilleen niiden yhteismäärä (massaluku) kerrottuna yksittäisen protonin tai neutronin massalla. Tätä ajatusta käyttäen on määritelty atomimassayksikkö u siten, että hiilen C-12-isotoopin massaksi on määritelty tasan 12 u:

[[$ \qquad m(^{12}\text{C})=12 \ \text{u} $]]

Hiili-12-isotoopin massasta saadaan yhden atomimassan suuruus. Esimerkiksi vedyn isotoopin H-1 massa atomimassayksiköissä on n. 1,0078 u. Atomin massa atomimassayksiköissä on aina likimäärin sama kuin atomin massaluku, ja useissa tilanteissa tämä tarkkuus riittää. Ero johtuu mm. elektronien massasta ja protonin ja neutronin massojen pienestä erosta. Molekyylien atomimassa on molekyylin muodostavien atomien atomimassojen summa.

Kilogrammoissa atomimassayksikkö eli dalton on [[$1\text{ u}=1{,}6605402\cdot 10^{-27}\text{ kg}$]]. Atomimassayksikkö on kätevä juuri siksi, että atomiydinten massat ovat hyvin pieniä.

Huomaa, että taulukkokirjan kemian osuudessa esitetään keskimääräiset atomimassat eri alkuaineille luonnossa esiintyvien isotooppien runsauden mukaan. Fysiikan osuudessa on isotooppitaulukko, jossa on eri isotooppien atomimassat ja niiden suhteelliset osuudet.

Massavaje ja sidosenergia

Kokeellisesti voidaan havaita, että heliumytimen massa on n. 0,8 % pienempi kuin ytimen muodostavien nukleonien massojen summa. Tämä voidaan selittää tulkitsemalla massa yhdeksi energiamuodoksi. Heliumytimen hajottamiseen vaadittu energia sitoutuu vapaiden nukleonien massoihin. Toisin päin voidaan ajatella, että kun kahdesta protonista ja kahdesta neutronista syntyy heliumatomi, vapautuva energia ilmenee massan vähenemisenä.

Ytimen hajottamiseen vaadittua energiaa kutsutaan sidosenergiaksi [[$ E_\text{B} $]]. Sama energia vapautuu ytimen muodostuessa rakenneosistaan. Rakenneosien yhteismassan ja ehjän ytimen massojen välistä eroa kutsutaan massavajeeksi [[$\Delta m$]]. Massavajeen ja sidosenergian yhteyttä kuvaa Albert Einsteinin esittämä kaava massan ja energian vastaavuudesta: [[$E=mc^2$]], missä [[$c$]] on valon nopeus.

Massavaje, sidosenergia ja niiden yhteys

Massavaje [[$\Delta m$]]: ytimen rakenneosasten yhteismassan ja ehjän ytimen massan ero.

[[$ \qquad \begin{align} \Delta m&=Z\cdot m_\text{p}+N\cdot m_\text{n} - m_\text{ydin} \\ \, \\ &=Z\cdot m_\text{p}+N\cdot m_\text{n} - \left(m_\text{atomi}-Z\cdot m_\text{e}\right) \end{align} $]]

Sidosenergia [[$E_\text{B}$]]: ytimen hajottamiseen vaadittu tai ytimen muodostuessa vapautuva energia.

Massan ja energian vastaavuus: [[$E=mc^2$]], eli [[$E_\text{B}=\Delta mc^2$]].

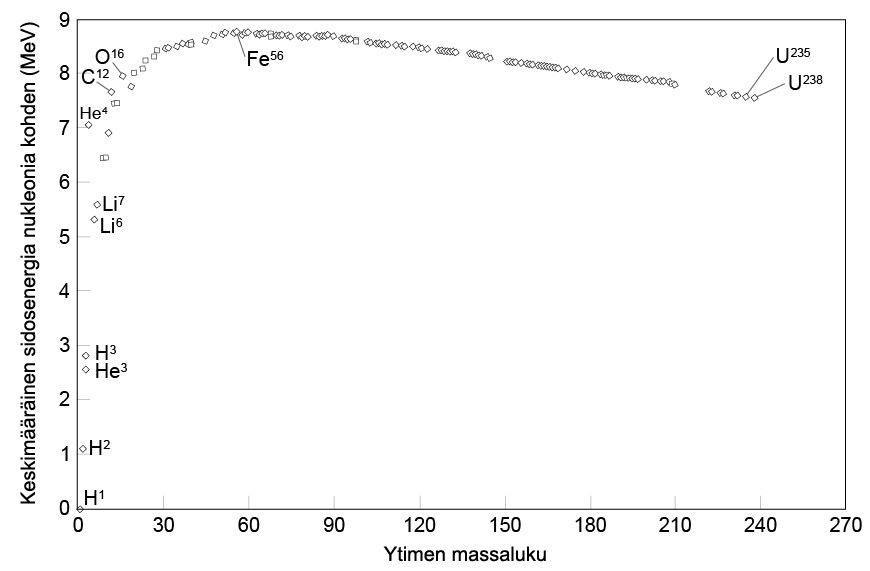
Sidosenergian määrä kasvaa, kun aineen massaluku A kasvaa, koska atomiytimessä ytimen rakenneosien välisten sidosten määrä kasvaa. Järkevä tapa verrata eri atomiydinten sidosenergioita on jakaa sidosenergia massaluvulla, eli tarkastella sidosenergiaa nukleonia kohden. Tämä tarkoittaa keskimääräistä energiamäärää, joka atomiytimeen pitäisi tuoda, jotta sieltä saataisiin irrotettua yksi nukleoni. Tätä energiamäärää kutsutaan sidososuudeksi.

Yllä olevassa kuvassa esitetään sidososuus massaluvun funktiona. Huomataan, että sidososuus kasvaa, kunnes suurin sidososuus (noin 8,7 MeV) saavutetaan massaluvuilla, jotka ovat 60 molemmin puolin. Suurimmat sidosenergiat ovat raudan ja nikkelin isotoopeilla. Tätä suuremmilla massaluvuilla sidososuus lähtee hitaasti pienenemään. Raskailla ja erittäin kevyillä ytimillä nukleonit ovat löyhemmin sitoutuneita toisiinsa kuin keskiraskailla. Tästä seuraa, että energiaa vapautuu kahden kevyen ytimen yhdistyessä raskaammaksi ytimeksi aina rautaan asti. Ydinten yhdistymistä kutsutaan fuusioksi. Vastaavasti rautaa raskaammilla alkuaineilla energiaa vapautuu, kun niitä hajotetaan kevyemmiksi ytimiksi. Ytimen hajoamista kutsutaan fissioksi.

Ytimen sidososuus

Sidososuus ilmaisee sidosenergian määrän yhtä nukleonia kohden:

[[$ \qquad b=\dfrac{E_B}{A} $]]

Atomimassayksikkö ja energia

Atomimassayksikkö on kilogrammoina [[$ 1 \text{ u}\approx 1{,}6605 \cdot 10^{-27} \text{ kg} $]]. Käyttämällä Einsteinin kaavaa massan ja energian vastaavuudesta [[$ E=mc^2 $]] voidaan laskea yhtä atomimassayksikköä vastaavan energian suuruus:

[[$ \qquad\begin{align}E&=mc^2 \\ \, \\ &=1{,}6605\cdot10^{-27} \text{ kg} \cdot (2{,}9979 \cdot 10^8 \text{ m/s})^2 \\ \, \\ &=1{,}4923 \dots \cdot 10^{-10} \text{ J}\\ \, \\ & \approx931{,}49 \text{ MeV} \end{align} $]]

Siis [[$ 1 \text{ u}\approx 931{,}49 \text{ MeV/c}^2 $]]. Tämä on usein kätevä yksikkö laskuissa.