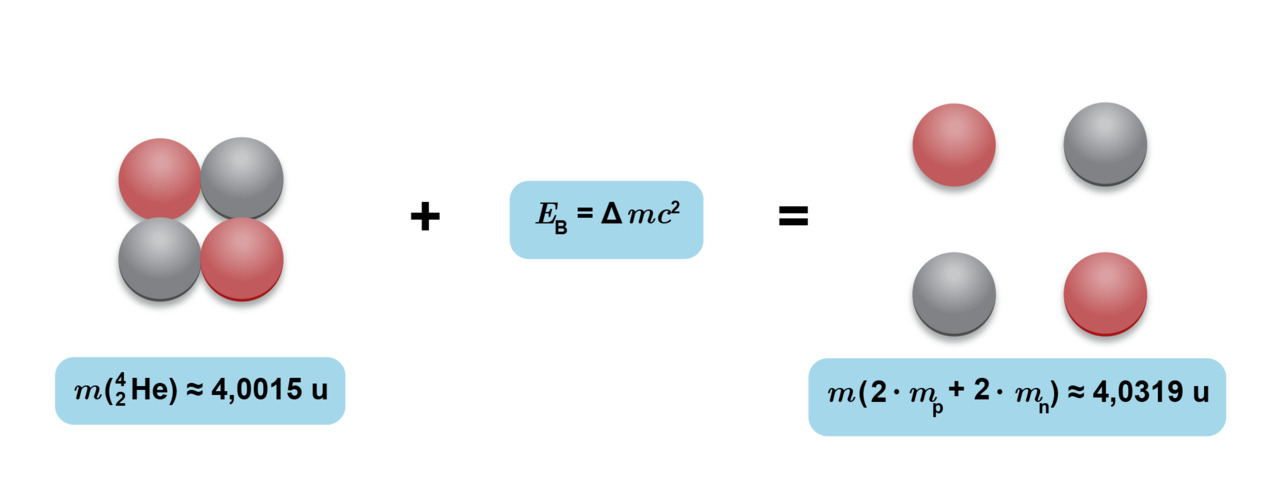Kokeellisesti voidaan havaita, että heliumytimen massa on n. 0,8 % pienempi kuin ytimen muodostavien nukleonien massojen summa. Tämä voidaan selittää tulkitsemalla massa yhdeksi energiamuodoksi. Heliumytimen hajottamiseen vaadittu energia sitoutuu vapaiden nukleonien massoihin. Toisin päin voidaan ajatella, että kun kahdesta protonista ja kahdesta neutronista syntyy heliumatomi, vapautuva energia ilmenee massan vähenemisenä.

Ytimen hajottamiseen vaadittua energiaa kutsutaan sidosenergiaksi [[$ E_\text{B} $]]​. Sama energia vapautuu ytimen muodostuessa rakenneosistaan. Rakenneosien yhteismassan ja ehjän ytimen massojen välistä eroa kutsutaan massavajeeksi [[$\Delta m$]]. Massavajeen ja sidosenergian yhteyttä kuvaa Albert Einsteinin esittämä kaava massan ja energian vastaavuudesta: [[$E=mc^2$]], missä [[$c$]] on valon nopeus.

Sidosenergian määrä kasvaa, kun aineen massaluku A kasvaa, koska atomiytimessä ytimen rakenneosien välisten sidosten määrä kasvaa. Järkevä tapa verrata eri atomiydinten sidosenergioita on jakaa sidosenergia massaluvulla, eli tarkastella sidosenergiaa nukleonia kohden. Tämä tarkoittaa keskimääräistä energiamäärää, joka atomiytimeen pitäisi tuoda, jotta sieltä saataisiin irrotettua yksi nukleoni. Tätä energiamäärää kutsutaan sidososuudeksi.

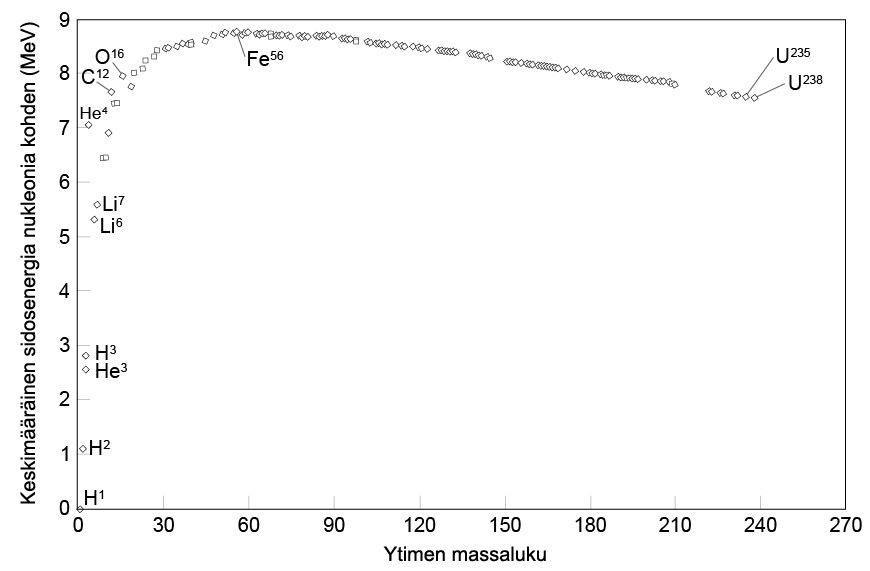
Yllä olevassa kuvassa esitetään sidososuus massaluvun funktiona. Huomataan, että sidososuus kasvaa, kunnes suurin sidososuus (noin 8,7 MeV) saavutetaan massaluvuilla, jotka ovat 60 molemmin puolin. Suurimmat sidosenergiat ovat raudan ja nikkelin isotoopeilla. Tätä suuremmilla massaluvuilla sidososuus lähtee hitaasti pienenemään. Raskailla ja erittäin kevyillä ytimillä nukleonit ovat löyhemmin sitoutuneita toisiinsa kuin keskiraskailla. Tästä seuraa, että energiaa vapautuu kahden kevyen ytimen yhdistyessä raskaammaksi ytimeksi aina rautaan asti. Ydinten yhdistymistä kutsutaan fuusioksi. Vastaavasti rautaa raskaammilla alkuaineilla energiaa vapautuu, kun niitä hajotetaan kevyemmiksi ytimiksi. Ytimen hajoamista kutsutaan fissioksi.