Teoria
Pohjatunti
Koska naru on kevyt ja venymätön, jännitysvoimat ovat yhtä suuret 
Koska köysi ei veny, pulkkien kiihtyvyydet ovat samat 
Newtonin II lain mukaan pulkkien liikeyhtälöt ovat
Pulkka 1: eli
eli
Pulkka 2: eli
eli
y-akselin suunnassa Pulkka 1:
Pulkka 2:
Jännitysvoima on:
Kpl.12
Esim. Auton kokonaismassa 1310kg ja nopeus 85 km/h. Jarruttavan kokonaisvoiman tekemä työ on 183 kJ. Mikä on auton nopeus jarrutulsen jälkeen?








![v_l=\sqrt[]{\frac{2W+mv_a^2}{m}}=\sqrt[]{\frac{2\cdot\left(-183\cdot10^3J\right)+1310kg\cdot\left(\frac{85}{3{,}6}\ \frac{m}{s}\right)}{1310kg}}\approx16{,}6762\ \frac{m}{s}\approx60\ \frac{km}{h}](https://math-demo.abitti.fi/math.svg?latex=v_l%3D%5Csqrt%5B%5D%7B%5Cfrac%7B2W%2Bmv_a%5E2%7D%7Bm%7D%7D%3D%5Csqrt%5B%5D%7B%5Cfrac%7B2%5Ccdot%5Cleft(-183%5Ccdot10%5E3J%5Cright)%2B1310kg%5Ccdot%5Cleft(%5Cfrac%7B85%7D%7B3%7B%2C%7D6%7D%5C%20%5Cfrac%7Bm%7D%7Bs%7D%5Cright)%7D%7B1310kg%7D%7D%5Capprox16%7B%2C%7D6762%5C%20%5Cfrac%7Bm%7D%7Bs%7D%5Capprox60%5C%20%5Cfrac%7Bkm%7D%7Bh%7D)
Koska työn tekee jarruttava voima, on voima suunta vastakkainen etenemiseeen nähden, W<0.
Työn suuruus on yhtä suri kuin liike-energian muutos ei
Kpl.9
Kpl.8
Olkoon kuution tahkon pinta.alan A ja sivun pituus h.
x= Vedenpinnan alapuolela olevan sivun pituus
Vedenpinnan alapuolella olevan jääpalan tilavuus
Pinnan yläpuolella on tilavuudesta:
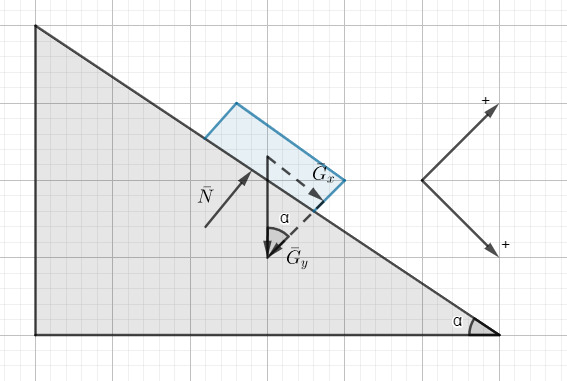
Kpl.6
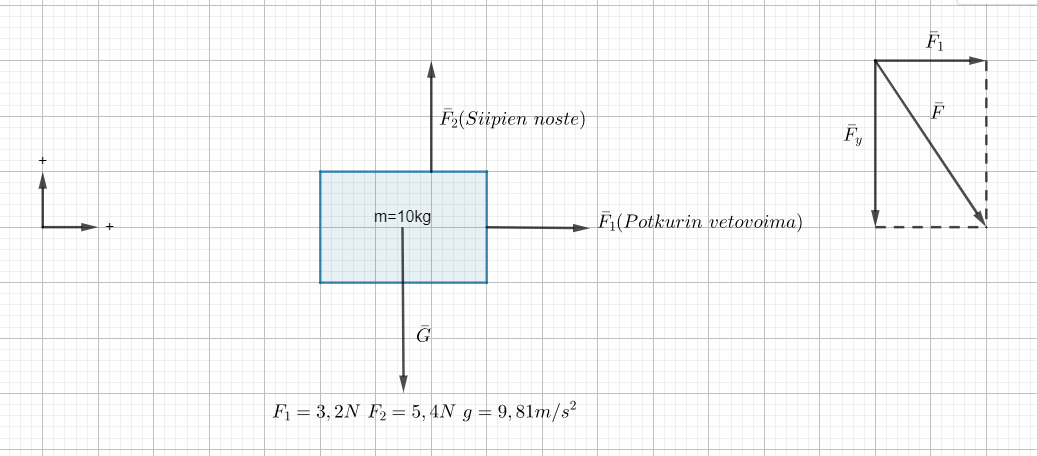
6. Voimien yhteisvaikutus



![F_{kok}=\sqrt[]{F_1^2+F_y^2}](https://math-demo.abitti.fi/math.svg?latex=F_%7Bkok%7D%3D%5Csqrt%5B%5D%7BF_1%5E2%2BF_y%5E2%7D)
![F_{kok}=\sqrt[]{F_1^2+\left(F_2-G\right)^2}=\sqrt[]{F_1^2+\left(F_2-mg\right)^2}](https://math-demo.abitti.fi/math.svg?latex=F_%7Bkok%7D%3D%5Csqrt%5B%5D%7BF_1%5E2%2B%5Cleft(F_2-G%5Cright)%5E2%7D%3D%5Csqrt%5B%5D%7BF_1%5E2%2B%5Cleft(F_2-mg%5Cright)%5E2%7D)
![F_{kok}=\sqrt[]{\left(3{,}2N\right)^2+\left(5{,}4N-10kg\cdot9{,}81\ \frac{m}{s^2}\right)^2}](https://math-demo.abitti.fi/math.svg?latex=F_%7Bkok%7D%3D%5Csqrt%5B%5D%7B%5Cleft(3%7B%2C%7D2N%5Cright)%5E2%2B%5Cleft(5%7B%2C%7D4N-10kg%5Ccdot9%7B%2C%7D81%5C%20%5Cfrac%7Bm%7D%7Bs%5E2%7D%5Cright)%5E2%7D)





Jos kappaleesee vaikuttaa useita voimia voimat voidaan yhdistää kokonaisoimaksi:
- Kohtisuorien voimien
ja
resultantin suuruus lasketaan pythagoraan lauseella:

Ja suuntakulma α yhtälöstä 
- Eri suuntiin osoittavien useiden voimien yhteisvaikutus saadaan piirtämällä voimavektorit peräläin ja yhdistämällä alkupiste viimeisen vektorin kärkeen:
- Jos resultantti on nolla vektori eli ) , kappale on levossa tai liikkuu vakionopeudella.
, kappale on levossa tai liikkuu vakionopeudella.
NII: 
Yhdistetään esnin voimat ja
ja  :
:
Vaikuttavat y-suunnassa, jote kokonaisvoima y-suunnassa on
Voidaan ajatella, että vaikuttavat voimat ovat  ja
ja 
Kiihtyvyys on kokonaisvoiman suuntaan
V: Lentokone laskeutuu 9,3 m/s² kiihtyvyydellä 88° vaakatsosta alaspäin.