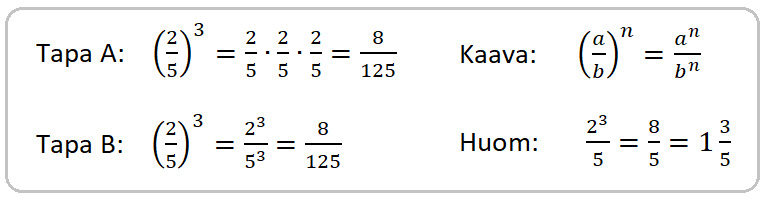Potenssimerkintä

• Muodostuu kantaluvusta ja exponentista
• Kantalukua kerrotaan itsellään niin monta kertaa kuin exponentti määrää
• Kaava: aⁿ = a ⋅ a ⋅ a ⋅ ... ⋅ a (tulontekijöinä n kappaletta a)
• Missä a on kantaluku ja n on exponentti.
  Ⓔ Merkitse ja laske potenssilauseke, jossa kantaluku on 5 ja exponentti on 3.
  Merkitse: 5³
  Laske: = 5 ⋅ 5 ⋅ 5 = 125

Luvun neliö

• On luvun toinen potenssi eli exponentti on kaksi
• Viittaa neliön pinta-alan laskukaavaan A=a²
• Viittaa samalla siihen, että pinta-alan käsite vaatii kaksi ulottuvuutta, x ja y.
  Ⓔ Laske luvun kuusi neliö eli korota luku kuusi toiseen potenssiin
  Vastaus: 6² = 6 ⋅ 6 = 36

Luvun kuutio

• On luvun kolmas potenssi eli exponentti on kolme
• Viittaa kuution tilavuuden laskukaavaan V=a³
• Viittaa samalla siihen, että tilavuuden hahmottaminen vaatii kolme ulottuvuutta, x, y ja z.
  Ⓔ Laske luvun kuusi kuutio eli korota luku kuusi kolmanteen potenssiin
  Vastaus: 6³ = 6 ⋅ 6 ⋅ 6 = 216

Negatiivinen kantaluku

• Vaatii sulkeet ympärilleen
• Muuten etumerkki ei ole osa potenssilauseketta
• Tulon merkkisääntöjen mukaan parillisilla exponenteilla potenssin arvo on positiivinen ja parittomilla negatiivinen.

Kantaluku 3	Potenssin arvo		Kantaluku −3	Potenssin arvo
31	= 3		(−3)1	= −3
32 = 3 ⋅ 3	= 9		(−3)2 = −3 ⋅ (−3)	= 9
33 = 3 ⋅ 3 ⋅ 3	= 27		(−3)3 = −3 ⋅ (−3) ⋅ (−3)	= −27
34 = 3 ⋅ 3 ⋅ 3 ⋅ 3	= 81		(−3)4 = −3 ⋅ (−3) ⋅ (−3) ⋅ (−3)	= 81

Huom: −3² = − 3 ⋅ 3 = −9

Kantalukuna murtoluku

• Vaatii sulkeet ympärilleen
• Muuten exponentti vaikuttaa vain osoittajaan tai nimittäjään
  Ⓔ Laske potenssi, kun kantaluku on 2/5 ja eksponentti on 3

• Huomaathan, että jakolasku voidaan aina tulkita murtolukuna.
  Ⓔ Siksi (2 : 5)³ = 2³ : 5³ = 8 : 125 = 8/125