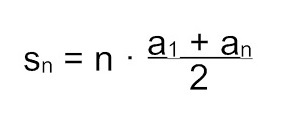4. Lukujonot ja summat
4.1 Lukujono
Lukujen muodostamia jono kutsutaan lukujonoiksi. Niiden avulla voidaan mallintaa esim. orgaanisen kemian hiilivetyjen rakenteita, itsekoottavien huonekalujen ruuvipakkausten sisältöä sekä säästämisen ja lainottamisen sisältämää matematiikkaa.
Lukujono voi sisältää tunnetun määrän lukuja, jolloin lukujono on äärellinen. Lukujonossa on siis viimeinen luku.
Lukujonon ollessa ääretön eli päättymätön, ei lukujono viimeistä lukua voida määrittää.
Esimerkkejä:
2, 4 , 6, 8 on äärellinen lukujono - sisältää neljä lukua.
1, 2, 3 , 4,... on ääretön lukujono eli päättymätön.
10, 20, 30,...,80, 90, 100 on äärellinen lukujono - sisältää kymmenen lukua.
------------------------------------------------------------------------------------------------------------------------------------------
Lukujonossa olevia lukuja kutsutaan lukujonon jäseniksi tai termeiksi. Termit on järjestetty niin, että jokaisen termin paikalla on merkitys. Siksi jokainen jäsen voidaan ilmaista järjestysnumeron avulla. Järjestysnumero ilmaistaan alaindeksillä, joka on positiivinen kokonaisluku. Numerointi alkaa aina numerosta yksi.
Yleisesti kaikki lukujonot voidaan kirjoittaa muotoon
a1, a2, a3, a4,...., ai → lukujonossa on siis jäseniä i kappaletta
Tällä tavalla lukujonojen tulkinta ja tarkastelu voidaan suorittaa koordinaatistosta, kun järjestysluvut sovitetaan positiiviselle x-akselille. Silloin lukujonot muodostaa koordinaatistoon kuvaajan, mikäli lukujono on säännönmukainen.
------------------------------------------------------------------------------------------------------------------------------------------
Lukujono voi muodostua tietyn säännön eli matemaattisen kaavan tai lausekkeen avulla. Sääntö voidaan kirjoittaa siis lausekkeena, jossa muuttuja on lukujonon jäsenen järjestysnumero. Tällöin lukujonon tarkastelu helpottuu ja voidaan tutkia myös lukujonon suurimpia termejä ja niiden arvoja.
Esim.
parillisten lukujen jono 2, 4, 6, 8,....voidaan esittää yleisesti muodossa an = 2n. Näin mikä tahansa lukujonon termi saadaan sijoittamalla haluttu numero n:n paikalle. a1221 = 2 · 1221 = 2442
parittomien lukujen jono 1, 3, 5, 7,...voidaan esittää vastaavasti muodossa an = 2n - 1.
------------------------------------------------------------------------------------------------------------------------------------------
Lukujono voi sisältää tunnetun määrän lukuja, jolloin lukujono on äärellinen. Lukujonossa on siis viimeinen luku.
Lukujonon ollessa ääretön eli päättymätön, ei lukujono viimeistä lukua voida määrittää.
Esimerkkejä:
2, 4 , 6, 8 on äärellinen lukujono - sisältää neljä lukua.
1, 2, 3 , 4,... on ääretön lukujono eli päättymätön.
10, 20, 30,...,80, 90, 100 on äärellinen lukujono - sisältää kymmenen lukua.
------------------------------------------------------------------------------------------------------------------------------------------
Lukujonossa olevia lukuja kutsutaan lukujonon jäseniksi tai termeiksi. Termit on järjestetty niin, että jokaisen termin paikalla on merkitys. Siksi jokainen jäsen voidaan ilmaista järjestysnumeron avulla. Järjestysnumero ilmaistaan alaindeksillä, joka on positiivinen kokonaisluku. Numerointi alkaa aina numerosta yksi.
Yleisesti kaikki lukujonot voidaan kirjoittaa muotoon
a1, a2, a3, a4,...., ai → lukujonossa on siis jäseniä i kappaletta
Tällä tavalla lukujonojen tulkinta ja tarkastelu voidaan suorittaa koordinaatistosta, kun järjestysluvut sovitetaan positiiviselle x-akselille. Silloin lukujonot muodostaa koordinaatistoon kuvaajan, mikäli lukujono on säännönmukainen.
------------------------------------------------------------------------------------------------------------------------------------------
Lukujono voi muodostua tietyn säännön eli matemaattisen kaavan tai lausekkeen avulla. Sääntö voidaan kirjoittaa siis lausekkeena, jossa muuttuja on lukujonon jäsenen järjestysnumero. Tällöin lukujonon tarkastelu helpottuu ja voidaan tutkia myös lukujonon suurimpia termejä ja niiden arvoja.
Esim.
parillisten lukujen jono 2, 4, 6, 8,....voidaan esittää yleisesti muodossa an = 2n. Näin mikä tahansa lukujonon termi saadaan sijoittamalla haluttu numero n:n paikalle. a1221 = 2 · 1221 = 2442
parittomien lukujen jono 1, 3, 5, 7,...voidaan esittää vastaavasti muodossa an = 2n - 1.
------------------------------------------------------------------------------------------------------------------------------------------
4.2. Rekursiivinen lukujono
Rekursiivisessa lukujonossa jäsenet muodostetaan käyttämällä apuna aiemmin muodostettua termejä. Tällainen lukujono koostuu kahdesta osasta: a) alkuarvosta ja b) rekursioyhtälöstä. Huomaa, että alkuarvoja voi olla useampi kuin yksi. Yhtälön avulla siis saadaan laskettua aina seuraava jäsen, kun yhtälöön sijoitetaan aiemmin laskettu, edellinen termi.
Esimerkki 1.
Muodosta rekursiivisen lukujonon 6 ensimmäistä jäsentä, kun tiedetään, että
a1 = 2 ja
an = 2 · an-1 - 1, kun n = 2, 3, 4,...
a1 = 2
a2 = 2 · 2 - 1 = 3
a3 = 2 · 3 - 1 = 5
a4 = 2 · 5 - 1 = 9
a5 = 2 · 9 - 1 = 17
a6 = 2 · 17 - 1 = 33
Esimerkki 2.
Fibonaccin lukujono on yksi kuuluisimpia lukujonoja. Se voidaan muodostaa seuraavin ehdoin:
a1 = 1, a2 = 1 ja an = an - 1 + an - 2
Muodosta Fibonaccin lukujonon 8 ensimmäistä termiä.
Esimerkki 1.
Muodosta rekursiivisen lukujonon 6 ensimmäistä jäsentä, kun tiedetään, että
a1 = 2 ja
an = 2 · an-1 - 1, kun n = 2, 3, 4,...
a1 = 2
a2 = 2 · 2 - 1 = 3
a3 = 2 · 3 - 1 = 5
a4 = 2 · 5 - 1 = 9
a5 = 2 · 9 - 1 = 17
a6 = 2 · 17 - 1 = 33
Esimerkki 2.
Fibonaccin lukujono on yksi kuuluisimpia lukujonoja. Se voidaan muodostaa seuraavin ehdoin:
a1 = 1, a2 = 1 ja an = an - 1 + an - 2
Muodosta Fibonaccin lukujonon 8 ensimmäistä termiä.
4.3. Aritmeettinen lukujono
Aritmeettisessa lukujonossa minkä tahansa kahden peräkkäisen termin erotus on aina sama. Tämä voidaan esittää termien avulla seuraavasti:
esimerkki 1.
1, 4, 7, 10, 13,... on aritmeettinen lukujono, koska kahden peräkkäisen termin erotus on aina 3.
100, 90, 80, 70, 60, 50,... on aritm. lukujono, kahden peräkkäisen termin erotus on -10.
------------------------------------------------------------------------------------------------------------------------------------------
Aritmeettisen lukujonon yleinen termi an eli n. jäsen muodostetaan valmiin ratkaisukaavan avulla. Ratkaisukaavan käyttö perustuu erotusluvun d eli differentin käyttöön.
esimerkki 2. Muodosta aritmeettisen lukujonon 1, 4, 7, 10, 13,... yleinen termi.
Peräkkäisten termien erotus on kolme → d = 3.
Ensimmäinen jäsen on 1.
Yleinen termi on siis muotoa
an
= 1 + (n - 1) · 3
= 1 + 3n - 3
= 3n - 2
------------------------------------------------------------------------------------------------------------------------------------------
an - an-1 = d
d = erotusluku eli differentti
esimerkki 1.
1, 4, 7, 10, 13,... on aritmeettinen lukujono, koska kahden peräkkäisen termin erotus on aina 3.
100, 90, 80, 70, 60, 50,... on aritm. lukujono, kahden peräkkäisen termin erotus on -10.
------------------------------------------------------------------------------------------------------------------------------------------
Aritmeettisen lukujonon yleinen termi an eli n. jäsen muodostetaan valmiin ratkaisukaavan avulla. Ratkaisukaavan käyttö perustuu erotusluvun d eli differentin käyttöön.
an = a1 + (n - 1) · d
Riittää siis tietää lukujonon ensimmäinen termi ja erotusluku d.esimerkki 2. Muodosta aritmeettisen lukujonon 1, 4, 7, 10, 13,... yleinen termi.
Peräkkäisten termien erotus on kolme → d = 3.
Ensimmäinen jäsen on 1.
Yleinen termi on siis muotoa
an
= 1 + (n - 1) · 3
= 1 + 3n - 3
= 3n - 2
------------------------------------------------------------------------------------------------------------------------------------------
4.4 Aritmeettinen summa
Laskettaessa yhteen tietty määrä peräkkäisiä aritmeettisen lukujonon jäseniä saadaan aritmeettisen lukujonon summa. Summaa merkitään lyhenteellä Sn, missä S tarkoittaa summaa ja alaindeksi n on summattavien termien määrä.
Kokonaisluvut 1, 2, 3,...ovat osa aritmeettista lukujonoa. Merkintä S5 tarkoittaa siis laskua
S5 =1 + 2 + 3 + 4 + 5 = 15.
Aritmeettinen summa saadaan valmiina ratkaisukaavan avulla.
------------------------------------------------------------------------------------------------------------------------------------------
Summamerkintänä voidaan käyttää myös kreikkalaista merkkiä Σ (sigma), joka tarkoittaa summaa. Lisäksi on tunnettava aritmeettisen lukujonon yleisen jäsenen lause.
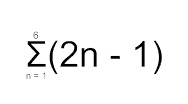
Tarkoittaa siis summaa kuudelle ensimmäiselle termille lukujonossa, jonka yleinen jäsen saadaan kaavalla an = 2n - 1. Lukunon ensimmäinen jäsen a1 = 1 ja kuudes jäsen a6 = 11.
Kaavaan sijoitettuna summaksi saadaan Σ = 6 · [(1 + 11) : 2] = 6 · 6 = 36
Summan voisi esittää myös muodossa 1 + 3 + 5 + 7 + 9 + 11 = 36
Summalausekkeet ovat käytännöllisiä silloin, kun yhteenlaskettavia on suuri määrä.
Esimerkki. Laske summa
------------------------------------------------------------------------------------------------------------------------------------------
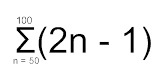
Kokonaisluvut 1, 2, 3,...ovat osa aritmeettista lukujonoa. Merkintä S5 tarkoittaa siis laskua
S5 =1 + 2 + 3 + 4 + 5 = 15.
Aritmeettinen summa saadaan valmiina ratkaisukaavan avulla.
- n on yhteenlaskettavien lukumäärä
- a1 on ensimmäinen yhteenlaskettava
- an on viimeinen yhteenlaskettava
------------------------------------------------------------------------------------------------------------------------------------------
Summamerkintänä voidaan käyttää myös kreikkalaista merkkiä Σ (sigma), joka tarkoittaa summaa. Lisäksi on tunnettava aritmeettisen lukujonon yleisen jäsenen lause.
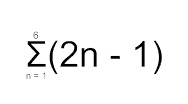
Tarkoittaa siis summaa kuudelle ensimmäiselle termille lukujonossa, jonka yleinen jäsen saadaan kaavalla an = 2n - 1. Lukunon ensimmäinen jäsen a1 = 1 ja kuudes jäsen a6 = 11.
Kaavaan sijoitettuna summaksi saadaan Σ = 6 · [(1 + 11) : 2] = 6 · 6 = 36
Summan voisi esittää myös muodossa 1 + 3 + 5 + 7 + 9 + 11 = 36
Summalausekkeet ovat käytännöllisiä silloin, kun yhteenlaskettavia on suuri määrä.
Esimerkki. Laske summa
------------------------------------------------------------------------------------------------------------------------------------------
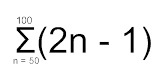
4.5 Geometrinen lukujono
Geometrisessa lukujonossa kahden peräkkäisen termin suhde eli jakolasku antaa tuloksena aina saman luvun, joka on lukujonolle ominainen suhdeluku q. Huomaa, että suhde määritetään jakolaskulla
Esimerkiksi lukujonossa 2, 4, 8, 16, 32, 64...
suhdeluku q = 2, koska
64 : 32 = 2
16 : 8 = 2
4 : 2 = 2
------------------------------------------------------------------------------------------------------------------------------------------
Geometrisen lukujonon seuraava jäsen saadaan siis aina kertomalla lukujonon jäsen suhdeluvulla q.
Yleisesti voidaan kirjoittaa seuraavasti:
a1
a2 = a1 · q
a3 = a2 · q = a1 · q · q = a1 · q2
a4 = a3 · q = a1 · q3
a5 = a4 · q = a1 · q4
· ·
· ·
· ·
an = a1 · qn - 1
Yleinen termi voidaan määrittää, kun tiedetään lukujonon ensimmäinen jäsen ja suhdeluku q. Huomaa, että suhdeluvun q potenssina käytetään yhtä pienempää lukua kuin on etsityn termin järjestysluku.
------------------------------------------------------------------------------------------------------------------------------------------
an : an - 1
Esimerkiksi lukujonossa 2, 4, 8, 16, 32, 64...
suhdeluku q = 2, koska
64 : 32 = 2
16 : 8 = 2
4 : 2 = 2
------------------------------------------------------------------------------------------------------------------------------------------
Geometrisen lukujonon seuraava jäsen saadaan siis aina kertomalla lukujonon jäsen suhdeluvulla q.
Yleisesti voidaan kirjoittaa seuraavasti:
a1
a2 = a1 · q
a3 = a2 · q = a1 · q · q = a1 · q2
a4 = a3 · q = a1 · q3
a5 = a4 · q = a1 · q4
· ·
· ·
· ·
an = a1 · qn - 1
Yleinen termi voidaan määrittää, kun tiedetään lukujonon ensimmäinen jäsen ja suhdeluku q. Huomaa, että suhdeluvun q potenssina käytetään yhtä pienempää lukua kuin on etsityn termin järjestysluku.
------------------------------------------------------------------------------------------------------------------------------------------
4.6 Geometrinen summa
Geometrisen summan Sn = a1 + a2 + ... + an arvo voidaan laskea kaavalla
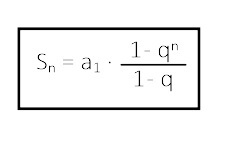Huomaa, että q ≠ 1, koska nimittäjä ei voi olla 0.
Kaavassa
* a1 on summan ensimmäinen yhteenlaskettava
* q on suhdeluku
* n on yhteenlaskettavien määrä
Kaavan johtaminen otetaan harjoitustehtävänä.
------------------------------------------------------------------------------------------------------------------------------------------
Esimerkki: laske geometrisen jono 1, 4, 16, 64,... 10 ensimmäisen termin summa käyttämällä summakaavaa.
a1 = 1
q = 4
n = 10
→ sijoitus kaavaan S10 = 1 · (1 - 410) : (1 - 4) = -1 048 575 : (-3) = 349 525
------------------------------------------------------------------------------------------------------------------------------------------
Harjoitustehtävä: laske lukujonon 5, 25, 125,... kuuden ensimmäisen termin summa.
------------------------------------------------------------------------------------------------------------------------------------------
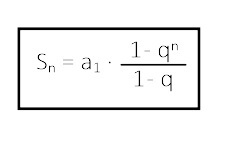Huomaa, että q ≠ 1, koska nimittäjä ei voi olla 0. Kaavassa
* a1 on summan ensimmäinen yhteenlaskettava
* q on suhdeluku
* n on yhteenlaskettavien määrä
Kaavan johtaminen otetaan harjoitustehtävänä.
------------------------------------------------------------------------------------------------------------------------------------------
Esimerkki: laske geometrisen jono 1, 4, 16, 64,... 10 ensimmäisen termin summa käyttämällä summakaavaa.
a1 = 1
q = 4
n = 10
→ sijoitus kaavaan S10 = 1 · (1 - 410) : (1 - 4) = -1 048 575 : (-3) = 349 525
------------------------------------------------------------------------------------------------------------------------------------------
Harjoitustehtävä: laske lukujonon 5, 25, 125,... kuuden ensimmäisen termin summa.
------------------------------------------------------------------------------------------------------------------------------------------